Articles about data structures: When I was writing a blog, I felt a bit strenuous at the level of expression. If the overall expression of the article is not clear enough, I beg readers to forgive me. I have tried my best.

1. Heap introduction

1. The nature of the heap

For the graph theory foundation of binary tree, please refer to: http://t.csdn.cn/Nv325 http://t.csdn.cn/Nv325Qingcai friendly reminder: Basic concepts are very important for understanding the implementation and use of heaps

The essence of the heap is a complete binary tree mapped on the sequential storage structure (array) in memory ( the complete binary tree is the logical structure of the heap ).

Heap diagram:

The data in the node is stored in the array element space of the corresponding subscript

2. Classification of heaps

Two types of heaps:

Big root heap: the value stored in the parent node of any substructure in the big root heap is greater than the value stored in its left and right child nodes (that is, any connected path satisfies descending order from top to bottom )

Small root heap: the value stored in the parent node of any substructure in the small root heap is smaller than the value stored in its left and right child nodes (that is, any connected path satisfies ascending order from top to bottom )

2. The implementation of the heap (taking the small root heap as an example)

1. Two sets of important conclusions about binary trees :

The number parent of any parent node of the heap and the number leftchild of its left child node satisfy the following relationship:

The number parent of any parent node of the heap and the number rightchild of its right child node satisfy the following relationship:

For the derivation and analysis of these two important conclusions, please refer to Qingcai’s blog: http://t.csdn.cn/Nv325 http://t.csdn.cn/Nv325

2. The physical storage structure framework of the heap (simple construction of dynamic arrays)

The heap is a complete binary tree (size root) stored on the array , so before implementing the heap, we first build a simple dynamic array as the physical storage structure framework:

Structure for maintaining dynamic arrays:

typedef int HPDataType;   //堆元素类型
typedef struct Heap
{
	HPDataType* arry;     //堆区内存指针
	size_t size;          //堆元素个数
	size_t capacity;      //数组的空间容量
}HP;

The basic operation interface declaration of the heap:

//维护堆的结构体的初始化接口
void HeapInit(HP* php);


//销毁堆的接口
void HeapDestroy(HP* php);


//堆元素的打印接口
void HeapPrint(HP* php);


//判断堆是否为空(堆中有无元素)的接口
bool HeapEmpty(HP* php);


//返回堆中元素个数的接口
size_t HeapSize(HP* php);


//返回堆顶元素(即编号为0的元素)的接口
HPDataType HeapTop(HP* php);

Implementation of the basic interface:

//堆结构体的初始化接口
void HeapInit(HP* ptrheap)
{
	assert(ptrheap);
	ptrheap->arry = NULL;
	ptrheap->capacity = 0;
	ptrheap->size = 0;

}


//销毁堆的接口
void HeapDestroy(HP* ptrheap)
{
	assert(ptrheap);
	free(ptrheap->arry);
	ptrheap->arry = NULL;
	ptrheap->capacity = 0;
	ptrheap->size = 0;
}


//堆的打印接口
void HeapPrint(HP* ptrheap)
{
	assert(ptrheap);
	size_t tem = 0;
	for (tem = 0; tem < ptrheap->size; ++tem)
	{
		printf("%d->", ptrheap->arry[tem]);

	}
	printf("END\n");
}



//判断堆是否为空的接口
bool HeapEmpty(HP* ptrheap)
{
	assert(ptrheap);
	return (0 == ptrheap->size);
}


//返回堆元素个数的接口
size_t HeapSize(HP* ptrheap)
{
	assert(ptrheap);
	return ptrheap->size;
}


//返回堆顶元素的接口
HPDataType HeapTop(HP* ptrheap)
{
	assert(!HeapEmpty(ptrheap));
	return ptrheap->arry[0];
}

A simple diagram of the memory layout when the main function builds the heap:

The array on the heap area is applied for by calling malloc in the heap element insertion interface (we have not yet implemented the heap element insertion interface)

The above is the construction of the storage framework of the heap in memory, but the core interface of the heap is the insertion and deletion interface of heap elements

3. Heap element insertion interface (take small root heap as an example)

Overview of the construction process of the heap: Insert elements one by one to the end of the heap (insert the end of the element into the array) , and each time an element is inserted , it goes up layer by layer (layer in the sense of binary tree) through the adjustment algorithm of the heap ( child nodes and parent nodes) The size of the node is compared, and if the nature of the small root heap is not satisfied, the value is exchanged ) Adjust the position of the element in the heap to maintain the data structure of the small root heap .

Algorithm process diagram:

Starting from a heap with 0 nodes , we will adjust the position of the element in the heap according to the nature of the small root heap ( through the element upward adjustment algorithm ) to maintain the data structure of the small root heap . This is how we insert an element at the end. The basic idea to build a heap .

Detailed explanation of the idea of building a heap :

Obviously, after inserting element 6 at the end of the heap, the structure of the small root heap is destroyed ( 6 is smaller than its parent node 20 and does not satisfy the nature of the small root heap ) ( you can compare the size of the child node with the parent node know whether the structure of the heap has been destroyed ) , so we need to adjust the element 6 layer by layer to the upper layer of the binary tree ( the sub-steps of each adjustment are adjusted from the child node to the parent node )

The parent node (element 20 , node number 3 ) of node 8 ( element 6 ) at the end of the heap can be found through the numbering relationship between the child node and the parent node in the substructure of the tree

Next, the elements are adjusted layer by layer (the value of the child node and the parent node are exchanged) to restore the data structure of the small root heap:

The first step of upward adjustment : compare the node whose tail is inserted into the end of the heap (No. 8 node, value 6) with its parent node (No. 3 node, value 20), the parent node is greater than the child node Point , exchange the value of the parent node and the child node (Swap in the figure below is the element value exchange interface):

The second step of upward adjustment : After exchanging the values of node 8 and node 3, we found that the small heap structure is still not established , so repeat the above adjustment process , and continue to adjust element 6 to the parent node position of the upper layer , repeat iterations until the small heap structure is restored or element 6 is transferred to the top of the heap :

It can be seen that after another adjustment, element 6 reaches node 1. At this time, node 1 is greater than node 0 , the data structure of the small heap is restored , and the adjustment process is terminated.

At the same time, it is not difficult to analyze that any upward adjustment process of elements at the end of the heap is carried out on the connected path from the end of the heap to the top element of the heap ( the order of magnitude of the path length is logk ) (k is the total number of nodes in the current tree)) :

According to the above analysis, we can design an algorithm interface for upward adjustment of heap tail elements :

Interface header: arry is a pointer to the first address of the array , and child is the number of the element at the end of the heap ( the node number is also the array subscript of the element )
void AdjustUp(HPDataType* arry, size_t child);
Algorithm interface for upward adjustment of heap tail elements:
//元素交换接口
void Swap(HPDataType* e1, HPDataType* e2)
{
	assert(e1 && e2);
	HPDataType tem = *e1;
	*e1 = *e2;
	*e2 = tem;
}



//小堆元素的向上调整接口
void AdjustUp(HPDataType* arry, size_t child)  //child表示孩子结点的编号
{
	assert(arry);
	size_t parent = (child - 1) / 2;    //算出父结点的数组下标(堆编号)
	while (child > 0)			        //child减小到0时则调整结束(堆尾元素已调到堆顶)
	{
		if (arry[child] < arry[parent]) //父结点大于子结点,则子结点需要上调以保持小堆的结构
		{
			Swap(arry + child, arry+parent);
			child = parent;				//将原父结点作为新的子结点继续迭代过程
			parent = (child - 1) / 2;	//算出父结点的数组下标(堆编号)
		}
		else
		{
			break;						//父结点不大于子结点,则堆结构恢复,无需再调整
		}
	}
}
The details that need to be paid attention to in the algorithm interface for upward adjustment of heap tail elements :

There are two termination conditions for the tuning loop:

One is that the adjusted element is transferred to the top of the heap (that is, when child=0)

When the adjusted element is larger than its parent node, the data structure of the small heap is restored , and break terminates the loop

With this interface, we can design the heap element insertion interface:

HP * ptrheap is a pointer to a heap structure , and x is the value of the element to be inserted
void HeapPush(HP* ptrheap, HPDataType x)
// 插入一个小堆元素的接口
// 插入x以后，保持其数据结构依旧是小堆
void HeapPush(HP* ptrheap, HPDataType x)        //ptrheap是指向堆结构体的结构体指针
{
	assert(ptrheap);
	if (ptrheap->capacity == ptrheap->size)	    //数组容量检查,容量不够则扩容
	{
		size_t newcapacity = (0 == ptrheap->capacity) ? 4 : 2 * ptrheap->capacity;
        //注意容量为0则将堆区数组容量调整为4
		HPDataType* tem = (HPDataType*)realloc(ptrheap->arry, newcapacity*sizeof(HPDataType)); //空间不够则扩容
		assert(tem);             //检查扩容是否成功
		ptrheap->arry = tem;     //将堆区地址赋给结构体中的指针成员
		ptrheap->capacity = newcapacity; //容量标记更新
	}
	ptrheap->arry[ptrheap->size] = x;			//元素尾插入堆
	ptrheap->size++;


	//将尾插的元素进行向上调整以保持堆的数据结构(复用元素向上调整接口)
	AdjustUp(ptrheap->arry, ptrheap->size - 1); //根据完全二叉树的结构特点可知堆尾元素                
                                                //在二叉树中编号为size-1
}
This interface can complete the insertion of a heap element (and the data structure of the small root heap can be maintained after each insertion )

If we want to create a small root heap with n elements, just call the HeapPush interface n times

4. Heap element insertion interface test

Now we try to use the HeapPush interface to build a small heap of six elements, and print the heap to observe its logical structure:
Main function code:
int main ()
{
    HP hp;              //创建一个堆结构体
	HeapInit(&hp);      //结构体初始化
	HeapPush(&hp, 1);   //调用堆元素插入接口建堆
	HeapPush(&hp, 5);
	HeapPush(&hp, 0);
	HeapPush(&hp, 8);
	HeapPush(&hp, 3);
	HeapPush(&hp, 9);
	HeapPrint(&hp);     //打印堆元素
}
Let's observe the logical structure of the printed small root heap:

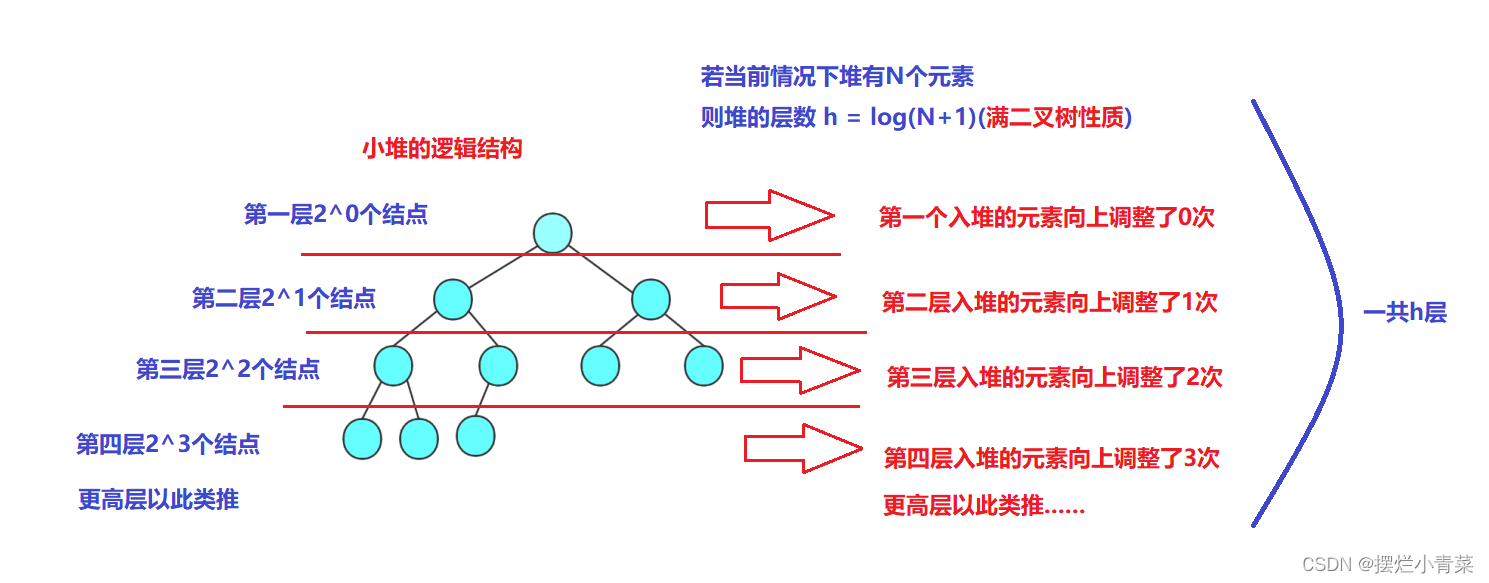
5. Time complexity analysis of heap element insertion interface building heap (heap building time complexity)

Suppose now we want to call the HeapPush interface to create a small heap of N elements ( call the HeapPush interface N times )

Note: We only focus on the worst case of time complexity (that is, assuming that each element inserted into the end of the heap is adjusted up to the top of the heap along the connected path )

When analyzing the time complexity of building a heap, we regard the heap as a full binary tree ( a full binary tree is a special complete binary tree ), that is to say, when the heap has N elements, the number of layers of the heap h=log(N+1) (the Logarithms are based on 2, and in computer science we generally don't care about the base of logarithms )

Next, we sum up the number of upward adjustments of all elements to get the time complexity of building a heap with the HeapPush interface :

The above formula can be summed and calculated by using the dislocation subtraction method :

Therefore, it can be obtained that the time complexity of using the heap element insertion interface ( heap element upward adjustment algorithm ) to build a heap ( to create a small root heap with N elements ) is: O(NlogN);

6. Heap element deletion interface (also take the small root heap as an example)

The heap element deletion we are discussing refers to: delete the top data of the heap

The basic idea of deleting the elements at the top of the heap :

First exchange the top element with the heap tail element , and then reduce the size ( the member variable that records the number of heap elements ) in the structure maintaining the heap by one ( equivalent to removing the heap tail element )

However, after the original heap tail element is swapped to the heap top position , the data structure of the small root heap will be destroyed , so we need to adjust the heap top element downward :

Graphical demonstration of downward adjustment of top elements:

It is also not difficult to analyze that any downward adjustment process of the top elements of the heap is carried out on the connected path from the top of the heap to the tail of the heap ( the order of magnitude of the path length is logk ) (k is the total number of nodes in the current tree)) :

Through algorithm analysis , we can design a heap element downward adjustment algorithm interface :

arry is a pointer to the first address of the memory heap array , size is the total number of nodes in the heap , and parent is the number of the node to be adjusted in the heap;
void AdjustDown(HPDataType* arry,size_t size,size_t parent)
Heap element downward adjustment algorithm interface implementation:
//元素交换接口
void Swap(HPDataType* e1, HPDataType* e2)
{
	assert(e1 && e2);
	HPDataType tem = *e1;
	*e1 = *e2;
	*e2 = tem;
}

//小堆元素的向下调整接口
void AdjustDown(HPDataType* arry,size_t size,size_t parent)
{
	assert(arry);
	size_t child = 2 * parent + 1;   //确定父结点的左孩子的编号
	while (child < size)			 //child增加到大于或等于size时说明被调整元素被调整到了叶结点上,调整过程结束
	{
		if (child + 1 < size && arry[child + 1] < arry[child])//确定左右孩子中较小的孩子结点
		{
			++child;   //条件成立说明右孩子较小,child更新为右孩子编号
		}
		if ( arry[child] < arry[parent])//父结点大于子结点,则父结点需要下调以保持小堆的结构
		{
			Swap(arry + parent, arry + child);//父子结点进行值交换
			parent = child;				      //将原来的子结点作为新的父结点继续迭代过程
			child = 2 * parent + 1;		      //继续向下找另外一个子结点
		}
		else
		{
			break;						//父结点不大于子结点,则小堆结构成立,无需继续调整
		}
	}
}
Note some details and boundary conditions of the algorithm interface :

child<size indicates that the adjusted element has been adjusted to the position of the leaf node, and the adjustment process ends

In the algorithm interface, we only designed a child variable to record the number of the child node of the current parent node , and then compare the size of the left and right children by arry[child + 1] < arry[child] to determine whether the child is the left child The number is still the number of the right child (note that the child+1<size judgment statement is to determine whether the right child exists)
With the heap element downward adjustment algorithm interface, we can implement the heap top data deletion interface:
//删除堆顶元素
void HeapPop(HP* ptrheap)
{
	assert(ptrheap);
	Swap(ptrheap->arry, ptrheap->arry + ptrheap->size - 1); //交换堆顶与堆尾元素
	ptrheap->size--;										//删除堆尾元素
	AdjustDown(ptrheap->arry, ptrheap->size, 0);    //将堆顶元素进行向下调整以保持堆的数据结构
}
Note: In the parameter transfer of the AdjustDown interface, ptrheadp->size refers to the total number of heap elements . Since we want to adjust the top elements of the heap downward , the adjusted node number passed in is 0
Each time this interface is called, a heap top data can be deleted ( and the data structure of the small root heap can be maintained ):

7. Heap element deletion interface test

We first call the HeapPush interface 6 times to create a small heap of six elements , and then call the HeapPop interface 6 times to delete the top elements of the heap one by one ( every time a heap top data is deleted, the heap is printed once , so as to observe the heap after each deletion of the heap top data) data structure ).
int main ()
{
    HP hp;
	HeapInit(&hp);
	HeapPush(&hp, 1);
	HeapPush(&hp, 5);
	HeapPush(&hp, 0);
	HeapPush(&hp, 8);
	HeapPush(&hp, 3);
	HeapPush(&hp, 9);
	HeapPrint(&hp);

	HeapPop(&hp);
	HeapPrint(&hp);
	HeapPop(&hp);
	HeapPrint(&hp);
	HeapPop(&hp);
	HeapPrint(&hp);
	HeapPop(&hp);
	HeapPrint(&hp);
	HeapPop(&hp);
	HeapPrint(&hp);


	HeapDestroy(&hp);

}
Observe the data structure (logical structure) of the small root heap:

It can be seen that the data structure of the small root heap is maintained during the process of deleting the top data one by one

8. Time complexity analysis of the process of deleting the top data of the heap one by one (time complexity analysis of heap deletion)

Assuming that there is a small root heap with N elements , we delete the top data one by one until the heap is empty .

Now let's analyze the time complexity of this process (we also analyze the binary tree as a full binary tree ):

Also we consider the worst case of time complexity : that is, after each call to the heap element deletion interface , the elements swapped to the top of the heap are adjusted down to the leaf nodes along the connected path

Analysis: Assuming that the height of the heap is h , the number of summary points N of the full tree is: 2^h - 1.
It should be noted that the number of nodes in the hth layer (the last layer) of the full tree is: 2^( h-1)

Therefore, the number of nodes in the last layer of the full tree accounts for half of the number of summary points in the tree

Therefore, if we delete all the nodes in the first h-1 layer of the full tree , the height of the new tree formed by the last layer of nodes is roughly h-1:

This also means that the total height of the tree will hardly change during the process of deleting the first h-1 layer nodes :

Therefore, it can be obtained that in the process of deleting all nodes in the first h-1 layer of the full tree , each element that is exchanged to the top of the heap must be adjusted log(N+1) times downwards, and then delete the first h-1 of the full tree In the process of all nodes in the layer , the total number of loop statement executions in the downward adjustment algorithm is about :

Then, for the new tree (the number of layers is h-1 layer) composed of the last layer (h-th layer) nodes of the original tree, we can do a similar analysis ( that is, first delete the first h-2 layer nodes , get A new tree composed of its h-1th layer nodes ), recursively go down in this way until the tree is deleted:

From this, it can be obtained that in the process of deleting the top data of the heap one by one until the heap is emptied, the total execution times of the loop statement in the downward adjustment algorithm of the heap elements is estimated as :

The sum of the polynomials to the big-order asymptotic notation results in O(NlogN).

The time complexity analysis of the process of deleting the top data of the heap one by one until the heap is emptied is: O(NlogN)

9. Overview of the implementation code of the heap (taking the small root heap as an example)

Header files for interface and struct type declarations:

#pragma once
#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
#include <stdbool.h>
#include <time.h>

//实现小堆

typedef int HPDataType;
typedef struct Heap
{
	HPDataType* arry;
	size_t size;
	size_t capacity;
}HP;


//堆的初始化接口
void HeapInit(HP* php);
//销毁堆的接口
void HeapDestroy(HP* php);
//堆的打印接口
void HeapPrint(HP* php);
//判断堆是否为空的接口
bool HeapEmpty(HP* php);
//返回堆元素个数的接口
size_t HeapSize(HP* php);
//返回堆顶元素的接口
HPDataType HeapTop(HP* php);


void Swap(HPDataType* pa, HPDataType* pb);
//堆元素向上调整算法接口
void AdjustUp(HPDataType* a, size_t child);
//堆元素向下调整算法接口
void AdjustDown(HPDataType* a, size_t size,size_t parent);
// 插入元素x以后，保持数据结构是(大/小)堆
void HeapPush(HP* php, HPDataType x);
// 删除堆顶的数据后,保持数据结构是(大/小)堆
void HeapPop(HP* php);

Implementation of each heap operation interface:

#include "heap.h"


//堆的初始化接口
void HeapInit(HP* ptrheap)
{
	assert(ptrheap);
	ptrheap->arry = NULL;
	ptrheap->capacity = 0;
	ptrheap->size = 0;

}
//销毁堆的接口
void HeapDestroy(HP* ptrheap)
{
	assert(ptrheap);
	free(ptrheap->arry);
	ptrheap->arry = NULL;
	ptrheap->capacity = 0;
	ptrheap->size = 0;
}


//堆的打印接口
void HeapPrint(HP* ptrheap)
{
	assert(ptrheap);
	size_t tem = 0;
	for (tem = 0; tem < ptrheap->size; ++tem)
	{
		printf("%d->", ptrheap->arry[tem]);

	}
	printf("END\n");
}



//判断堆是否为空的接口
bool HeapEmpty(HP* ptrheap)
{
	assert(ptrheap);
	return (0 == ptrheap->size);
}


//返回堆元素个数的接口
size_t HeapSize(HP* ptrheap)
{
	assert(ptrheap);
	return ptrheap->size;
}




//返回堆顶元素的接口
HPDataType HeapTop(HP* ptrheap)
{
	assert(!HeapEmpty(ptrheap));
	return ptrheap->arry[0];
}





//元素交换接口
void Swap(HPDataType* e1, HPDataType* e2)
{
	assert(e1 && e2);
	HPDataType tem = *e1;
	*e1 = *e2;
	*e2 = tem;
}



//小堆元素的向上调整接口
void AdjustUp(HPDataType* arry, size_t child)  //child表示孩子结点的编号
{
	assert(arry);
	size_t parent = (child - 1) / 2;
	while (child > 0)						   //child减小到0时则调整结束
	{
		if (arry[child] < arry[parent])        //父结点大于子结点,则子结点需要上调以保持小堆的结构
		{
			Swap(arry + child, arry+parent);
			child = parent;				//将原父结点作为新的子结点继续迭代过程
			parent = (child - 1) / 2;	//继续向上找另外一个父结点
		}
		else
		{
			break;						//父结点不大于子结点,则堆结构任然成立,无需调整
		}
	}
}

// 插入一个小堆元素的接口
// 插入x以后，保持其数据结构依旧是小堆
void HeapPush(HP* ptrheap, HPDataType x)
{
	assert(ptrheap);
	if (ptrheap->capacity == ptrheap->size)	//容量检查,容量不够则扩容
	{
		size_t newcapacity = (0 == ptrheap->capacity) ? 4 : 2 * ptrheap->capacity;
		HPDataType* tem = (HPDataType*)realloc(ptrheap->arry, newcapacity * sizeof(HPDataType));
		assert(tem);
		ptrheap->arry = tem;
		ptrheap->capacity = newcapacity;
	}
	ptrheap->arry[ptrheap->size] = x;			//先尾插一个元素
	ptrheap->size++;
	//将尾插的元素进行向上调整以保持堆的数据结构
	AdjustUp(ptrheap->arry, ptrheap->size - 1); //根据完全二叉树的结构特点可知尾插进数组的元素在二叉树中编号为size-1
}



//小堆元素的向下调整接口
void AdjustDown(HPDataType* arry,size_t size,size_t parent)
{
	assert(arry);
	size_t child = 2 * parent + 1;   //确定父结点的左孩子的编号
	while (child < size)			 //child增加到大于或等于size时则调整结束
	{
		if (child + 1 < size && arry[child + 1] < arry[child]) //确定左右孩子中较小的孩子结点
		{
			++child;
		}
		if ( arry[child] < arry[parent])//父结点大于子结点,则子结点需要上调以保持小堆的结构
		{
			Swap(arry + parent, arry + child);
			parent = child;				//将原子结点作为新的父结点继续迭代过程
			child = 2 * parent + 1;		//继续向下找另外一个子结点
		}
		else
		{
			break;						//父结点不大于子结点,则堆结构任然成立,无需调整
		}
	}
}


//删除堆顶元素
void HeapPop(HP* ptrheap)
{
	assert(ptrheap);
	Swap(ptrheap->arry, ptrheap->arry + ptrheap->size - 1); //交换堆顶与堆尾元素
	ptrheap->size--;										//删除堆尾元素
	AdjustDown(ptrheap->arry, ptrheap->size, 0);			//将堆顶元素进行向下调整以保持堆的数据结构
}

We only need to change the size comparison symbol of the child-parent node value in the interface of the small-root heap to adjust the heap elements up and down to the greater-than sign to realize the large-root heap

10. Epilogue

The core of this article: complete the construction and deletion of the heap through the up and down adjustment algorithm interface of the heap elements (and analyze the time complexity of the process)

The heap element adjustment algorithm interface will be directly used in subsequent heap sorting and TopK problems

The efficiency of the heap comes from the following mathematical ideas: use the exponentially expanded data structure model to implement the logarithmic connected path traversal algorithm , thereby reducing the time complexity of sorting and searching (it has to be said that the creation of the predecessors is really impossible. match)

Data Structure: Implementation of Heap and Time Complexity Analysis of Heap Construction

foreword