Y: "This question has the difficulty of the Blue Bridge Cup Group A national competition or the difficulty of the ACM silver medal"
After two afternoons of research, I finally figured out the details
Title description:
Given a sequence A of length N, it is required to divide the sequence into several segments, and to minimize the sum of "the maximum value of all numbers in each segment" under the premise that "the sum of all numbers in each segment" does not exceed M. Try to calculate this minimum.
The first line of the input format contains two integers N and M. The second line contains N integers representing the complete sequence A.
The output format outputs an integer representing the result. If the result does not exist, output −1.
Data range 0≤N≤105 , 0≤M≤1011 , the number in sequence A is non-negative and does not exceed 106
Input example: 8 17 2 2 2 8 1 8 2 1
Sample output: 12
The range of N is 1E5 and the time complexity should be controlled at O(NlogN) level
Violent enumeration triple cycle time complexity O(N^3 ) level
Far greater than 10^8 Consider how to optimize
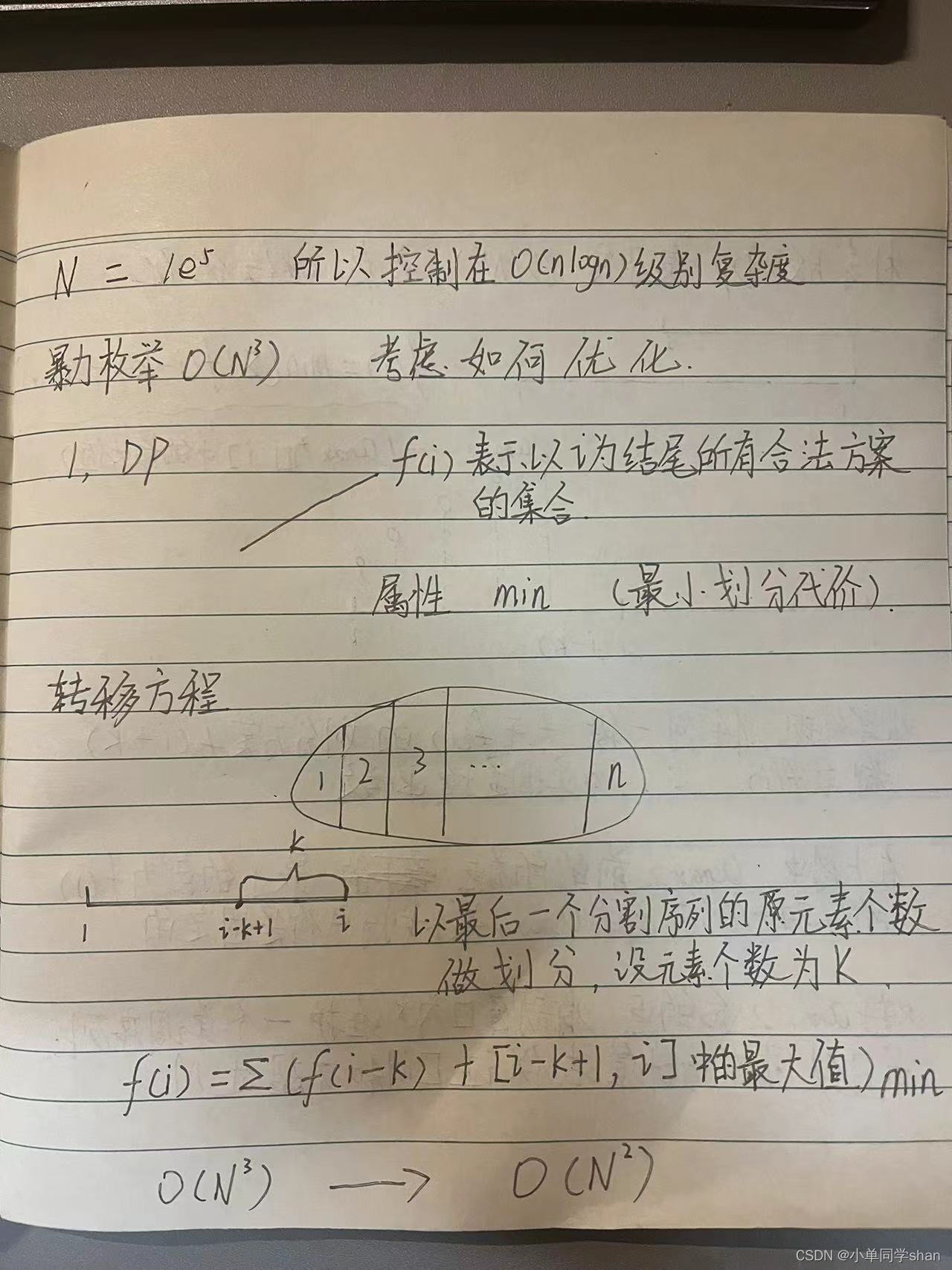
1,DP
State definition:
f(i): Represents the set of all legal division schemes ending with i
Attribute: minimum partition cost
state transition:
Divide by the number of elements in the last split sequence, assuming that the number of elements in the last split sequence is k
Then f(i) = min(Σ(f(i - k) + amax)) ; Note: amax represents the largest number in the last split sequence
2. Double pointer + monotonic queue

As shown in the figure above, it is observed that for any division scheme larger than f(i) , a division scheme corresponding to it can be found in f(i), and the division cost is strictly >= f(i), so f (i) is a monotonically increasing function
Because f is monotonically increasing, so for the maximum value amax in the last interval, when the left endpoint j of the last interval is to the left of amax at this time, we only need to consider one point for transfer: one point on the left.
In this way, in the non-worst case, it is not necessary to enumerate each k for state calculation, but to enumerate the maximum value of each available interval.
When the left end point J of the interval reaches the current amax, the meaning of f(j) is - the division scheme ending with J
At the time of transfer, since our transfer equation is - f(j) + the division cost amax of the last segment , then amax is not updated as the division cost of the last segment. At this time, we need to find another amax
According to this property, it is conceivable to use a monotonic queue to maintain a sliding window monotonic sequence
Then the queue head is a currently available amax . When the left endpoint J exceeds amax, this element pops up, and the next element is still the maximum value of the currently available interval.
Note: This is the problem of maintaining the maximum value of the sliding window in a monotonic queue. What is maintained in the queue is (maximum value, second largest value, second largest value....) I won’t go into too much detail here
The double-pointer algorithm can guarantee that the interval sum does not exceed m
But at this time our time complexity is still O(N^2) in the worst case
Because in the worst case, there may still be a monotonic sequence of n elements, for each sliding window, it is necessary to enumerate each point in the monotonic sequence to update the minimum value, and consider how to continue the optimization.
Now to recap what we did:
After the DP state transition equation is introduced, for each f(i), it needs to be enumerated during the transition—the number of elements K of all the last legal division schemes. The time complexity of this algorithm is O(N^2) above
Since f(i) is a monotonically increasing function , for each available amax, only the smallest point needs to be considered
So I thought of using a monotonic queue to maintain a maximum value of a sliding window , and the head of the queue is the maximum value amax currently available .
But in the worst case, there may still be n monotonic sequences. In this case, it is equivalent to no optimization.
3.multiset
At this time, our requirement becomes to maintain the minimum value in an interval for state calculation.
If the minimum value in this set can be dynamically maintained , there is no need to enumerate each amax when transferring.
To dynamically maintain the minimum value in an interval, many data structures can be implemented. For example: heap, balanced tree
It can be directly maintained by set in STL (implemented by balanced tree), and synchronized with the sliding window. At most one element can be added and one element can be deleted at a time. The complexity is O(log) level;
In this way, even in the worst case, we don't need to enumerate every possible amax (up to n),
In this way, it is optimized from O(N^2) to O(NlogN) ;
If you can persist in seeing this, I will give you a thumbs up!
Code:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<set>
using namespace std;
const int N = 1e5 + 10;
typedef long long LL;
LL f[N];
int q[N];
LL a[N];
int n;
LL m;
multiset<LL> s;
void remove(LL k)//这样写的目的是维护集合中,防止把多个相同值都删掉
{
auto x = s.find(k);
s.erase(x);//用迭代器只删除当前位置
}
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++ )
{
cin >> a[i];
if(a[i] > m) //出现大于m的值,一定不存在合法划分方案
{
puts("-1");
return 0;
}
}
int hh = 0,tt = -1;
LL sum = 0;
for(int i = 1, j = 1; i <= n; i ++)//双指针维护区间不超过m的滑动窗口
{
sum += a[i];
while(sum > m)
{
sum -= a[j ++ ];//j为左端点
if(hh <= tt && q[hh] < j)//如果队列中最左边的位置小于滑动窗口左端点 删除掉
{
if(hh < tt) remove(f[q[hh]] + a[q[hh + 1]]);
hh ++;
}
}
while(hh <= tt && a[q[tt]] <= a[i])
/*单调队列 如果队尾元素小于等于当前元素 一定不会作为最大值更新,删除掉*/
{
if(hh < tt) remove(f[q[tt - 1]] + a[q[tt]]);
tt --;
}
q[ ++ tt ] = i;//队尾加入当前元素
if(hh < tt) s.insert(f[q[tt - 1]] + a[q[tt]]);//hh < tt 保证队列中至少两个点
f[i] = f[j - 1] + a[q[hh]];
/*注意:j是区间左端点,包括在最后一个区间内的,计算的时候需要-1才是上一个区间,否则的话不符合转移方程.这一步是以第一个amax也就是单调队列中的第一个元素来计算f(i),set中维护的是从第二个amax作为最后一段最大值开始的,这步我想了很久才想通,特别注意下*/
if(s.size()) f[i] = min(f[i],*s.begin());
}
printf("%lld", f[n]);
return 0;
}
tip:
j is the left endpoint of the interval maintained by the double pointer , so it is included in the last interval,
Then when the state is transferred, -1 is required to be the end position of the previous interval, otherwise it does not conform to the transfer equation.
What is maintained in the set is the situation after starting with the second amax as the maximum value of the last segment
The first amax is calculated as the minimum f() corresponding to the second amax , because f is monotonous
In other words, the minimum f() corresponding to each possible amax is at the position of the previous amax
f (the position of the previous amax) represents the set of all division schemes that end at the position of the previous amax
Then this value cannot be used as the maximum value in the division scheme of the last paragraph .
I thought about this step for a long time before I figured it out, pay special attention!
