Today's final supplement and summary of RS coding, we can review and answer the questions raised in the first part more completely!
For the coding matrix of RS, we can obtain the list [Qm, Rm-1, Rm-2, ...... R2, R1, R0] by comprehensive division , but we also need to replace Qm with the original data [ D0,D1.....Dn], that is, finally generate [D0,D1,D2....Dn, Rm-1,Rm-2,.......R2,R1,R0], this is the is the last data we can save, the specific code is as follows:
def rs_encode_msg(msg_in, nsym):
gen = rs_generator_poly(nsym)
# Initialize msg_out with msg_in value and suffix with ecc bytes, padded with 0.
msg_out = [0] * (len(msg_in) + len(gen)-1)
msg_out[:len(msg_in)] = msg_in
# Synthetic division main loop
for i in range(len(msg_in)):
coef = msg_out[i]
if coef != 0: # avoid log(0) undefined errors
for j in range(1, len(gen)): # Since the first position of the polynomial is 1, (1^1==0) it can be skipped
msg_out[i+j] ^= gf_mul(gen[j], coef) # equivalent to msg_out[i+j] += gf_mul(gen[j], coef)
# After division, msg_out contains quotient msg_out[:len(msg_in)] and remainder msg_out[len(msg_in):].
#RS code only uses the remainder, so we use the original information to cover the quotient to get the complete code.
msg_out[:len(msg_in)] = msg_in
return msg_out
The corresponding RS code is still as follows:
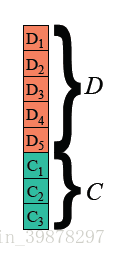
The matrix C is the remainder obtained by the RS code [R2, R1, R0], and the matrix D is the original data [D1, D2, D3, D4, D5]. Now we have gone from Galois field to generator polynomial to comprehensive division and then I have learned a lot of knowledge about the RS coding principle in the BCH code, so let's go back to the first part and answer the thinking that we ignored at the time, why do [D0, D1, D2....Dn, Rm-1, Rm -2,.......R2,R1,R0] What about this matrix?
We can get from the above code that we add [0,0,0] to the suffix of the original data [D1,D2,D3,D4,D5] to become [D1,D2,D3,D4,D5,0,0,0] , then we get [Q1,Q2,Q3,Q4,Q5,R2,R1,R0] by synthetic division (where the list [Q1,Q2,Q3,Q4,Q5] represents the polynomial of the quotient), then we'll use this code :
#RS code only uses the remainder, so we use the original information to cover the quotient to get the complete code.
msg_out[:len(msg_in)] = msg_in
So we turn the encoding into [D1, D2, D3, D4, D5, R2, R1, R0], so what's the use of compiling it like this?
Here we must always combine what was said before! Remember how we got the surplus when we came into contact with the BCH code?
def qr_check_format(fmt):
g = 0x537 # = 0b10100110111 in python 2.6+
for i in range(4,-1,-1):
if fmt & (1 << (i+10)): # Determine if it is 1
fmt ^= g << i
return fmt
The final fmt is the remainder obtained by dividing the original fmt of the input by the generator polynomial. Using this code, we can apply it to checking errors. The code for checking errors is as follows (the fmt below has nothing to do with the fmt above, and there is no connection):
encoded_format = (format<<10) ^ qr_check_format(format<<10)
We regard the divisor generator polynomial as G, the dividend (fmt<<10) as F, the function of the function qr_check_format (format<< 10 ) is to regard F/G, the obtained quotient as Q, and the remainder as R, this function finally The output is R. So the formula (format<< 10 ) ^ qr_check_format(format<< 10 ) can be translated into the final encoding encoded_format = F ^ R
We know the relation F = Q*G +R, so for F^R = ( Q*G +R )^R, since XOR^ can represent both addition and subtraction in Galois Field, we get F^R = ( Q*G +R )^R = Q*G +R -R = Q*G
Q is the quotient and we can ignore it, but G represents the generator polynomial, which means that the final encoded encoded_format can be divisible by the generator polynomial G!
But don't we put the RS code again? Why is this code mentioned?
This is the most ingenious RS encoding process! Sexiest! It's a crazy place to call ah ah ah ah!
During the RS encoding process, we added the original fmt suffix to the list [0,0,...0], and found this thing familiar? !
That's right! We can fully think of the previous encoded_format = (format<< 10 ) ^ qr_check_format(format<< 10 ) , this format<<10 refers to a left shift of 10 bits relative to the binary, followed by zero padding, whether this is the same as the original fmt Does the suffix plus the list [0,0,...0] have the same purpose? ? ! ! We will get the new fmt with the remainder of the comprehensive division [ Rm-1,Rm-2,.......R2,R1,R0] , and finally we will cover the original fmt with [Q1,Q2,Q3.. The part of the quotient of .Qn, Rm-1,Rm-2,.......R2,R1,R0], get the RS code [D1,D2,D3...Dn,Rm-1,Rm-2 ,......R2,R1,R0].
Combined with explanation, RS code = [D1,D2,D3...Dn, Rm-1,Rm-2,.......R2,R1,R0] = [D1,D2,D3... Dn,0,0,...0] ^ [Rm-1,Rm-2,.......R2,R1,R0] = ( fmt+suffix [0,0,..0] ) ^ Find remainder ( fmt + suffix [0,0,..0] )
It corresponds to the above encoded_format = (format<< 10 ) ^ qr_check_format(format<< 10 ) one by one! ! ! Crazy call for the author who invented this code! ! ! !
Finally, the RS code we get is Q(x)*G(x), that is, the RS code is divisible by the generator polynomial G(x)! This is why we want to become this matrix, because this feature will be very useful in the decoding part of the RS code later!
The RS coding part is over, and we will talk about RS decoding tomorrow.