#1378 : Network flow 2 Max-flow min-cut theorem
describe
Xiao Hi: In the Hiho session last week, we initially explained the concept of network flow and conventional solutions. Do you still remember the content, Xiao Ho?
Little Ho: I remember! The network flow is given a graph G=(V, E), and the source point s and the sink point t. Each edge e(u,v) has capacity c(u,v). The maximum flow problem of network flow is to solve the maximum flow from s to t.
Xiao Hi: What is the solution to this problem?
Xiao Ho: The basic idea of solving the network flow is to find an augmentation path and continuously update the residual network. Until no new augmentation path is found, the flow obtained at this time is the maximum flow of the network.
Xiao Hi: Yes, it seems that you remember it very well.
Little Ho: Hey, but I have a question here, why did you find the maximum flow when you couldn't find the augmenting path?
Xiao Hi: This time, I will solve your doubts. First of all, we will start with the cutting of network flow.
For a network flow graph G=(V,E), its cut is defined as a point division method: all points are divided into two parts S and T=VS, where the source point s∈S, the sink point t ∈T.
For a cut (S, T), we define the net flow f(S, T) as the sum of the flows across the cut (S, T) , namely:
f(S,T) = Σf(u,v) | u∈S,v∈T
For example (this example is taken from Introduction to Algorithms):
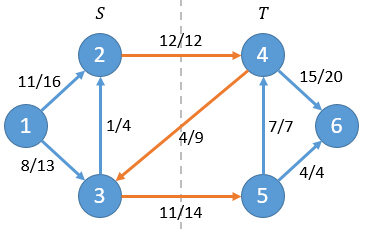
Net flow f = f(2,4)+f(3,4)+f(3,5) = 12+(-4)+11 = 19
At the same time, we define the capacity of the cut C(S, T) as the sum of the capacity of all edges from S to T , namely:
C(S,T) = Σc(u,v) | u∈S,v∈T
Also in the above example, the capacity of its cut is:
c(2,4)+c(3,5)=12+14=26
Small Ho: That is to say, when calculating the net flow f(S,T) of the cut (S,T), there may be a reverse flow such that f(u,v)<0, and the capacity C(S,T) must be non- negative number.
Xiao Hi: You are right. In fact, the net flow f(S, T) for any cut is always equal to the flow f of the network flow. For example, in the above example, we change the way of cutting:
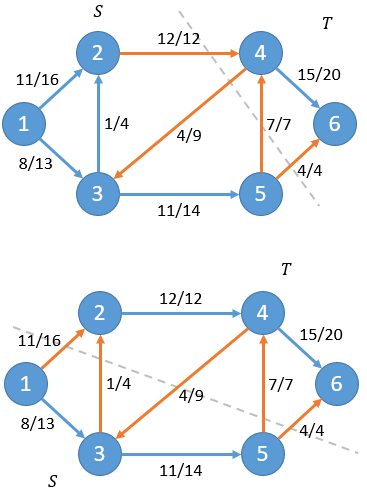
It can be calculated that the net flow f(S,T) is still equal to 19 for both cases.
An intuitive explanation is: According to the definition of network flow, only source s will generate traffic and sink t will receive traffic. Therefore, for any point u other than s and t, its net flow must be 0, that is, Σ(f(u,v))=0. The flow of the source point s will eventually reach the sink point t through the edge of the cut (S, T), so the flow f of the network flow is equal to the static flow f(S, T) of the cut.
The strict proof is as follows:
f(S,T) = f(S,V) - f(S,S) The flow from S to T is equal to the flow from S to all nodes minus the flow from S to the internal nodes of S f(S,T) = f(S,V) Since the flow existing between nodes inside S must have a corresponding reverse flow, f(S,S)=0 f(S,T) = f(s,V) + f(S-s,V) Then divide S set into source point s and other nodes belonging to S f(S,T) = f(s,V) Since other nodes other than the source point s will not generate flow, f(Ss,V)=0 f(S,T) = f(s,V) = f
So f(S, T) is equal to the flow from the source s, which is the flow f of the network.
Xiao Ho: If you understand it simply, that is to say, the net flow f(S, T) of any cut is equal to the flow f of the current network .
Xiao Hi: That's it. For any cut, the net flow f(S, T) must be less than or equal to the capacity C(S, T) of the cut. That is, for any flow f of the network, the capacity C(S, T) of any cut must be less than or equal to.
Among all possible cuts, there is a cut with the smallest capacity, which we call the minimum cut .
This minimum cut constrains the upper bound on the flow f of a network, so we have:
For any network flow graph, its maximum flow must be less than or equal to the minimum cut.
Xiao Ho: But what does this have to do with Augmented Road?
Xiao Hi: Next is the key point. Using the knowledge mentioned above, we can derive a max-flow min-cut theorem :
For a network flow graph G=(V, E) with source s and sink t, then the following three conditions are equivalent: 1. The flow f is the maximum flow of the graph G 2. There is no augmentation path in the residual network Gf 3. For a certain cut (S, T) of G, then f = C(S, T)
First prove that 1 => 2 :
We use counter-evidence to assume that flow f is the maximum flow of graph G, but there is also an augmenting path p in the residual network whose flow is fp. Then we have flow f'=f+fp>f. This contradicts that f is the maximum flow.
Then prove that 2 => 3 :
Suppose there is no augmenting path in the residual network Gf, so there is no path from s to t in the residual network Gf. We define the S set as: the points that s can reach in the current residual network. Also define T=VS. At this point (S, T) constitutes a cut (S, T). And for any u∈S, v∈T, there is f(u,v)=c(u,v). If f(u,v)<c(u,v), then Gf(u,v)>0, s can reach v, which contradicts that v belongs to T. So there is f(S,T)=Σf(u,v)=Σc(u,v)=C(S,T).
Finally prove that 3 => 1 :
Since the upper bound of f is the minimum cut, when f reaches the capacity of the cut, it will obviously reach the maximum value, so f is the maximum flow.
This explains why when the augmenting path cannot be found, the maximum flow must be obtained.
Little Ho: So it is, I understand.
enter
Line 1: 2 positive integers N,M. 2≤N≤500, 1≤M≤20,000.
Lines 2..M+1: 3 integers u,v,c(u,v) in each line, representing an edge (u,v) and its capacity c(u,v). 1≤u, v≤N, 0≤c(u, v)≤100.
The default source point is 1 and the sink point is N in a given graph. There may be duplicate edges.
output
Line 1: 2 integers AB, A represents the capacity of the minimum cut, and B represents the number of points in the set of minimum cuts S of the given graph G.
Line 2: B space-separated integers representing the point numbers of the S set.
If there are multiple minimum cuts, any solution can be output.
- sample input
-
6 7 1 2 3 1 3 5 2 4 1 3 4 2 3 5 3 4 6 4 5 6 2
- Sample output
-
5 4 1 2 3 5
Analysis: The S set in the question is the set containing the source point s, first run the maximum flow (dinic), find the residual network
and then bfs layering, at this time, the points that can be traversed from the source point are all S Concentrated points, because the edge of the minimum cut must be full of flow, that is, the residual flow is 0. View Code
View Code#include<cstdio> #include<cstring> #include<algorithm> #include<queue> #define INF 999999999 using namespace std; int map[502][502]; int N,M; int dis[502],p[502]; int bfs() { memset(dis,-1,sizeof(dis)); dis[1]=0; queue<int> q; q.push(1); while(!q.empty()) { int u=q.front(); q.pop(); for(int i=1;i<=N;i++) if(dis[i]==-1&&map[u][i]>0) { dis [i] = dis [u]+ 1 ; q.push(i); } } if(dis[N]>0) return 1; return 0; } int dfs(int cur,int m) { if(cur==N) return m; int f,res=0; for(int i=1;i<=N;i++) { if(dis[i]==dis[cur]+1&&map[cur][i]>0&&(f=dfs(i,min(m,map[cur][i])))) { map[cur][i]-=f; map[i][cur]+=f; res+=f; m-=f; if(!m) break; } } if(res) return res; dis[cur]=-1; return 0; } intmain () { scanf("%d%d",&N,&M); for(int i=0;i<M;i++) { int s,t,c; scanf("%d%d%d",&s,&t,&c); map[s][t]+=c; } int ans=0,res; while(bfs()) while(res=dfs(1,INF)) ans+=res; int cnt=0; for(int i=1;i<=N;i++) if(dis[i]!=-1) p[cnt++]=i; printf("%d %d\n",ans,cnt); for(int i=0;i<cnt;i++) printf("%d ",p[i]); printf("\n"); return 0; }
