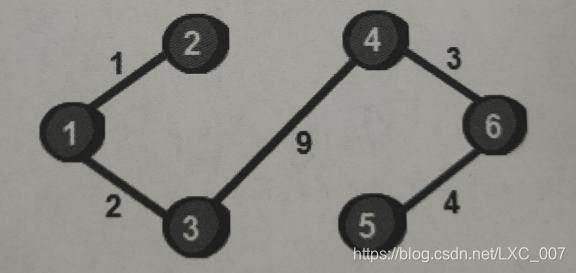
镖局每到一个新地方开展业务,都需要对运镖途中的绿林好汉进行打点。好说话的打点费就比较低,不好说话的打点费就比较高。现在已知城镇地图如下,顶点是城镇编号,边上的值表示这条道路上打点绿林好汉需要的银子数。
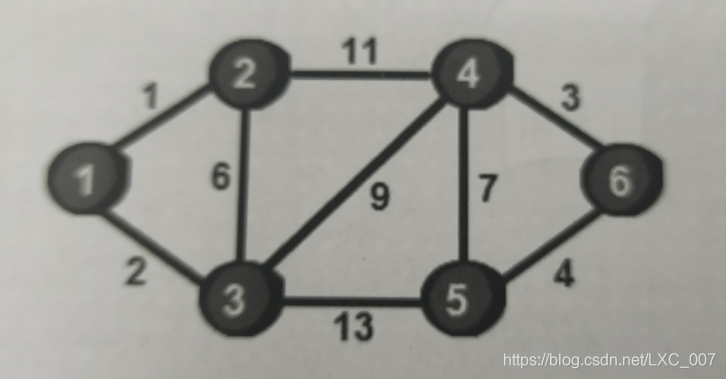
数据给出如下:
6 9
2 4 11
3 5 13
4 6 3
5 6 4
2 3 6
4 5 7
1 2 1
3 4 9
1 3 2
第一行有两个数n和m,n表示有n个城市,m表示有m条道路。接下来的m行,每行形如“a b c”用来表示一条道路,意思是城市a到城市b需要花费的银子数是e。
镖局现在需要选择一些道路进行疏通,使镖局可以到达任意一个城镇,要求是花的银子越少越好。换句话说,镖局的要求就是用最少的边让图连通,那么至少需要n-1条边。如果一个连通无向图不包含回路,那么这就是一棵树,其实这里就是要求一个图的最小生成树。需要特别说明以下的是,我们在这里只讨论无向图的最小生成树。
那么问题的关键就是:如何选出这n-1条边,使边的长度之和最短呢?
既然要求是让边的总长度之和最短,我们自然可以想到首先选择最短的边,然后选择次短的边……知道选择了n-1条边为止。这就需要先对所有的边按照权值进行从小到大排序,然后从最小的开始选,一次选择每一条边,知道选择了n-1条边让整个图连通为止。将上图中的所有边排序之后如下:
1 2 1
1 3 2
4 6 3
5 6 4
2 3 6
4 5 7
3 4 9
2 4 11
3 5 13
选择过程如下:



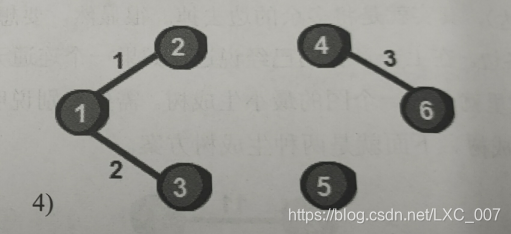
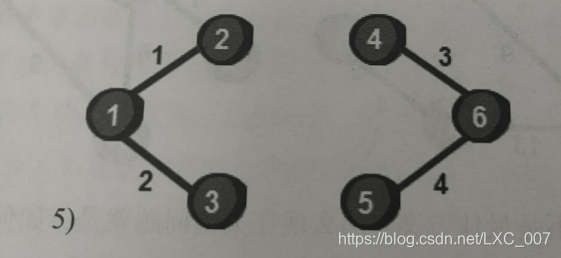
选用2 3 6这条边时我们发现此时2号顶点和3号顶点已经连通了,不再需要这条边了。如果加上这条边就会形成回路,那就不是树了,因此需要跳过这条边。
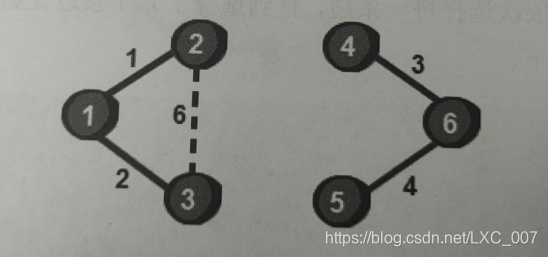
接下来是4 5 7这条边,同理这条边也不能用。
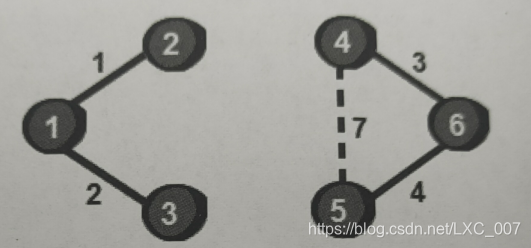
最终选用了n-1条边,图已经连通,算法结束,如下:
回顾刚才的算法,比较难于实现的是:**判断两个顶点是否已连通。**这一点我们可以使用深搜或广搜来解决,但这样效率太低。我们有更好的选择,那就是用并查集。将所有顶点放入一个并查集中,判断两个顶点是否连通,只需判断这两个顶点是否在同一集合(即是否有共同的祖先)即可。这样时间复杂度仅为O(logN)。
这个算法叫Kruskal算法。
总结
首先按照边的权值进行从小到大排序,每次从剩余的边中选择权值较小且边的两个顶点不再同一集合内的边(就是不会产生回路的边),加入到生成树中,直到加入了n-1条边为止。
代码
#include <stdio.h>
#include <iostream>
using namespace std;
struct edge{
int u;
int v;
int w;
};//为了方便排序,这里创建了一个结构体来存储边的关系
struct edge e[10];//数组的大小要根据实际情况来设置,至少要比m的最大值大1
int n, m;
int f[10] = {
0}, sum = 0, count = 0;
void quicksort(int left, int right){
int i, j;
struct edge t;
if(left > right) return ;
i = left;
j = right;
while(i != j){
//顺序很重要,要先从右边开始找
while(e[j].w >= e[left].w && i < j) j--;
//再从左边开始找
while(e[i].w <= e[left].w && i < j) i++;
//交换
if(i < j){
t = e[i];
e[i] = e[j];
e[j] = t;
}
}
//最终将基准数归位,将left和i互换
t = e[left];
e[left] = e[i];
e[i] = t;
quicksort(left, i - 1);//继续处理左边的,这里是一个递归的过程
quicksort(i + 1, right);//继续处理右边的,这里是一个递归的过程。
return ;
}
int findfather(int v){
if(f[v] == v) return v;
else{
//这里是压缩路径
f[v] = findfather(f[v]);
return f[v];
}
}
//并查集合并两个子集的函数
int merge(int v, int u){
int t1, t2;
t1 = findfather(v);
t2 = findfather(u);
if(t1 != t2){
f[t2] = t1;
return 1;//没有连通返回1
}
return 0;//连通了返回2
}
//请从此处开始阅读程序,从主函数开始阅读程序是一个好习惯
int main(){
int i;
//读入边n和m,n表示顶点个数,m表示边的条数
cin >> n >> m;
//读入边,这里用一个结构体来存储边的关系
for (int i = 1; i <= m; ++i){
cin >> e[i].u >> e[i].v >> e[i].w;
}
//按照权值从小到大对边进行快速排序
quicksort(1, m);
//并查集初始化
for (int i = 1; i <= n; ++i)
f[i] = i;
//Kruskal算法核心语句
for (int i = 1; i <= m; ++i){
//开始从小到大枚举每一条边
//判断一条边的两个顶点是否已经连通,即判断是否已在同一个集合中
if(merge(e[i].u, e[i].v)){
//如果目前尚未连通,则选用这条边
count ++;
sum = sum + e[i].w;
}
if(count == n - 1)//直到选用了n - 1条边之后退出循环
break;
}
printf("%d", sum);//打印结果
cout << endl;
return 0;
}
可以输入以下数据进行验证:
6 9
2 4 11
3 5 13
4 6 3
5 6 4
2 3 6
4 5 7
1 2 1
3 4 9
1 3 2
运行结果是:
19
时间复杂度
对边进行快速排序的时间复杂度是O(MlogM),在m条边中要找出n - 1条边是O(MlogN),所以Kruskal算法的时间复杂度为O(MlogM + MlogN)。通常M要比N大很多,因此O(MlogN)可以省略,因此最终的时间复杂度为O(MlogM)。