table of Contents
1. The longest continuous increasing sequence
2. The longest ascending subsequence
3. The number of the longest increasing subsequence
5. The longest continuous sequence
Here are some topics related to increasing subsequences. Some topics will have optimal solutions, but the main focus here is on the practice of dynamic programming , so only dynamic programming or some general methods are written.
Before introducing these topics, first distinguish between what is a subsequence and what is a substring
Subsequence: The subsequence is not continuous, such as the sequence [4, 6, 5] is [1, 2, 4, 3, 7, 6, 5] a subsequence
Substring: The substring is continuous
1. The longest continuous increasing sequence
Input: [1,3,5,4,7]
Output: 3
Explanation: The longest continuous increasing sequence is [1,3,5], and the length is 3.
Although [1,3,5,7] is also an ascending subsequence, it is not continuous because 5 and 7 are separated by 4 in the original array.
This question is about increasing sequence, but the requirement is continuous, so it is actually seeking increasing substring
class Solution:
def findLengthOfLCIS(self, nums: List[int]) -> int:
if not nums:
return 0
if len(nums) == 1:
return 1
dp = [1]*len(nums) #代表连续递增序列的长度
for i in range(1,len(nums)):
if nums[i]>nums[i-1]: #如果后一个元素大于前一个元素,那长度+1
dp[i] = dp[i-1]+1
return max(dp) # 找出最大的那个数就是长度,不能是dp[-1],dp[-1]代表的是以最后一个元素结尾是最长连续递增序列,但是最后一个并不一定是最大的数。2. The longest ascending subsequence

Use dynamic programming to do it, define the dp array to represent the length of the subsequence, dp[i] represents any element before the i-th element as the starting point, and the length of the ascending subsequence to the end of the i-th element , initialized to 1 , Which means that each element can at least become a subsequence individually, and the length is 1 at this time.
After traversing to each element nums[i], traverse the elements nums[j] in [0-i] from the beginning. If nums[i]>nums[j], then nums[i] can be accessed To the back of the nums[j] element, that is, dp[i] = dp[j] + 1
So the recursive equation is dp[i] = max(dp[i],dp[j]+1) , in the end, we still find max(dp) instead of dp[-1]
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
if not nums:
return 0
dp=[1]*len(nums)
for i in range(len(nums)):
for j in range(i):
if nums[i]>nums[j]:
dp[i] = max(dp[i],dp[j]+1)
return max(dp)If the inner loop of this question traverses from 0 every time, there are actually many repeated traversals, so the inner loop can use the dichotomy to find the first number greater than num[i], and then replace it with num[i], not much to say, the code is as follows:
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
res = []
for num in nums:
if not res or num>res[-1]:
res.append(num)
else:
l=0
r=len(res)-1
while l<r:
mid = (l+r)//2
if res[mid]<num:
l = mid+1
else:
r = mid
res[l]=num
return len(res)3. The number of the longest increasing subsequence

This question is very similar to the one above, except that there is an additional count of the number of the longest increasing subsequence
class Solution:
def findNumberOfLIS(self, nums: List[int]) -> int:
if not nums:
return 0
dp = [1]*len(nums)
count = [1]*len(nums)
temp = 1
res = 0
for i in range(1,len(nums)):
for j in range(i):
if nums[i]>nums[j]:
if dp[j]+1>dp[i]:
dp[i] = dp[j]+1
count[i] = count[j]
elif dp[i] == dp[j]+1:
count[i]+=count[j]
# temp = max(temp,dp[i])
temp = max(dp)
for i in range(len(nums)):
if dp[i] == temp:
res += count[i]
return resWhen dp[j]+1> dp [i], it means that the new length is found for the first time, which is dp[j]+1. At this time, count[i] = count[j], indicating nums[i] the longest ending The combination of increasing subsequences is equal to the nums[j] current combination
When dp[j]+1 = dp [i], it means that the increasing sequence of this length has been found once, then count[i]+=count[j],the number of existing combinations plus count [j] is the total combination Number
The last traversal is to find the longest length, and its corresponding count is the result
You can also use a tree array for this question. Currently, the ability is limited, so I don’t know how to use a tree array. Skip
4. Increasing subsequence

This problem is no longer using dynamic programming, but depth-first search, similar to backtracking. If you use the general backtracking solution, it takes too much time. The code is as follows
class Solution:
def __init__(self):
self.res = []
def findSubsequences(self, nums: List[int]) -> List[List[int]]:
def dfs(temp,start,nums):
if len(temp)>=2 and temp not in self.res:
self.res.append(temp[:])
for i in range(start,len(nums)):
if not temp or nums[i]>=temp[-1]:
temp.append(nums[i])
dfs(temp,i+1,nums)
temp.pop()
temp = []
dfs(temp,0,nums)
return self.res
It can be seen that it takes more than 6,000 milliseconds to use a collection to pruning is still taking too long, you can use a dictionary to pruning.
class Solution:
def findSubsequences(self, nums: List[int]) -> List[List[int]]:
res = []
def dfs(start, tmp):
dic = {}
if len(tmp) > 1:
res.append(tmp)
for i in range(start, len(nums)):
if dic.get(nums[i], 0):
continue
if len(tmp) == 0 or nums[i] >= tmp[-1]:
dic[nums[i]] = 1
dfs(i + 1, tmp + [nums[i]])
dfs(0, [])
return res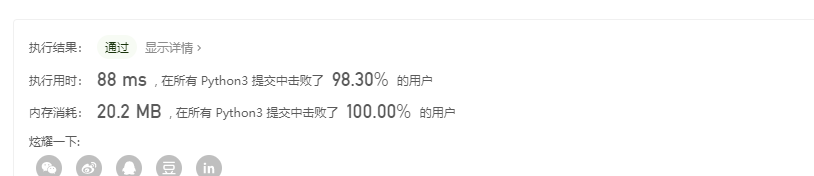
The time consuming dropped all of a sudden.
5. The longest continuous sequence
Leave it empty first, learn and check the collection and then improve it