RSA algorithm encryption and decryption knowledge collation

RSA overview

First look at the name of this encryption algorithm, it is very interesting, it is actually the name of three people. As early as 1977, three encryptionists Rivest, Shamir, and Adleman of the Massachusetts Institute of Technology proposed this encryption algorithm, and named them with the initial letters of their three surnames.
RSA can be used as asymmetric encryption. The public key and secret key are relative. This is because the information encrypted by one can be decrypted by the other. Generally, the secret key kept by yourself is the private key, and the public key is sent to the other party. Next, let us sort out the RSA algorithm. Prerequisites: Number theory related

Key generation steps

We use an example to understand the RSA algorithm. Suppose Alice wants to communicate encryptedly with Bob, how should she generate public and private keys?

The first step is to randomly select two unequal prime numbers p and q.

Alice chose 61 and 53. (In practical applications, the larger these two prime numbers, the harder it is to crack.)

In the second step, the product n of p and q is calculated.

Alice multiplied 61 and 53.

n = 61×53 = 3233

The length of n is the key length. 3233 is written as binary is 110010100001, there are 12 bits in total, so this key is 12 bits. In practical applications, the RSA key is generally 1024 bits, and 2048 bits in important occasions.

The third step is to calculate the Euler function φ (n) of n.

According to the formula:
φ (n) = (p-1) (q-1)

Alice calculated that φ (3233) is equal to 60 × 52, or 3120.

In the fourth step, an integer e is randomly selected, provided that 1 <e <φ (n), and e and φ (n) are relatively prime.

Alice is between 1 and 3120, randomly choosing 17. (In practice, 65537 is often selected.)

In the fifth step, calculate the inverse element d of e for φ (n).

The so-called "modulo inverse element" refers to an integer d, which can make ed divided by φ (n) remainder is 1.

ed ≡ 1 (mod φ (n))

This formula is equivalent to

ed - 1 = kφ(n)

Therefore, finding the inverse element d is essentially solving the following binary linear equation.

ex + φ (n) y = 1

It is known that e = 17, φ (n) = 3120,

17x + 3120y = 1

This equation can be solved by "Extended Euclidean Algorithm", and the specific process is omitted here. In short, Alice calculated a set of integer solutions as (x, y) = (2753, -15), that is, d = 2753.

At this point all calculations are complete.

The sixth step is to encapsulate n and e into a public key, and n and d into a private key.

In Alice ’s example, n = 3233, e = 17, d = 2753, so the public key is (3233,17) and the private key is (3233, 2753).

Encrypt and decrypt

(1) Public key (n, e) is used for encryption

Suppose Bob wants to send encrypted information m to Alice, he will encrypt m with Alice's public key (n, e)
. It should be noted here that m must be an integer (string can take ascii value or unicode value), and m must be less than n.

The so-called "encryption" is to calculate the following formula c:
　　

Alice ’s public key is (3233, 17), and Bob ’s m hypothesis is 65, then the following equation can be calculated:

6517 ≡ 2790 (mod 3233)

So, c equals 2790, and Bob sends 2790 to Alice.

(2) Use the private key (n, d) for decryption

After Alice received the 2790 from Bob, she decrypted it with her private key (3233, 2753). It can be proved that the following equation must be established:

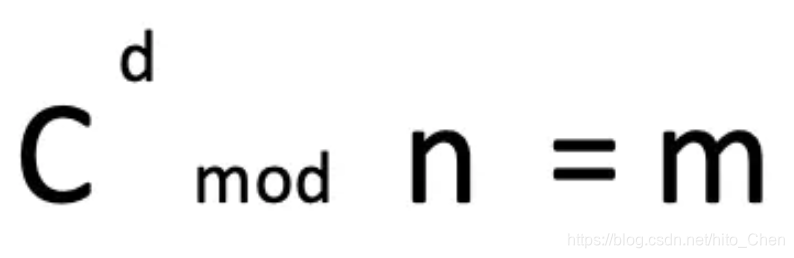
that is, the remainder of c divided by the power of d divided by n is m.

Now, c is equal to 2790, and the private key is (3233, 2753), then, Alice calculated

27902753 ≡ 65 (mod 3233)

Therefore, Alice knew that the original text before Bob's encryption was 65.

At this point, the entire process of "encryption-decryption" is completed.

RSA signature verification

The RSA cryptosystem can be used for both encryption and digital signatures. The function of RSA digital signature is introduced below.
Known public key (e, n), private key d:

1) The signature for message m is: sign ≡ m ^ d mod n
2) Verification: For message signature pair (m, sign), if m ≡ sign ^ e mod n, then sign is a valid signature of m

Reliability of RSA algorithm

Recalling the above key generation steps, a total of six numbers appear:

p q n φ (n) and d

Of these six numbers, two (n and e) are used for the public key, and the remaining four numbers are all private. The most critical one is d, because n and d form a private key, once d leaks, it is equal toPrivate key leak。

So, is it possible to derive d if n and e are known?

(1) ed≡1 (mod φ (n)). Only by knowing e and φ (n) can we calculate d.
(2) φ (n) = (p-1) (q-1). Only by knowing p and q can we calculate φ (n).
(3) n = pq. Only by factoring n can p and q be calculated.

Conclusion: If n can be factored, d can be calculated, which means that the private key is cracked.

However, factoring large integers is a very difficult thing. At present, in addition to brute force cracking, no other effective methods have been found. Wikipedia writes:

The difficulty of factoring large integers determines the reliability of the RSA algorithm. In other words, the more difficult it is to factorize a very large integer, the more reliable the RSA algorithm. As long as the key length is long enough, the information encrypted with RSA cannot actually be broken. Today, only short RSA keys can be brute-forced. As of 2008, there is no reliable way to attack the RSA algorithm in the world. The longest RSA key that is currently cracked is 768 bits.

RSA practice

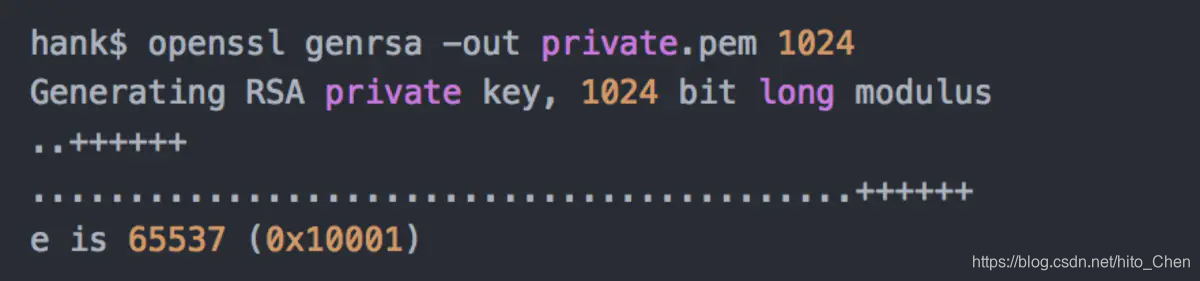
It is easy to simulate the process of RSA encryption and decryption using the openssl that comes with mac.

1) We generate a public key:
Insert picture description here
2) Extract the public key from the private key

We now have these two files:

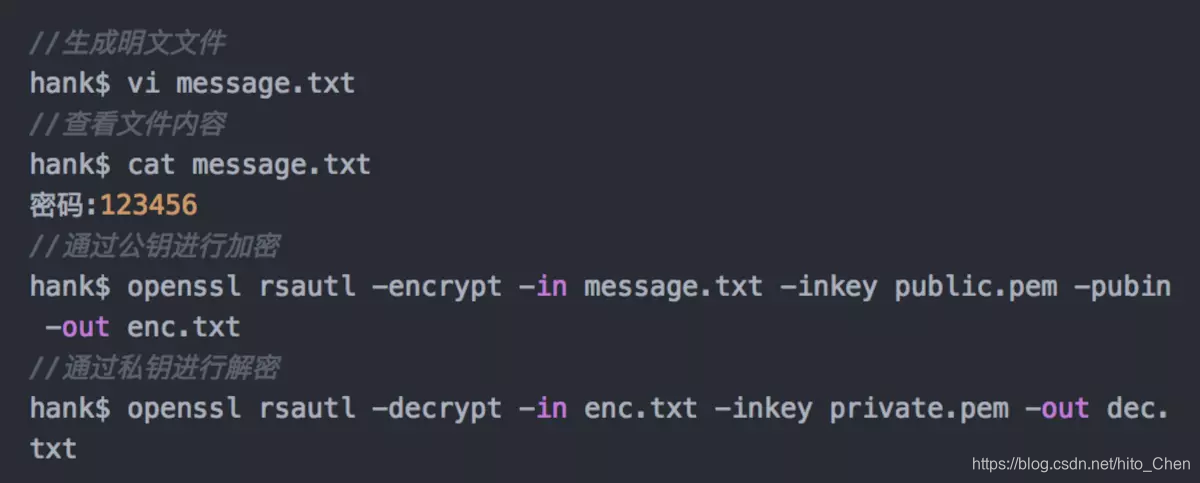
3 ､ First write a piece of clear file data, encrypt the data with the public key, and then decrypt the data with the private key