【Algorithm】 ST algorithm for interval maximum query

General Solution of Interval Maximum Value Query Problem

Interval maximum value query problem, namely RMQ (Range Minimum / Maximum Query)

Common solutions include naive algorithms- O (n) preprocessing, O (n) query, and overall complexity O (n + nq)

Line segment tree- O (nlogn) preprocessing, O (logn) query, overall complexity O ((n + q) logn)

ST algorithm- O (nlogn) preprocessing, O (1) query, overall complexity O (nlogn + q)

ST algorithm

ST algorithm is an algorithm to solve the static interval RMQ based on multiplication algorithm and dynamic programming

Ignore the naive algorithm and compare with the line tree

The advantage is that the time complexity of the query is linear, which is beneficial to many query types

The disadvantage is that it only supports the query of the static interval (the value cannot be modified after initialization), and the space complexity is greater than the line segment tree in most cases (the line tree conservative case is O (4n) , the ST algorithm is O (nlogn) )

Implementation of ST algorithm

Preprocessing section

①: Based on the multiplication algorithm, we need to preprocess the maximum value in the interval of the power of 2 from a certain position i to the second and store it

②: Assuming that there are x elements in the interval of this query, you need to return logx and round down to ensure that the algorithm O (1) is implemented, so this step is also pre-processed and stored.

Query section

Although the multiplication algorithm is used

It is easy to think that you can start from the left border L of the query

Each time log (R-L + 1) is taken down to the maximum value of the entire length interval to take the largest value from the answer (the maximum value here is the pre-processing part ①)

Update the left boundary L and continue to take it

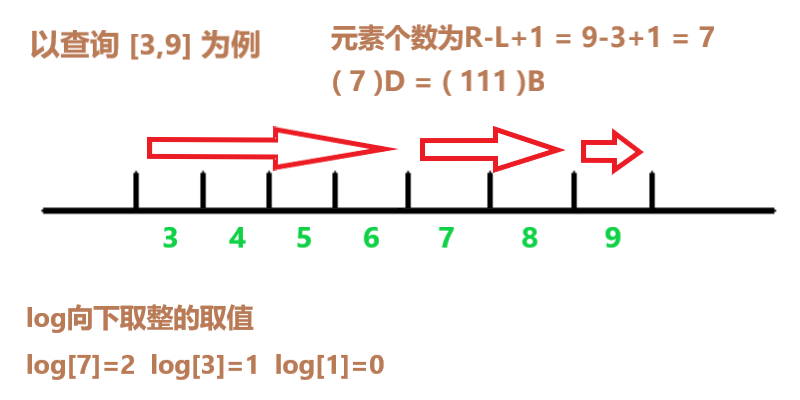
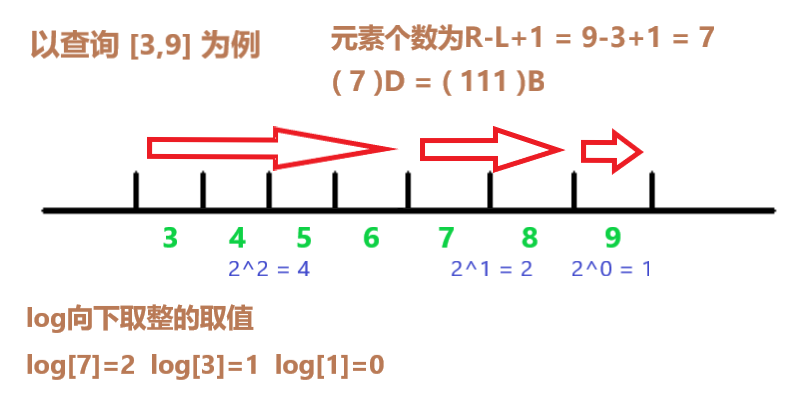
(The illustrated arrow is the update process of each L)

It can also be seen as how many steps to take based on the position of 1 after converting R-L + 1 into binary

But this approach is obviously O (logn) level

In fact, since it has been preprocessed, the maximum value in the interval from the power of multiples of 2 starting from a certain position i

Then we can log (R-L + 1) values

From L to the right, take the maximum value in the 2 ^log length interval

Then start from R and take the maximum value in the 2 ^log length interval to the left

The larger of these two maximum values ​​is the answer, and the time complexity is O (1)

It can be guaranteed that the interval taken by L to the right and the interval taken by R to the left must overlap , and will not exceed the position of the other party

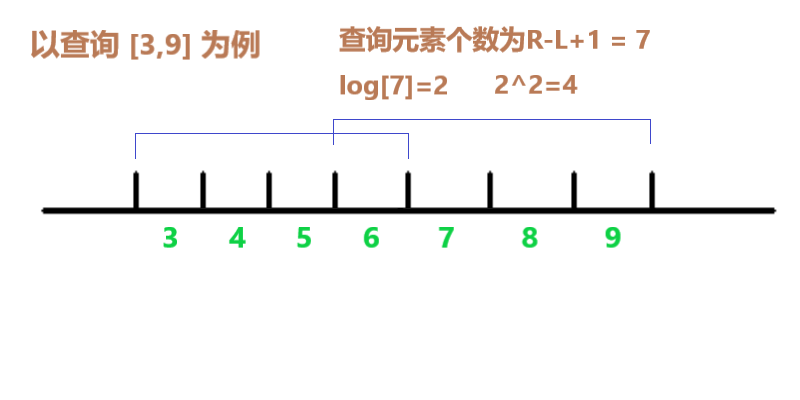
(The two line segments in the figure represent the interval taken)

Code implementation of ST algorithm

The code takes the maximum value as an example. To change to the minimum value, just change max to min.

Data storage method

const int MAXN=100050,MAXF=18;
int ar[MAXN];//原数组
int dp[MAXN][MAXF];//dp[i][j]表示从i开始往右2^j长度的区间内的最值
int LOG[MAXN];//LOG[i]=log2(i)向下取整

Ensure 2 ^MAXF-1 > MAXN, prevent cross-border

Preprocessing section

For dp array

It can be found that 2 ⁰ = 1, so the dp[i][0] = ar[i]layer 0 is processed (if there are no other conditions, you can ignore the ar array and directly read into the dp array)

Starting from j = 1, similar to the multiplication algorithm of other problems, according to the dp idea, the state transition equation can be obtained from 2 ⁱ = 2 ^i-1 + 2 ^i-1 as

dp[i][j] = max( dp[i][j-1] , dp[i+(1<<(j-1))][j-1] )

The language description is

I 2 from the start position ^j the maximum length of the interval, may be formed "from the start position i 2 ^j-1 the maximum length in the interval", "from 2 i + ^j-1 start position 2 ^j-1 within the length interval "Maximum" These two values ​​are transferred from the big

for(int i=1;i<=n;i++)
    dp[i][0]=ar[i];
for(int j=1;(1<<j)<=n;j++)//如果长度已经超过n，则没有继续处理的必要
    for(int i=1;i+(1<<(j-1))<=n;i++)//如果从i开始往右没法取2^j长度的区间，则无法继续处理
        dp[i][j]=max(dp[i][j-1],dp[i+(1<<(j-1))][j-1]);

For LOG array

According to the nature of division, the log array can be passed

log[i] = log[i/2] + 1

Transferred (log [1] = 0)

LOG[1]=0;
for(int i=2;i<=n;i++)
    LOG[i]=LOG[i/2]+1;

Query section

Enter query interval L and R

Firstly, the number of elements in the interval is R-L + 1, and the length of the corresponding ends is 2 ^{LOG [R-L + 1]}

Let d = LOG [R-L + 1]

It can be obtained that the interval from L to the right takes L as the left boundary, and the maximum value is dp [L] [d]

The left boundary of the interval from R to the left is R-2 ^d +1, then the maximum value is dp [R- (1 << d) +1] [d]

The larger of the two values ​​is the answer

scanf("%d%d",&L,&R);
d=LOG[R-L+1];
printf("%d\n",max(dp[L][d],dp[R-(1<<d)+1][d]));

Complete program (template)

Sample template question: Luogu P3865

(If there is TLE in this question, try to use fast reading, the title has been explained)

#include<bits/stdc++.h>
using namespace std;

const int MAXN=100050,MAXF=18;
int ar[MAXN];
int dp[MAXN][MAXF];
int LOG[MAXN];

int main()
{
    int n,q,L,R,d;
    scanf("%d%d",&n,&q);
    
    LOG[1]=0;
    for(int i=2;i<=n;i++)
        LOG[i]=LOG[i/2]+1;
    
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&ar[i]);
        dp[i][0]=ar[i];
    }

    for(int j=1;(1<<j)<=n;j++)
        for(int i=1;i+(1<<(j-1))<=n;i++)
            dp[i][j]=max(dp[i][j-1],dp[i+(1<<(j-1))][j-1]);

    while(q--)
    {
        scanf("%d%d",&L,&R);
        d=LOG[R-L+1];
        printf("%d\n",max(dp[L][d],dp[R-(1<<d)+1][d]));
    }

    return 0;
}

Refer to blog