Autor: Yu Fan
Hintergrund
Komplexe Raum-Zeit-Systeme, die durch partielle Differentialgleichungen modelliert werden, sind in vielen Disziplinen allgegenwärtig, beispielsweise in der angewandten Mathematik, Physik, Biologie, Chemie und Ingenieurwissenschaften. In den meisten Fällen sind wir nicht in der Lage, analytische Lösungen für PDEs zu erhalten, die zur Beschreibung dieser komplexen physikalischen Systeme verwendet werden. Daher wurden numerische Lösungsmethoden ausführlich untersucht, darunter: Finite-Elemente, Finite-Differenzen, isogeometrische Analyse (IGA) und andere Methoden. Obwohl diese traditionellen numerischen Methoden die exakte Lösung der Gleichung durch Basisfunktionen gut annähern können, gibt es immer noch einen enormen Rechenaufwand bei der Datenassimilation und der Lösung des Umkehrproblems.
In den letzten Jahren sind in einem endlosen Strom verschiedene Deep-Learning-Methoden entstanden, um Vorwärts- und Umkehrprobleme nichtlinearer Systeme zu lösen. Die Forschung zur Verwendung von DNN zur Modellierung physikalischer Systeme kann grob in die folgenden zwei Kategorien unterteilt werden: kontinuierliche Netzwerke und diskrete Netzwerke. Ein typischer Vertreter kontinuierlicher Netzwerke sind PINNs: Der Rest der PDE wird als weiche Einschränkung des neuronalen Netzwerks verwendet, und eine vollständig verbundene Schicht wird verwendet, um die Lösung der Gleichung anzunähern, und das Modell kann im kleinen Datenmaßstab oder durchgeführt werden sogar unbeschriftete abgetastete Daten. Dennoch sind PINNs häufig auf niedrigdimensionale Parametrisierungen beschränkt und werden gestreckt, wenn PDE-Systeme mit steilen Gradienten und komplexen lokalen Morphologien konfrontiert werden. Kürzlich wurde in einer kleinen Anzahl von Pilotstudien festgestellt, dass diskrete Netzwerke eine bessere Skalierbarkeit und eine schnellere Konvergenzgeschwindigkeit aufweisen als kontinuierliches Lernen. Beispielsweise kann CNN als Proxy-Modell im rechteckigen Bereich für zeitunabhängige Systeme verwendet werden Um stationäre partielle Differentialgleichungen durch Koordinatentransformation geometrisch adaptiv zu lösen, basieren die meisten neuronalen Netzwerklösungsmethoden immer noch auf datengesteuerter und vermaschter Lösung.
PhyCRNet[1], vorgeschlagen vom Team von Professor Sun Hao an der Hillhouse School of Artificial Intelligence der Renmin University of China in Zusammenarbeit mit der Northeastern University (USA) und der University of Notre Dame, ist eine unbeaufsichtigte Methode zur Lösung von PDEs in mehrdimensionalen raumzeitlichen Bereichen durch physikalisches Vorwissen und eine Faltungs-Rekursiv-Netzwerkarchitektur, die ConvLSTM (Extrahieren niedrigdimensionaler räumlicher Merkmale und Lernen der Zeitentwicklung), globale Restverbindung (strikte Abbildung von Änderungen in Gleichungslösungen auf der Zeitachse) und endliche Differenzen hoher Ordnung kombiniert Die räumlich-zeitliche Filterung (Bestimmung der Konstruktion einer Restverlustfunktion durch die Fähigkeit der erforderlichen PDE-Ableitungen) macht sie zu einer grundlegenden Lösung bei inversen Problemen und bei spärlichen und verrauschten Daten.
1. Problemdefinition
Betrachtet man mehrdimensionale nichtlineare parametrische partielle Differentialgleichungen, ist die allgemeine Form wie folgt:
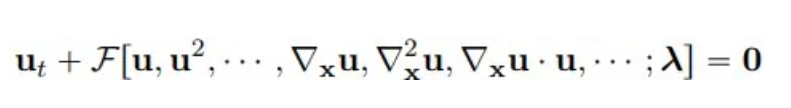
wobei u(x, t) die Lösung der Gleichung im Zeitbereich T und im Raumbereich Ω darstellt und F eine nichtlineare Funktion mit Parameter λ ist.
**2. ** Modellmethode
ConvLSTM
ConvLSTM ist ein räumlich-zeitliches Sequenz-zu-Sequenz-Lernframework, das sich von LSTM und seiner Variante der LSTM-Encoder-Decoder-Vorhersagearchitektur (die den Vorteil hat, langfristige Abhängigkeiten zu modellieren, die sich im Laufe der Zeit entwickeln) erstreckt. Im Wesentlichen wird die Speichereinheit mit den Eingabe- und Zustandsinformationen aktualisiert, auf die zugegriffen wird, und die Akkumulation und Löschung des Speichers wird durch geschickt gestaltete Kontrollgatter abgeschlossen. Basierend auf dieser Einstellung wird das Problem des Verschwindens des Gradienten gewöhnlicher wiederkehrender neuronaler Netze (RNN) gemildert. ConvLSTM erbt die Grundstruktur von LSTM (d. h. Zelleinheiten und Tore), um den Informationsfluss zu steuern, und modifiziert das vollständig verbundene neuronale Netzwerk (FC-NN), um zu berücksichtigen, dass CNN über bessere räumliche Verbindungsdarstellungsfähigkeiten verfügt und Gating-Operationen auf CNN durchführt . Als besonderer RNN-Typ kann LSTM als implizite numerische Methode zur Lösung zeitabhängiger PDE-Gleichungen verwendet werden. Das Strukturdiagramm einer einzelnen ConvLSTM-Einheit sieht wie folgt aus:
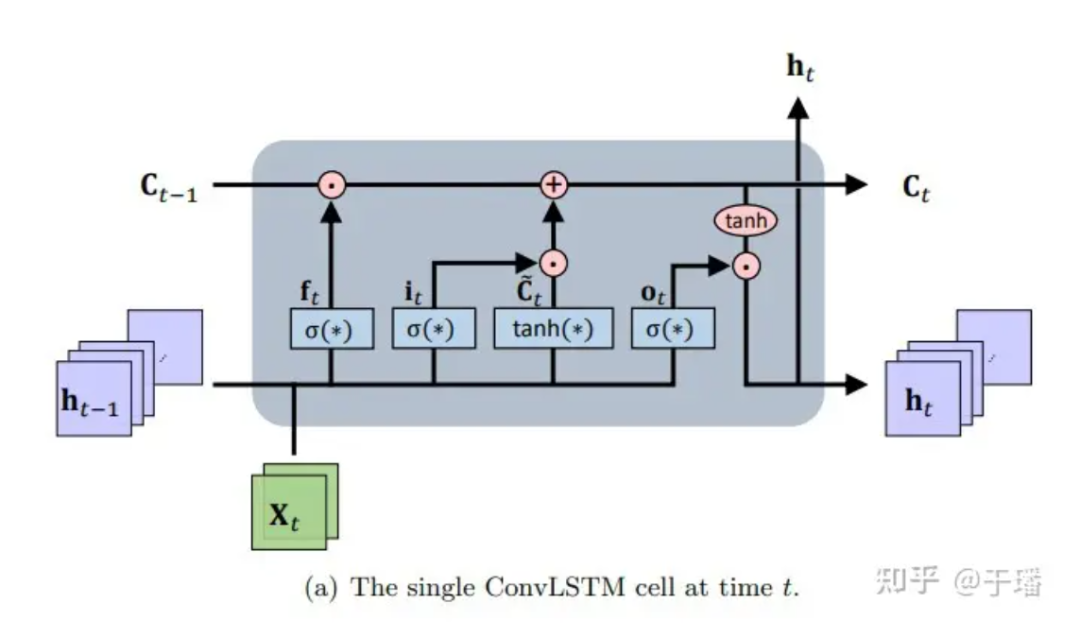Abbildung 1: Einzelne ConvLSTM-Zelle zum Zeitpunkt t
Die mathematische Darstellung der Aktualisierung einer ConvLSTM-Einheit lautet wie folgt:
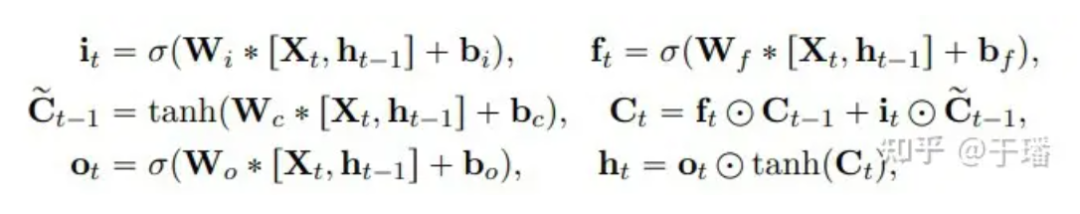
Unter diesen repräsentiert * die Faltungsoperation, ⊙ repräsentiert das Hadamard-Produkt, W ist der Gewichtsparameter des Filters und b repräsentiert den Bias-Vektor.
Pixel-Shuffle
Pixel Shuffle ist eine effiziente Subpixel-Faltungsoperation, die ein Bild mit niedriger Auflösung (LR) in ein Bild mit hoher Auflösung (HR) hochsampelt. Nehmen Sie an, dass die Abmessungen eines LR-Merkmalstensors (C) sind. Ein HR-Tensor mit den Abmessungen (C, H xr, W xr).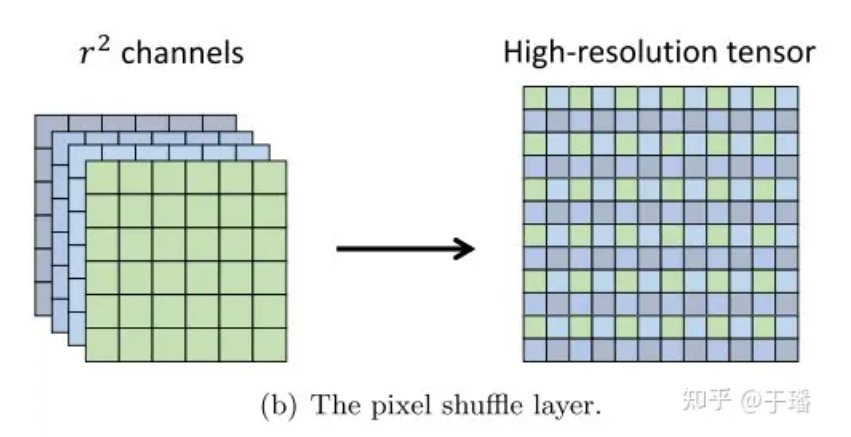 
Abbildung 2: Pixel Shuffle-Ebene
Die Effizienz von Pixel Shuffle spiegelt sich wider in: (1) Erhöhung der Auflösung nur in der letzten Faltungsschicht, wodurch die Notwendigkeit vermieden werden kann, mehr Faltungsschichten zu verwenden, um das Bild auf die Zielauflösung zu erhöhen, (2) ) In Bei allen Merkmalsextraktionsschichten vor der Upsampling-Schicht können kleinere Filter zur Verarbeitung dieser Tensoren mit niedriger Auflösung verwendet werden.
PhyCRNet
PhyCRNet besteht aus Encoder-Decoder-Modulen, Restverbindungen, autoregressiven Prozessen und einer filterbasierten Differentialmethode. Der Encoder enthält drei Faltungsschichten, um zu einem bestimmten Zeitpunkt niedrigdimensionale latente Merkmale aus der Zustandsvariablen Ui zu lernen und sie über ConvLSTM im Laufe der Zeit weiterentwickeln zu lassen. Da die Transformation für niedrigdimensionale Variablen durchgeführt wird, wird der Speicheraufwand entsprechend reduziert. Darüber hinaus können wir, inspiriert von der Vorwärts-Euler-Methode, eine globale Restverbindung zwischen der Eingabevariablen Ui und der Ausgabevariablen Ui+1 hinzufügen und den einstufigen Lernprozess als Ui+1 = Ui + δt x N ausdrücken [Ui; θ], wobei N[·] den trainierten neuronalen Netzwerkoperator darstellt und δt das Einheitszeitintervall ist. Daher kann diese rekursive Beziehung als einfacher autoregressiver Prozess angesehen werden.
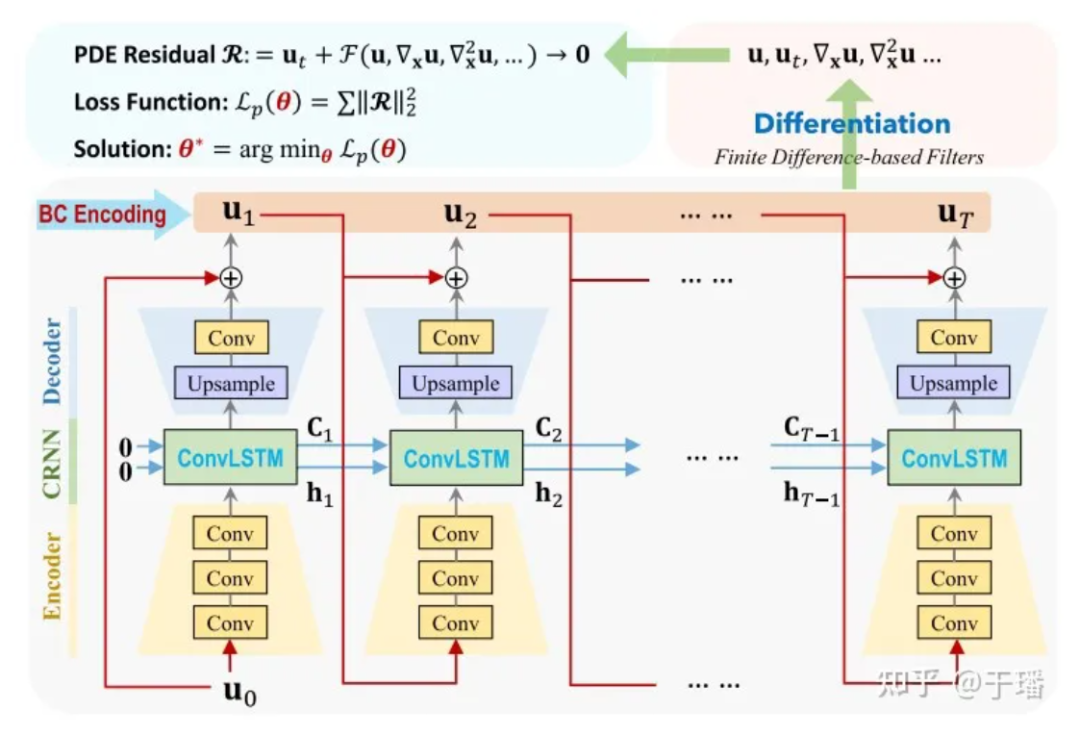Abbildung 3: PhyCRNet-Netzwerkstrukturdiagramm
Hier ist U0 die Anfangsbedingung, U1 bis UT sind die diskreten Lösungen, die vom Modell vorhergesagt werden müssen, und die Zeitentwicklung von der Eingabe bis zur Ausgabe. Im Vergleich zu herkömmlichen numerischen Methoden kann ConvLSTM ein größeres Zeitintervall verwenden. Für die Berechnung jedes Differentialterms verwenden wir einen festen Faltungskern [1], um ihre Differenzwerte darzustellen. In PhyCRNet werden Differenzterme zweiter und vierter Ordnung verwendet, um die Ableitungen von U nach Zeit und Raum zu berechnen. Um die Rechenleistung weiter zu optimieren, können wir den Encoder-Teil in einem Zyklus der Größe T überspringen, mit Ausnahme des ersten Moments jedes Zyklus. Das schematische Diagramm sieht wie folgt aus:
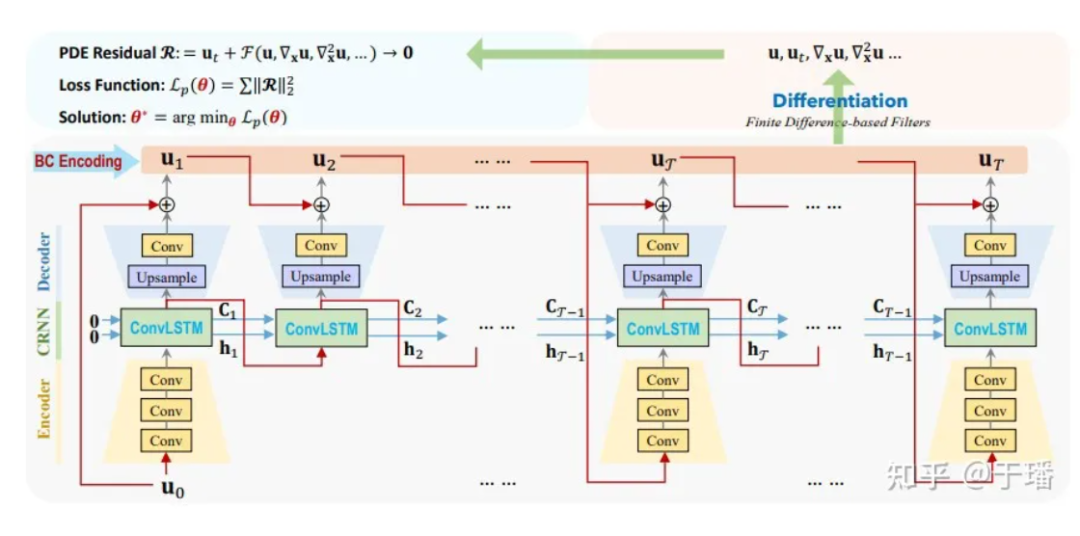Abbildung 4: Netzwerkstrukturdiagramm von PhyCRNet-s
I/BC-harte Einschränkungen
Im Vergleich zur PINNs-Methode, die physikalische Anfangsrandbedingungen als weiche Einschränkungen verwendet (ihre Residuen werden als Teil des Verlusts optimiert), verwendet PhyCRNet die Methode der harten Codierung von I/BC in das Modell (die Anfangsbedingungen werden als Eingabe U0 verwendet). von ConvLSTM und die Randbedingungen werden durch Auffüllen codiert), sodass physikalische Bedingungen keine weiche Einschränkung mehr darstellen, wodurch die Genauigkeit und Konvergenzgeschwindigkeit des Modells verbessert wird. Für Dirichlet BC können die bekannten konstanten Grenzwerte direkt als Auffüllung in den Raumbereich eingefügt werden, während für Neumann BC eine Schicht aus Geisterelementen um den Raumbereich herum hinzugefügt werden kann (Geisterelemente). durch Unterschiede während des Trainingsprozesses angenähert.
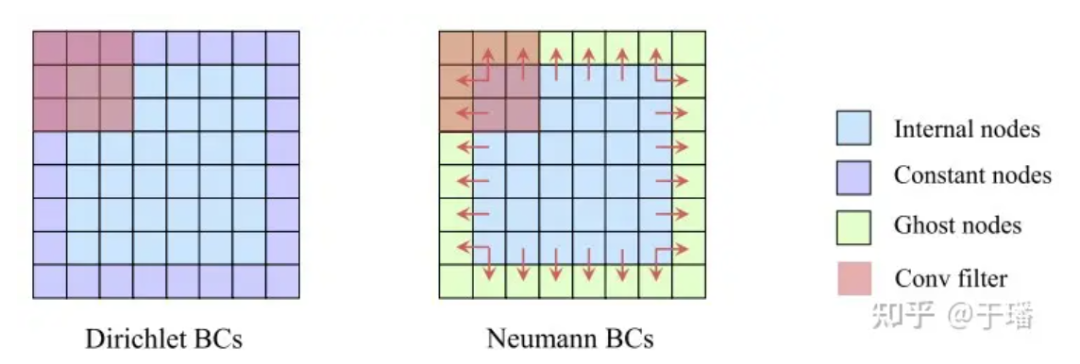Abbildung 5: Darstellung harter Einschränkungen der Randbedingungen
verlustfunktion
Da I/BC im Modell streng eingeschränkt ist, muss die Verlustfunktion nur den Restterm der PDE enthalten. Am Beispiel eines zweidimensionalen PDE-Systems kann die Verlustfunktion wie folgt ausgedrückt werden:
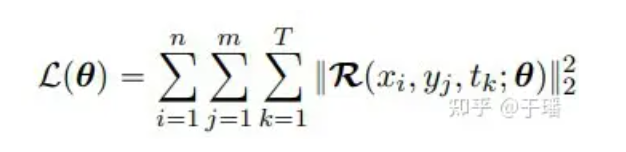
Dabei stellen n und m die Höhe und Breite des Gitters dar, T ist die Gesamtzahl der Zeitschritte und R(x, t; θ) ist das Residuum der PDE:
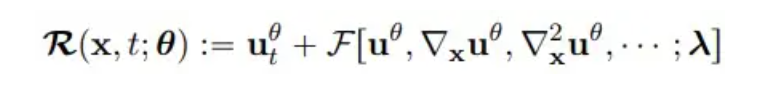
**3. ** Ergebnisanalyse
Um den Modellfehler im gesamten Bereich zu bewerten, wird der kumulative quadratische Mittelfehler (a-RMSE) zum Zeitpunkt τ wie folgt berechnet:
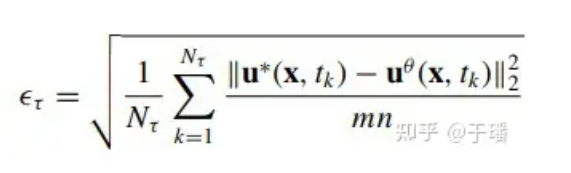
wobei Nτ die Anzahl der Zeitschritte in [0, τ] ist und u*(x, t) die Referenzlösung der Gleichung ist.
Zweidimensionale Burgers-Gleichung
Betrachten Sie ein klassisches Problem der Strömungsmechanik anhand der zweidimensionalen Burgers-Gleichung der folgenden Form:
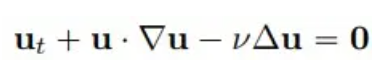
Wir wählen 4 Zeitpunkte aus: Training (t = 1,0, 2,0) und Extrapolation (t = 3,0, 4,0), um die Lösungsgenauigkeit und Extrapolationsfähigkeiten der PhyCRNet- und PINN-Methoden zu vergleichen:
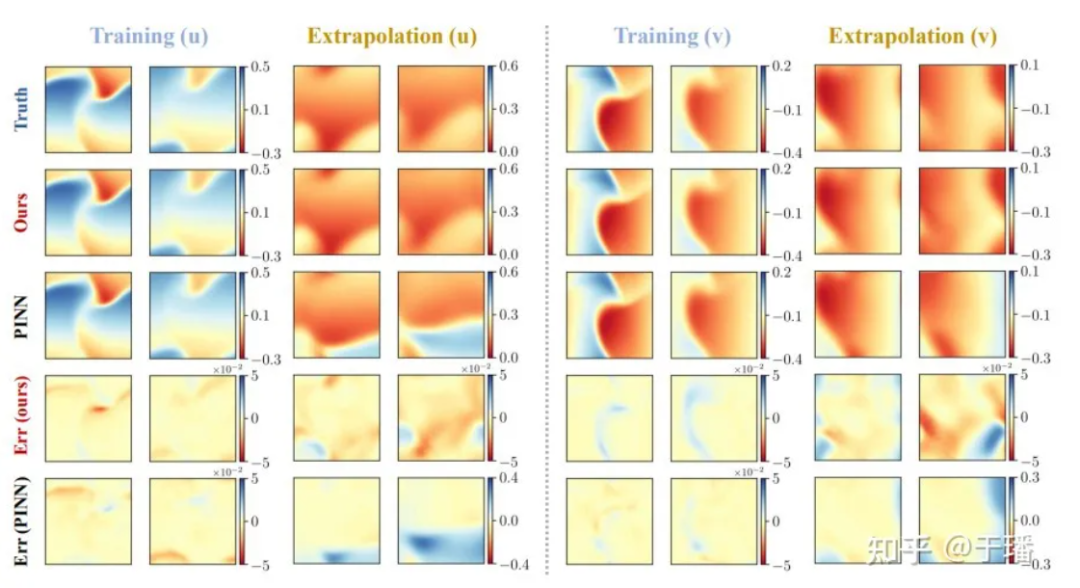Abbildung 6: Trainings- und Extrapolationsergebnisse von PhyCRNet im Vergleich zu PINNs für die zweidimensionale Burgers-Gleichung
λ-ω RD-Gleichung
Betrachten Sie als zweiten Fall ein zweidimensionales λ-ω-RD-System (oft zur Darstellung multiskaliger biochemischer Prozesse verwendet):
Unter diesen sind u und v zwei Feldvariablen, die Folgendes erfüllen:
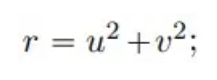
λ und ω sind zwei reellwertige Funktionen:
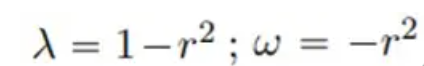
Die Referenzlösung für insgesamt 801 Zeitschritte im Bereich [-10, 10] wird durch die Spektralmethode nach Training für 200 Zeitschritte im Zeitraum [0, 5] generiert, die Referenzlösung für [5, 10]. ] Die Vorhersage erfolgt während des Zeitraums und die Vorhersageergebnisse beim Vergleich von PhyCRNet und PINN lauten wie folgt:
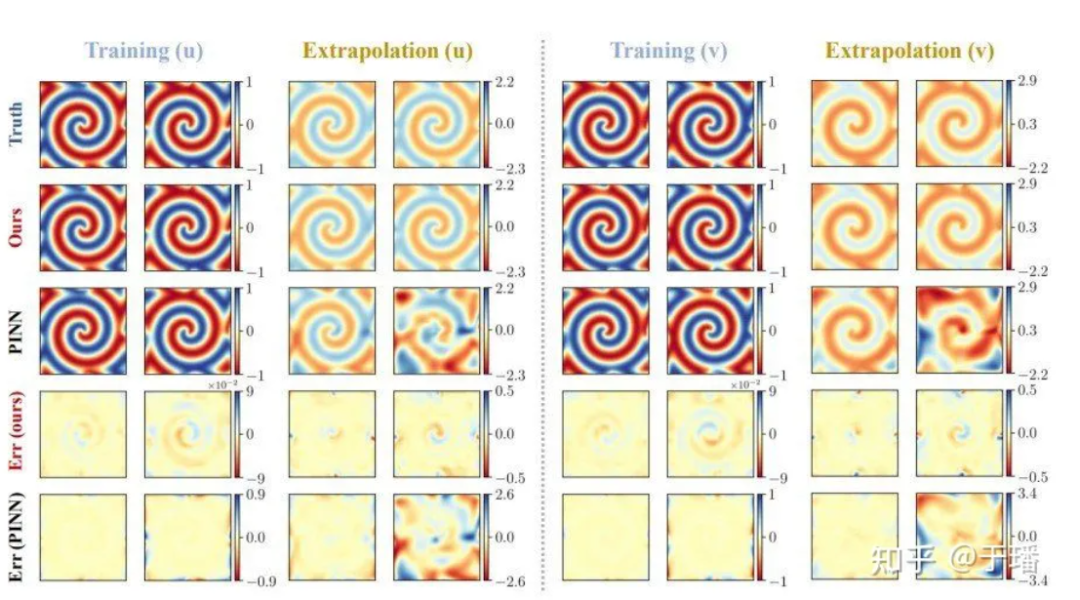Abbildung 7: Trainings- und Extrapolationsergebnisse von PhyCRNet vs. PINNs für die λ-ω RD-Gleichung
Die folgende Abbildung zeigt die Fehlerausbreitungskurven von PhyCRNet und PINNs während des Trainings und der Extrapolation in den beiden oben genannten PDE-Systemen. Es ist deutlich zu erkennen, dass PhyCRNet in beiden Phasen (insbesondere in der Extrapolationsphase) eine bessere Leistung erbringt.
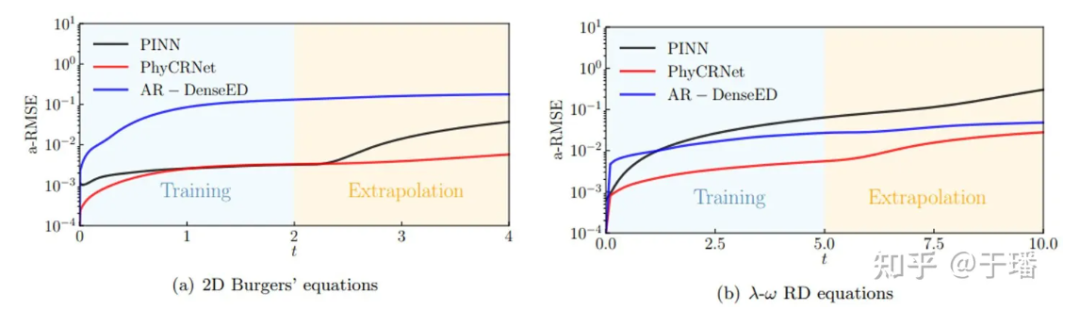Abbildung 8: Vergleich der Fehlerausbreitung von PhyCRNet und PINNs
Verweise
[1] Ren P, Rao C, Liu Y, et al. PhyCRNet: Physikinformiertes Faltungs-Rekurrent-Netzwerk zur Lösung raumzeitlicher PDEs[J]. Computermethoden in angewandter Mechanik und Ingenieurwesen, 2022, 389: 114399.
[2] https://www.sciencedirect.com/science/article/abs/pii/S0045782521006514?via%3Dihub
Ein in den 1990er Jahren geborener Programmierer hat eine Videoportierungssoftware entwickelt und in weniger als einem Jahr über 7 Millionen verdient. Das Ende war sehr bestrafend! Google bestätigte Entlassungen, die den „35-jährigen Fluch“ chinesischer Programmierer in den Flutter-, Dart- und Teams- Python mit sich brachten stark und wird von GPT-4.5 vermutet; Tongyi Qianwen Open Source 8 Modelle Arc Browser für Windows 1.0 in 3 Monaten offiziell GA Windows 10 Marktanteil erreicht 70 %, Windows 11 GitHub veröffentlicht weiterhin KI-natives Entwicklungstool GitHub Copilot Workspace JAVA ist die einzige starke Abfrage, die OLTP+OLAP verarbeiten kann. Dies ist das beste ORM. Wir treffen uns zu spät.