[Mathe] Wichtigkeitsbeispielableitung [mit Python-Implementierung]

[Mathe] Wichtigkeitsbeispielableitung [mit Python-Implementierung]

笔者在学习强化学习的过程中，经常遇到重要性采样的问题，这里简要记录一下推导过程方便以后查看。

1. Warum ist ein Wichtigkeitsbeispiel erforderlich?

Warum ist eine Wichtigkeitsstichprobe erforderlich? Angenommen, wir haben derzeit eine Zufallsvariable $X\sim X$ , und die Zufallsvariable gehorcht der Wahrscheinlichkeitsverteilung$P_{}\left(X\right)$ , unser Ziel ist es, den Erwartungswert$E_{X\sim S_{}}\left[X\right]$ , wir kennen auch die ZufallsvariableXXEine weitereleicht zugänglicheWahrscheinlichkeitsverteilungp 1 ( X ) p_1(X) für$X$$P_{}\left(X\right)$ , wie berechnen wir die Wahrscheinlichkeitsverteilung$P_{}$Erwartung EX ∼ p 0 [ X ] unter$($$X$$)$$E_{X\sim S_{}}Was\; ist\; mit\; [X]$ ? Diese Technik wird Importance Sample genannt.

2. Ableitung der diskreten Verteilung

Nehmen Sie an, dass die Zufallsvariable $X$ ist eine diskrete Wahrscheinlichkeitsverteilung und wir haben die Wahrscheinlichkeitsverteilung$P_{}Unter\; (X)$ gibt es identisch verteilte Stichproben$\{X_{}{\}}_{ich=1}^{}$. In der Wahrscheinlichkeitsverteilung $P_{}$Erwartung EX ∼ p 0 [ X ] unter$($$X$$)$$E_{X\sim S_{}}\left[X\right]$ kann durch die folgende Formel ausgedrückt werden

$$\begin{gathered} E_{X\sim S_{}}\left[X\right]=\underset{x\in X}{}{P}_{}\left(x\right)x=\underset{x\in X}{}{P}_{}\left(X\right)\underset{f\left(x\right)}{\underbrace{\frac{P_{}(x}{P_{}\left(X\right)}}}=E_{X\sim S_{}}\left[f\right(X)] \\ {E}_{X\sim S_{}}\left[X\right]=E_{X\sim S_{}}\left[f\right(X)]\approx F=\frac{}{N}\sum _{ich=1}f\left(x_{}\right)=\frac{}{N}\sum _{ich=1}\underset{\text{Wichtigkeit Gewicht}}{\underbrace{\frac{P_{}(X_{}}{P_{}\left(X_{}\right)}}}{X}_{} \end{gathered}$$

其中, $\frac{P_{}(X_{}}{P_{}\left(X_{}\right)}$wird als Wichtigkeitsgewicht bezeichnet. Mithilfe dieses Wichtigkeitsgewichts können wir die Wahrscheinlichkeitsverteilung $P_{}Stichprobe\; \{xi\; \}i$ = 1 n \ {$\{X_{}{\}}_{ich=1}^{}$, um das erwartete $E_{X\sim S_{}}\left[X\right]$ ist weg.

3. Ableitung der kontinuierlichen Verteilung

Nehmen wir in ähnlicher Weise die Zufallsvariable $X$ ist eine kontinuierliche Wahrscheinlichkeitsverteilung und wir haben die Wahrscheinlichkeitsdichtefunktion$P_{}\left(x\right)$ , es gibt identisch verteilte Stichproben$\{X_{}{\}}_{ich=1}^{}$. In der Wahrscheinlichkeitsfunktion $P_{}$Erwartung EXunter$($$x$$)\; \sim \; p\; 0\; [\; X\; ]\; \backslash mathbb\{E\}\_\{X\backslash sim\; p\_0\}[X]$$E_{X\sim S_{}}\left[X\right]$ kann durch die folgende Formel ausgedrückt werden

$$E_{X\sim S_{}}\left[X\right]={\int }_{-\infty }^{}X\times P_{}\left(x\right)dx={\int }_{-\infty }^{}{P}_{}\left(X\right)\times \underset{f\left(x\right)}{\underbrace{\frac{P_{}(x}{P_{}\left(X\right)}\times }}dx=E_{X\sim S_{}}\left[f\right(X)]$$
Anschließend verwenden wir eine große Anzahl diskreter Stichproben, um die kontinuierliche Erwartung
$$E_{X\sim S_{}}\left[X\right]=E_{X\sim S_{}}\left[f\right(X)]\approx F=\frac{}{N}\sum _{ich=1}f\left(x_{}\right)=\frac{}{N}\sum _{ich=1}\underset{\text{Wichtigkeit Gewicht}}{\underbrace{\frac{P_{}(X_{}}{P_{}\left(X_{}\right)}}}{X}_{}$$

3. Ein Beispiel

Angenommen, $X\in X=+1,-1$ , Wahrscheinlichkeitsverteilung$P_{}\left(X\right)$ erfüllt

$$P_{}(X=+1)=\mathrm{0,5},P_{}(X=-1)=\mathrm{0,5}$$

Dann ist in der Wahrscheinlichkeitsverteilung $P_{}$Die folgenden Erwartungen sind:

$$E_{X\sim S_{}}\left[X\right]=(+1)\times \mathrm{0,5}+(-1)\times \mathrm{0,5}=0$$

Angenommen, eine andere Wahrscheinlichkeitsverteilung $P_{}\left(X\right)$ erfüllt

$$P_{}(X=+1)=\mathrm{0,8},P_{}(X=-1)=\mathrm{0,2}$$

Dann ist die Wahrscheinlichkeitsverteilung $P_{}$Die folgenden Erwartungen sind:

$$E_{X\sim S_{}}\left[X\right]=(+1)\times \mathrm{0,8}+(-1)\times \mathrm{0,2}=\mathrm{0,6}$$

Durch Wichtigkeitsstichprobe können wir die Wahrscheinlichkeitsverteilung $P_{}\left(X\right)$ zur Berechnung der Wahrscheinlichkeitsverteilung$P_{}$Der erwartete Wert unter$($$X$$)\; ist$

$$E_{X\sim S_{}}\left[X\right]=\frac{}{N}\sum _{ich=1}\frac{P_{}(X_{}}{P_{}\left(X_{}\right)}{X}_{}$$

Der Implementierungscode lautet wie folgt:

import numpy as np
import matplotlib.pyplot as plt
# reproducible
np.random.seed(0)

# 定义元素和对应的概率
elements = [1, -1]
probs1 = [0.5, 0.5]
probs2 = [0.8, 0.2]

# 重要性采样 importance sample
sample_times = 300
sample_list = []
i_sample_list = []
average_list = []
importance_list = []
for i in range(sample_times):
    sample = np.random.choice(elements, p=probs2)
    sample_list.append(sample)
    average_list.append(np.mean(sample_list))
    if sample == elements[0]:
        i_sample_list.append(probs1[0] / probs2[0] * sample)
    elif sample == elements[1]:
        i_sample_list.append(probs1[1] / probs2[1] * sample)
    importance_list.append(np.mean(i_sample_list))



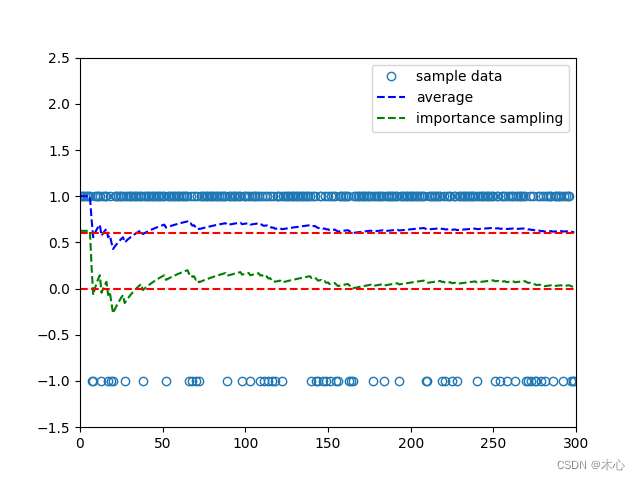
plt.plot(range(len(sample_list)), sample_list, 'o', markerfacecolor='none', label='sample data')
plt.plot(range(len(average_list)), average_list, 'b--', label='average')
plt.plot(range(len(importance_list)), importance_list, 'g--', label='importance sampling')
plt.axhline(y=0.6, color='r', linestyle='--')
plt.axhline(y=0, color='r', linestyle='--')
plt.ylim(-1.5, 2.5) # 限制y轴显示范围
plt.xlim(0,sample_times) # 限制x轴显示范围
plt.legend(loc='upper right')
plt.show()

Die Ergebnisse sind wie folgt. Es ist ersichtlich, dass unter Verwendung von $P_{}(\_\_$ _$E_{X\sim S_{}}[\_\_$ _$E_{X\sim S_{}}\left[X\right]=0$。