Isotropie ist eine sehr wichtige und grundlegende Eigenschaft in hochdimensionalen Zufallsvektoren. Die chinesische Übersetzung heißt Isotropie, ähm ... Es ist wirklich schwierig, ihre Bedeutung allein anhand des Namens zu verstehen ... (Aber sie ist besser als die Robust-Übersetzung viel besser)
Der Kern der Isotropie in der Wahrscheinlichkeitstheorie ist die „Einheitsvarianz“, und es ist für uns sehr einfach, eine Zufallsvariable mit einem Mittelwert von 0 und einer Varianz von 1 zu untersuchen. Bei hochdimensionalen Zufallsvektoren wird die Varianzbeschränkung zur Kovarianzbeschränkung. Der isotrope Zufallsvektor bezieht sich auf einen Zufallsvektor mit einer Varianz von 1 in jede Richtung und einer Kovarianz von 0 in verschiedenen Richtungen. Die mathematische Darstellung ist wie folgt:
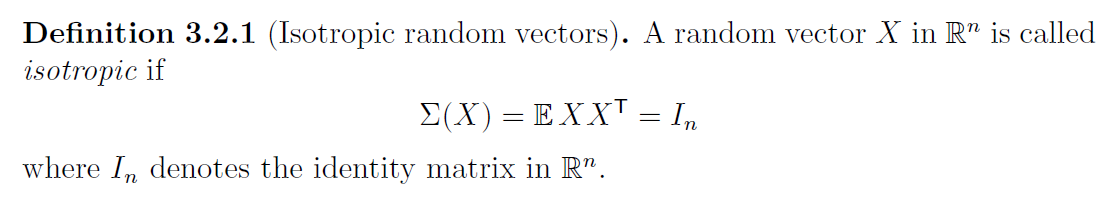
Neben der Definition gibt es noch andere Möglichkeiten, die Isotropie zu bestimmen. Denn eine Zufallsvariable ist genau dann isotrop, wenn
Das heißt, das innere Produkt eines isotropen Zufallsvektors mit einem beliebigen Vektor ist gleich dem dieses Vektors

Verteilungsvergleichstabelle: Die linke Seite ist eine isotrope Verteilung, die rechte ist keine isotrope Verteilung
Das obige Bild zeigt den Vergleich zwischen isotroper Verteilung und nichtisotroper Verteilung. Es ist deutlich zu erkennen, dass die isotrope Verteilung gleichmäßig in verschiedene Richtungen verteilt ist, was eine intuitive Erklärung von „Isotropie“ sein sollte.