一、前言
旅行商问题(Traveling Salesman Problem,TSP)一直是运筹学与计算智能领域的经典难题:给定若干城市,要求在访问每个城市恰好一次的前提下规划一条最短(或代价最低)的巡回路线。由于TSP具备组合爆炸特性,当城市数量增多时,问题规模呈指数增长,故而在精确算法难以短时间内求解的情况下,群体智能算法与元启发式算法应运而生。粒子群优化(Particle Swarm Optimization,PSO)是一种基于群体协同和个体最优记忆的随机搜索技术,最初应用于连续空间优化,而后逐步衍生出适应离散优化(如TSP)的问题变体。
二、技术与原理简介
1. 旅行商问题(TSP)概述
旅行商问题可描述为:在一张含有 n 个城市节点的加权完全图上,寻找一条最短回路,使得该回路经过每个城市一次且仅一次并最终回到起点。形式化定义如下:
- 给定城市集合 V={1,2,…,n};
- 城市间距离(或代价)矩阵 D=[dij],其中 dij 表示从城市 i 到城市 j 的距离,且 dij=dji(对称TSP);
- 目标:寻找一个排列 π(即访问顺序),使得以下目标函数最小化:
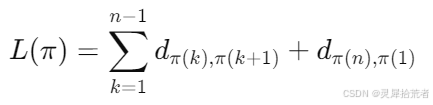
其中,π(k) 表示第 k 个访问的城市索引。
TSP 是 NP-hard 问题,城市数稍大时,若使用穷举或动态规划则计算量极其庞大,因此实际应用中多采用近似算法或启发式/元启发式算法(如遗传算法GA、蚁群算法ACO、粒子群算法PSO等)。
2. 粒子群优化(PSO)简介
PSO 最初由 Eberhart 与 Kennedy 在 1995 年提出,灵感来自鸟群或鱼群的协同搜索行为。它通过一群“粒子”在解空间中迭代更新位置和速度,逐渐逼近最优解。
在经典连续PSO中,每个粒子 iii 拥有位置向量 xi 和速度向量 vi,并存储个体历史最优位置 pi 以及全局历史最优位置 g。更新方程通常写作:

其中:w 为惯性权重;c1,c2 为加速度常数;r1,r2 为 [0,1] 之间的随机数。
3. TSP-PSO 的离散化与关键挑战
TSP 的解是一个城市访问序列,而不是连续向量,因此需要对PSO做以下改造或启发式操作:
-
位置表示
- 将“位置”定义为一个长度为 n 的城市序列(Permutation),粒子之间交换或交叉片段可视为位置更新;
- 或将“位置”视为排列映射,如 xi = [城市1, 城市2, ..., 城市n]。
-
速度与更新
- 速度难以在离散序列上直接定义,故往往通过交叉(Crossover)、变异(Mutation)等算子来替代PSO中的速度概念;
- 有些文献中采用“交换序列”或“邻域变换”来模拟PSO速度。
-
个体最优 pi 与全局最优 g
- 对应各自历史上取得最小路径长度的城市顺序;
- 在更新时,部分片段或基因来自 pi 与 g,以实现“粒子”向更优解收敛。
总之,TSP-PSO大多呈现出“半PSO、半GA”的混合风格:利用PSO的全局记忆机制与GA的交叉/变异运算,令粒子在离散的排列空间中迭代演化。
三、代码详解
本文的 MATLAB 代码主要分为以下几个部分:
1. 数据加载与可视化
data=load('eil51.txt');
cityCoor=[data(:,2) data(:,3)];%城市坐标矩阵
figure
plot(cityCoor(:,1),cityCoor(:,2),'ms','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','g')
legend('城市位置')
ylim([4 78])
title('城市分布图','fontsize',12)
xlabel('km','fontsize',12)
ylabel('km','fontsize',12)
grid on
说明:
load('eil51.txt'):载入城市数据文件,这里eil51.txt常见于TSP实例数据,含有51个城市的坐标;cityCoor提取第二、三列作为坐标(第一列常为城市编号);- 通过
plot命令绘制城市分布图,并加上图例、坐标轴说明、网格等修饰。 ylim([4 78])是对y轴范围做适当限制。- 该步骤可帮助读者直观了解城市在平面坐标系的散点分布,为后续算法验证打下基础。
2. 计算城市间距离矩阵
n=size(cityCoor,1); %城市数目
cityDist=zeros(n,n); %城市距离矩阵
for i=1:n
for j=1:n
if i~=j
cityDist(i,j)=((cityCoor(i,1)-cityCoor(j,1))^2+...
(cityCoor(i,2)-cityCoor(j,2))^2)^0.5;
end
cityDist(j,i)=cityDist(i,j);
end
end
说明:
n=size(cityCoor,1)获取城市数目;cityDist初始化 n×n 矩阵,用于存储两两城市的欧几里得距离;- 双重
for循环计算distance = sqrt((x_i - x_j)^2 + (y_i - y_j)^2); - 代码中将
cityDist(j,i)=cityDist(i,j)做对称赋值,说明该 TSP 是对称的。
3. 种群初始化
nMax=200; %进化次数
indiNumber=1000; %个体数目
individual=zeros(indiNumber,n);
%初始化粒子位置
for i=1:indiNumber
individual(i,:)=randperm(n);
end
说明:
nMax=200表示最大迭代轮数;indiNumber=1000指定粒子(或个体)数目为1000,较大规模有助于增强多样性;individual用于存放每个粒子的路径序列,每行一个路径。randperm(n)产生长度为 n 的随机排列,保证不重复访问城市。
4. 计算适应度并初始化
indiFit=fitness(individual,cityCoor,cityDist);
[value,index]=min(indiFit);
tourPbest=individual; %当前个体最优
tourGbest=individual(index,:) ; %当前全局最优
recordPbest=inf*ones(1,indiNumber); %个体最优记录
recordGbest=indiFit(index); %群体最优记录
xnew1=individual;
说明:
indiFit=fitness(...):调用自定义函数fitness计算每个个体的路径长度;[value,index]=min(indiFit)找到适应度最低(路径最短)者,作为全局最优;tourPbest=individual;将初始个体自身当作“个体最优”,tourGbest为全局最优;recordPbest记录每个个体迄今最好的适应度值;recordGbest记录全局最优适应度。xnew1=individual;用于暂存交叉、变异后的新解。
5. 主循环
L_best=zeros(1,nMax);
for N=1:nMax
N
%计算适应度值
indiFit=fitness(individual,cityCoor,cityDist);
%更新当前最优和历史最优
for i=1:indiNumber
if indiFit(i)<recordPbest(i)
recordPbest(i)=indiFit(i);
tourPbest(i,:)=individual(i,:);
end
if indiFit(i)<recordGbest
recordGbest=indiFit(i);
tourGbest=individual(i,:);
end
end
[value,index]=min(recordPbest);
recordGbest(N)=recordPbest(index);
%% 交叉操作
for i=1:indiNumber
% 与个体最优进行交叉
...
% 与全体最优进行交叉
...
%% 变异操作
...
end
[value,index]=min(indiFit);
L_best(N)=indiFit(index);
tourGbest=individual(index,:);
end
说明:
L_best(N)=...:记录第 N 次迭代后的群体最佳适应度;- 交叉操作:分两步进行,先与个体最优交叉,再与全局最优交叉;
- 通过
c1, c2随机产生交叉位; - 将对应片段插入当前解并去除重复城市;
- 若新路径距离更短则更新;
- 通过
- 变异操作:随机选两个位置交换,若改进则保留;
- 通过这三个步骤(与pbest交叉、与gbest交叉、变异),相当于离散PSO中位置更新+速度概念的混合操作;
- 更新完后再次寻找当代最优并存储到
L_best(N)。
6. 结果作图
figure
plot(L_best)
title('算法训练过程')
xlabel('迭代次数')
ylabel('适应度值')
grid on
figure
hold on
plot([cityCoor(tourGbest(1),1),cityCoor(tourGbest(n),1)],...
[cityCoor(tourGbest(1),2),cityCoor(tourGbest(n),2)],...
'ms-','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','g')
...
scatter(cityCoor(:,1),cityCoor(:,2));
title('规划路径','fontsize',10)
xlabel('km','fontsize',10)
ylabel('km','fontsize',10)
grid on
ylim([4 80])
说明:
- 第一幅图:
plot(L_best)显示迭代过程中最佳适应度(最短路径)的变化,若曲线逐渐收敛说明算法在改进; - 第二幅图:绘制最终最优路径
tourGbest;- 先连最后一个城市与第一个城市,再连相邻城市;
- 用散点或标记展示各城市位置,直观呈现路线走向。
7. 完整代码
%% 该文件演示基于TSP-PSO算法
clc;clear
%% 下载数据
data=load('eil51.txt');
cityCoor=[data(:,2) data(:,3)];%城市坐标矩阵
figure
plot(cityCoor(:,1),cityCoor(:,2),'ms','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','g')
legend('城市位置')
ylim([4 78])
title('城市分布图','fontsize',12)
xlabel('km','fontsize',12)
ylabel('km','fontsize',12)
%ylim([min(cityCoor(:,2))-1 max(cityCoor(:,2))+1])
grid on
%% 计算城市间距离
n=size(cityCoor,1); %城市数目
cityDist=zeros(n,n); %城市距离矩阵
for i=1:n
for j=1:n
if i~=j
cityDist(i,j)=((cityCoor(i,1)-cityCoor(j,1))^2+...
(cityCoor(i,2)-cityCoor(j,2))^2)^0.5;
end
cityDist(j,i)=cityDist(i,j);
end
end
nMax=200; %进化次数
indiNumber=1000; %个体数目
individual=zeros(indiNumber,n);
%^初始化粒子位置
for i=1:indiNumber
individual(i,:)=randperm(n);
end
%% 计算种群适应度
indiFit=fitness(individual,cityCoor,cityDist);
[value,index]=min(indiFit);
tourPbest=individual; %当前个体最优
tourGbest=individual(index,:) ; %当前全局最优
recordPbest=inf*ones(1,indiNumber); %个体最优记录
recordGbest=indiFit(index); %群体最优记录
xnew1=individual;
%% 循环寻找最优路径
L_best=zeros(1,nMax);
for N=1:nMax
N
%计算适应度值
indiFit=fitness(individual,cityCoor,cityDist);
%更新当前最优和历史最优
for i=1:indiNumber
if indiFit(i)<recordPbest(i)
recordPbest(i)=indiFit(i);
tourPbest(i,:)=individual(i,:);
end
if indiFit(i)<recordGbest
recordGbest=indiFit(i);
tourGbest=individual(i,:);
end
end
[value,index]=min(recordPbest);
recordGbest(N)=recordPbest(index);
%% 交叉操作
for i=1:indiNumber
% 与个体最优进行交叉
c1=unidrnd(n-1); %产生交叉位
c2=unidrnd(n-1); %产生交叉位
while c1==c2
c1=round(rand*(n-2))+1;
c2=round(rand*(n-2))+1;
end
chb1=min(c1,c2);
chb2=max(c1,c2);
cros=tourPbest(i,chb1:chb2);
ncros=size(cros,2);
%删除与交叉区域相同元素
for j=1:ncros
for k=1:n
if xnew1(i,k)==cros(j)
xnew1(i,k)=0;
for t=1:n-k
temp=xnew1(i,k+t-1);
xnew1(i,k+t-1)=xnew1(i,k+t);
xnew1(i,k+t)=temp;
end
end
end
end
%插入交叉区域
xnew1(i,n-ncros+1:n)=cros;
%新路径长度变短则接受
dist=0;
for j=1:n-1
dist=dist+cityDist(xnew1(i,j),xnew1(i,j+1));
end
dist=dist+cityDist(xnew1(i,1),xnew1(i,n));
if indiFit(i)>dist
individual(i,:)=xnew1(i,:);
end
% 与全体最优进行交叉
c1=round(rand*(n-2))+1; %产生交叉位
c2=round(rand*(n-2))+1; %产生交叉位
while c1==c2
c1=round(rand*(n-2))+1;
c2=round(rand*(n-2))+1;
end
chb1=min(c1,c2);
chb2=max(c1,c2);
cros=tourGbest(chb1:chb2);
ncros=size(cros,2);
%删除与交叉区域相同元素
for j=1:ncros
for k=1:n
if xnew1(i,k)==cros(j)
xnew1(i,k)=0;
for t=1:n-k
temp=xnew1(i,k+t-1);
xnew1(i,k+t-1)=xnew1(i,k+t);
xnew1(i,k+t)=temp;
end
end
end
end
%插入交叉区域
xnew1(i,n-ncros+1:n)=cros;
%新路径长度变短则接受
dist=0;
for j=1:n-1
dist=dist+cityDist(xnew1(i,j),xnew1(i,j+1));
end
dist=dist+cityDist(xnew1(i,1),xnew1(i,n));
if indiFit(i)>dist
individual(i,:)=xnew1(i,:);
end
%% 变异操作
c1=round(rand*(n-1))+1; %产生变异位
c2=round(rand*(n-1))+1; %产生变异位
while c1==c2
c1=round(rand*(n-2))+1;
c2=round(rand*(n-2))+1;
end
temp=xnew1(i,c1);
xnew1(i,c1)=xnew1(i,c2);
xnew1(i,c2)=temp;
%新路径长度变短则接受
dist=0;
for j=1:n-1
dist=dist+cityDist(xnew1(i,j),xnew1(i,j+1));
end
dist=dist+cityDist(xnew1(i,1),xnew1(i,n));
if indiFit(i)>dist
individual(i,:)=xnew1(i,:);
end
end
[value,index]=min(indiFit);
L_best(N)=indiFit(index);
tourGbest=individual(index,:);
end
%% 结果作图
figure
plot(L_best)
title('算法训练过程')
xlabel('迭代次数')
ylabel('适应度值')
grid on
figure
hold on
plot([cityCoor(tourGbest(1),1),cityCoor(tourGbest(n),1)],[cityCoor(tourGbest(1),2),...
cityCoor(tourGbest(n),2)],'ms-','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','g')
hold on
for i=2:n
plot([cityCoor(tourGbest(i-1),1),cityCoor(tourGbest(i),1)],[cityCoor(tourGbest(i-1),2),...
cityCoor(tourGbest(i),2)],'ms-','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','g')
hold on
end
legend('规划路径')
scatter(cityCoor(:,1),cityCoor(:,2));
title('规划路径','fontsize',10)
xlabel('km','fontsize',10)
ylabel('km','fontsize',10)
grid on
ylim([4 80])
8. 子代码 dist.m
function dist=dist(x,D)
n=size(x,2);
dist=0;
for i=1:n-1
dist=dist+D(x(i),x(i+1));
end
dist=dist+D(x(1),x(n));
9. 子代码 fitness.m
function indiFit=fitness(x,cityCoor,cityDist)
%% 该函数用于计算个体适应度值
%x input 个体
%cityCoor input 城市坐标
%cityDist input 城市距离
%indiFit output 个体适应度值
m=size(x,1);
n=size(cityCoor,1);
indiFit=zeros(m,1);
for i=1:m
for j=1:n-1
indiFit(i)=indiFit(i)+cityDist(x(i,j),x(i,j+1));
end
indiFit(i)=indiFit(i)+cityDist(x(i,1),x(i,n));
end 


四、总结与思考
-
算法收敛与性能
- 该TSP-PSO思路通过“个体最优 + 全局最优 + 交叉 + 变异”的方式替代传统PSO的速度更新,将PSO的记忆与协同特性移植到TSP排列空间;
- 实践表明,对于中小规模的TSP(如 50~200 个城市),此方法可较快收敛到较优解,且实现相对简洁。
-
局限性
- 对大规模TSP(上千城市)仍有收敛速度与解质量的挑战,需要并行化或更复杂的交叉/变异策略;
- 算法参数如
indiNumber=1000、nMax=200在不同TSP实例下需做调参; - 交叉与变异对离散PSO的贡献较大,但也可能造成一定的随机扰动,需要在保持种群多样性与加速收敛间平衡。
-
可拓展方向
- 混合算法:可与遗传算法(GA)或禁忌搜索(Tabu Search)结合,进一步提升精度;
- 自适应策略:在迭代过程中自动调节交叉率、变异率,或引入动态惯性权重;
- 并行与GPU加速:对大规模TSP,可将适应度计算和群体操作并行化;
- 多目标扩展:若考虑耗时、费用、车辆载重等多维度约束,可将TSP-PSO推广到车辆路径问题(VRP)等更复杂场景。
-
实际应用
- TSP-PSO在物流、旅行规划、印刷电路板钻孔、机器人巡检等场合均有潜在应用价值;
- 若结合地理信息系统(GIS)或云计算平台,可为城市级别路径规划提供启发式求解。
【作者声明】
本文内容基于作者对 PSO-TSP实现过程的实验与总结,所有数据和代码均为原创。文章中的观点仅代表个人见解,供读者参考交流。若有任何问题或建议,欢迎在评论区留言讨论,共同促进技术进步。
【关注我们】
如果您对神经网络、群智能算法及人工智能技术感兴趣,请关注我们,获取更多前沿技术文章、实战案例及技术分享!欢迎点赞、收藏并转发,与更多朋友一起探讨与交流!