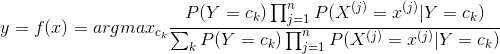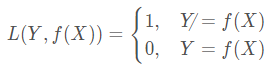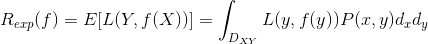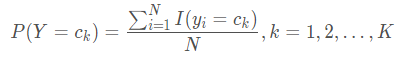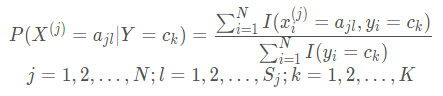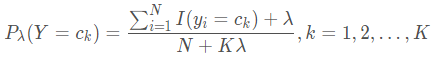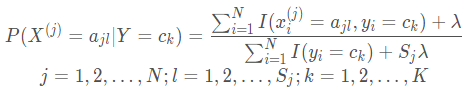【朴素贝叶斯】 Part1——朴素贝叶斯基本原理

1. 概率论基本知识回顾

• （1）条件概率：设A，B是两个事件，且P(A)>0，称 $P(B|A) = \frac {P(AB)}{P(A)}$ 为在事件A发生的条件下事件B发生的概率。

• （2）乘法定理：设P(A)>0，称 $P(AB) = {P(B|A)}{P(A)}$ 为事件A，B同时发生的概率等于事件A发生的概率与事件A发生的条件下事件B发生的概率的乘积。

• （3）全概率公式：设B1，B2，…，Bn是样本空间S的一个全划分，则：
  $P(A)=P(A\cap S) \\ =P(A\cap(B1\cup B2\cup ...\cup Bn)) \\ =P(A\cap B1)+P(A\cap B2)+...+P(A\cap Bn) \\ =P(A|B1)P(B1)+P(A|B2)P(B2)+...+P(A|Bn)P(Bn)$

• （4）贝叶斯定理：根据条件概率的定义，事件 A 发生的条件下事件 B 发生的概率、事件 B 发生的条件下事件 A 发生的概率分别为：
  $P(B|A) = \frac {P(AB)}{P(A)}$

  $P(A|B) = \frac {P(AB)}{P(B)}$

  结合这两个方程式，我们可以得到：
  ${P(B|A)}{P(A)} = P(AB) = {P(A|B)}{P(B)}$

  上式两边同除以 P(B)，若P(B)>0，我们可以得到贝叶斯定理：
  $P(A|B) = \frac {{P(B|A)}{P(A)}}{P(B)}$

P(A)是 A 的先验概率，之所以称为“先验”是因为它不考虑任何 B 方面的因素。
P(A|B)是已知 B 发生后 A 的条件概率，也由于得自 B 的取值而被称作 A 的后验概率。
P(B|A)是已知 A 发生后 B 的条件概率，也由于得自 A 的取值而被称作 B 的后验概率。
P(B)是 B 的先验概率，也作标淮化常量（normalizing constant）。
贝叶斯定理可表述为：
后验概率 = (相似度 * 先验概率)/标淮化常量

2. 朴素贝叶斯法的学习与分类原理

2.1 基本方法

• 输入： 训练数据集 $T= \{(x_{1},y_{1}),(x_{2},y_{2}),...,(x_{N},y_{N})\}$
  T由X和Y的联合概率分布P(X,Y)独立同分布产生
  其中数据集特征向量 $x_{i}=(x_{i}^{(1)},x_{i}^{(2)},...,x_{i}^{(n)})^{T}$

• 输出： 类标记 $y = \{c_{1},c_{2},...,c_{k}\}$

• 朴素贝叶斯法通过训练数据集学习联合概率分布P(X,Y)：

  • 先验概率分布： $P(Y=c_{k})$ , k=1,2,…,K
  • 条件概率分布：
    • $P(X=x | Y=c_{k}) \\= P(X^{(1)}=x^{(1)},X^{(2)}=x^{(2)},...,X^{(n)}=x^{(n)} | Y=c_{k})$

• 朴素贝叶斯法假设各个特征之间相互独立，即用于分类的特征在类确定的条件下都是相互独立的，具体条件独立性假设：

  • $P(X=x | Y=c_{k}) \\ = P(X^{(1)}=x^{(1)},X^{(2)}=x^{(2)},...,X^{(n)}=x^{(n)} | Y=c_{k}) \\ = \prod_{j=1}^{n}P(X^{(j)}=x^{(j)}|Y=c_{k})$

• 朴素贝叶斯法分类时，对于给定输入的特征x，根据贝叶斯定理计算后验概率 $P(Y=c_{k}|X=x)$：
  

• 朴素贝叶斯分类器：
  
  即：最终贝叶斯分类器可表示为：

  $y=argmax_{c_{k}}P(Y=c_{k})\prod_{j=1}^{n}P(X^{(j)}=x^{(j)}|Y=c_{k})$

2.2 后验概率最大化含义

• 朴素贝叶斯法将实例分到后验概率最大的类中，如何得到最好的分类结果，只有损失函数值越小模型效果越好，等价于期望风险最小化，假设选取0-1损失函数：
  

• 定义损失函数 $L(Y,f(X))$ 的数学期望作为期望风险函数为 $R_{exp}(f)$：
  
  由上述期望风险函数，进行如下推导：
  
  这里设： $H(X)=\int_{D_{Y}}L(y,f(y))P(y|x)d_{y}$

  那么期望风险函数可表示为：

  $R_{exp}(f)=E[L(Y,f(X))]=\int_{D_{X}}H(X)*P(x)d_{x}$

  我们发现上述推导得到的积分函数中，H(x)中的各项及P(x)都大于0，所以积分过程中不存在积分域内的两块积分相减的情况，因此，求期望风险最小化，就等价于求H(x)P(x)的最小值。对于任意的一个x，P(X=x)为常数，那么最小值一定是在H(x)取最小值的时候取到。因此对期望风险函数的求解可以转为所谓的求条件期望的最小值：

  $H(X)=\int_{D_{Y}}L(y,f(y))P(y|x)d_{y}$

  而对于离散型随机变量，H(X) 可以转化为：

  $H(X)=\sum_{k=1}^{K}[L(c_{k},f(X))]P(c_{k}|X)$

• 取条件期望：

  $R_{exp}(f)=E_{X}\sum_{k=1}^{K}[L(c_{k},f(X))]P(c_{k}|X)$

• 为了使期望风险最小化，只需要求条件期望的最小值，只需对X=x逐个极小化，由此得到：
  
  这样一来，根据期望风险最小化准则就得到了后验概率最大化准则：

  $f(x)=argmax_{c_{k}}P(c_{k}|X=x)$

3. 朴素贝叶斯法的参数估计

• 朴素贝叶斯法中，学习就是估计 $P(Y=c_{k})$和 $P(X^{(j)}=x^{(j)}|Y=c_{k})$值

3.1 极大似然估计

• 先验概率 $P(Y=c_{k})$的极大似然估计是：
  
• 条件概率 $P(X^{(j)}=a_{jl}|Y=c_{k})$的极大似然估计是：
  
  其中 $x_{i}^{(j)}$ 表示第 i 个样本的第 j 个特征 $x_{i}^{(j)}\epsilon \left \{ a_{j1},a_{j2},...,a_{js_{j}} \right \}$
  $a_{jl}$表示第 j 个特征可能取的第 l 个值

3.2 贝叶斯估计

• 先验概率 $P(Y=c_{k})$的贝叶斯估计是：
  
• 条件概率 $P(X^{(j)}=a_{jl}|Y=c_{k})$的贝叶斯估计是：
  
  上式中的 $\lambda\geq0$，等价于在随机变量各个取值的频数上赋予一个正数 $\lambda$，这样就弥补了极大似然估计可能会出现所要估计的概率值为0的缺陷。当 $\lambda=0$时，就是极大似然估计；当 $\lambda=1$时，就称拉普拉斯平滑。
• 有关极大似然估计法、贝叶斯估计法推导证明朴素贝叶斯法中的概率公式请参照以下博客：
  证明朴素贝叶斯法中的概率估计公式
• 到此，朴素贝叶斯基本原理介绍完毕，如有错误欢迎指正，下节将将介绍python如何实现朴素贝叶斯分类算法及应用实例。
• 参考资料：李航《统计学习方法》