泛函及变分简介

在科学技术上，常常需要确定某一个函数 z = f(x) 的极大值或者极小值；这种计算分析是微积分里大家所熟知的。但是，我们经常还要去确定一类特殊的量即泛函的极大值或者极小值。这就是变分法所处理的范围。

1. 历史上有名的变分问题

A，B两点不在一条垂线上，找到A,B两点之间的一条曲线，使得物体自A点滑到B点（无摩擦力）的时间最短。

设A点与原点重合，B点坐标为(x1, y1), 当物体滑到点P(x,y)时，其速度为v，物体重量为m。由能量守恒定律我们有：

以s为曲线从A点算起的弧长，则

又有

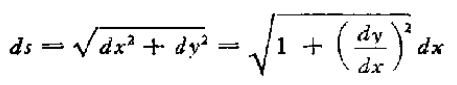
所以

两边积分可以得到

这里，T是y(x)某种广义的函数，人们称这一类型的广义函数为泛函。变量的值是由一个或者多个函数的选取而确定的，这个变量称为这些函数的泛函。上面提到的最速下降问题，可以说成：在满足 y(0)，y(x1) = y1的一切y(x)中，选取一个，使得泛函T(上式)为最小值。

2. 变分及其特性

我们知道，我们可以通过求导数等方法求得函数的极大极小值，那么对于泛函怎样求极值呢？让我们把泛函相关的特性与函数做相应的对比以便研究。

（1）泛函定义

由此可知，函数是变量与变量的关系，而泛函是函数与变量的关系，泛函是广义的函数。

（2）微分和变分

泛函 $\Pi[y(x)]$ 的宗量y(x)的增量在它很小的时候称为变分，用 $\delta y(x)$ 来标志，其指y和跟它相接近的y1(x)之差，即 $\delta y(x) = y(x) - y_{1}(x)$ ；那么，y(x)和y1(x)要怎么样才算很接近？一个简单的理解是，在一切x上，y和y1的差都很小，更近一步，如果y和y1k阶导数也是相近的，我们称之为k阶接近的。

（3）泛函的连续

先复习下函数的连续：

函数连续是基于x方向上改变的，而泛函的连续是基于宗量y(x)上的改变：

（4）函数的微分和泛函的变分

1. 函数微分定义一

先来看函数微分，我们知道函数的增量可以展开为线性项和非线性项

A(x)和delta-x无关，和delta-x有关，并且，这时，我们称y(x)是可微的，其线性部分A(x)称为函数的微分

这里A(x)为y的导数是因为根据导数的定义：。以上可以看到，函数的微分是函数增量的主部，这个主部对于 delta-x来说是线性的。

2. 函数微分定义二

函数微分可以有另外一种定义，设 $\varepsilon$ 为一个小参数，并将对 $\varepsilon$ 求导，即可以得到：，当 $\varepsilon$ 趋近于0的时候，这证明了y在 $\varepsilon$ 处的导数就等于y在x处的积分。

3. 泛函变分定义一

泛函的变分也有类似的定义，泛函的增量为，其可展开为线性泛函项和非线性的泛函项：，线性泛函项，即有下列性质：

这里L就是泛函的变分，用 $\delta \Pi$ 表示。泛函的变分是泛函增量的主部，这个主部对于变分 $\delta y(x)$ 来说是线性的。

4.泛函微分定义二

3 欧拉公式

在推导欧拉公式之前，首先介绍下变分法的基本预备定理：

证明暂且不论，这不是重点。前面2节介绍了泛函和变分相关知识，但是泛函的极值到底是如何求得的呢？？本节我们把精力集中在从泛函变分求取欧拉方程上面。

首先求泛函的变分

由含参定积分求导公式我们可以得到

令 $\varepsilon$ 趋近于0，得到

根据分部分积分法则

$\int_{x_{1}}^{x_{2}} \frac{\partial F}{\partial y{}'}\delta y{}'dx = \frac{\partial F}{\partial y{}'}\delta y|_{x_{1}}^{x_{2}} - \int_{x_{1}}^{x_{2}}\delta y\frac{d(\frac{\partial F}{\partial y{}'})}{dx} dx$