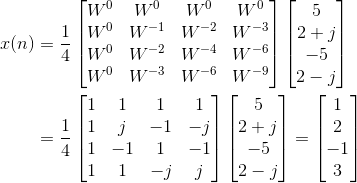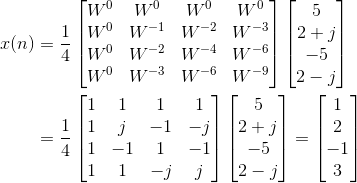离散傅里叶变换 --- DFT

本文转载自https://blog.csdn.net/shenziheng1/article/details/52862606/

1. 闲话

什么是频域？从我们出生，我们看到的世界都以时间贯穿，股票的走势、人的身高、汽车的轨迹都会随着时间发生改变。这种以时间作为参照来观察动态世界的方法我们称其为时域分析。而我们也想当然的认为，世间万物都在随着时间不停的改变，并且永远不会静止下来。但如果我告诉你，用另一种方法来观察世界的话，你会发现世界是永恒不变的，你会不会觉得我疯了？我没有疯，这个静止的世界就叫做频域。

在时域，我们观察到钢琴的琴弦一会上一会下的摆动，就如同一支股票的走势；而在频域，只有那一个永恒的音符。所以我们眼中看似落叶纷飞变化无常的世界，实际只是躺在上帝怀中一份早已谱好的乐章。

2. 数学推导

我们知道，在离散傅里叶级数（DFS）中，离散时间周期序列在时域是离散的 $n$ ，其频谱是离散频率周期序列，在频域也是离散的 $k$，理论上解决了时域离散和频域离散的对应关系问题。但由于其在时域和频域都是周期序列，所以都是无限长序列。无限长序列在计算机运算仍然是无法实现。为此必须取有限长序列来建立其时域离散和频域离散的对应关系。

DFS的主值序列：

我们知道，离散时间周期序列是一个无限长序列，其傅立叶级数展开式为：
$\tilde x(n) = IDFS[\tilde X(k)] = \frac{1}{N} \sum_{k=0}^{N-1}\tilde X(k) e^{j\frac{2\pi}{N}kn}, (-\infin<n<+\infin)$

可以看出时间点序列 $n$是以 $N$为周期的，如果只取其一个周期，称之为 $\tilde x(n)$的主值序列：
$x(n) = \tilde x(n) | (0 \leq n \leq N-1)$

主值序列 $x(n)$就是一个长度为 $N$的有限长离散时间序列。同理， $DFS$也是一个无限长序列，即傅里叶系数：

$\tilde x(k) = DFS[\tilde x(n)] = \sum_{n=0}^{N-1}\tilde x(n)e^{-j\frac{2\pi}{N}kn}, (-\infin<k<+\infin)$

也可以看出频率点序号 $k$也是以 $N$为周期的，如果只取其一个周期，称之为 $\tilde X(k)$的主值序列：

$X(k) = \tilde X(k) | (0\leq k \leq N-1)$

主值序列 $X(k)$ 是一个长度为N的有限长离散频率序列。可见，离散时间周期序列在时域和频域的主值序列，均为有限长离散序列。且主值序列的长度均为 $N$（即 $n, k＝0,1,2,\cdots,N-1$）。

离散傅里叶变换：

在离散傅立叶级数（DFS）中，取其时域和频域的主值序列，变换仍然成立。这就是离散傅里叶变换（DFT），即：

$X(k) = DFT[x(n)] = \sum_{n=0}^{N-1}x(n)e^{-j\frac{2\pi}{N}kn},(k=0,1,2,\cdots,N-1)$

和其逆变换（IDFT）：
$x(n) = IDFT[X(k)] = \frac{1}{N}\sum_{k=0}^{N-1}X(k)e^{j\frac{2\pi}{N}kn}, (n=0,1,2,\cdots,N-1)$

可见离散傅里叶变换（DFT）只不过是特殊的离散傅立叶级数（DFS），就是对其时域和频域都仅取主值序列。

离散傅立叶级数（DFS）中的无限长序列和都是以 $N$为周期的周期序列，所以在计算离散时间周期序列及其频谱时，可以利用 DFS 的周期性，只需要在时域和频域各取一个主值序列，用计算机各计算一个周期中的 $N$个样值，最后将所得的主值序列 $x(n)$ 和 $X(k)$ 进行周期延拓，即可得到原来的无限长序列和。

由DFT的导入过程可以发现，DFT不仅可以解决无限长周期序列的计算机运算问题，而且更可以解决有限长序列的计算机运算问题。事实上，对于有限长离散序列，总可以把时域和频域的变换区间（序列长度）均取为 $N$（包括适当数量的补0点），通常把 $N$称之为等间隔采样点数，我们可以把这个 $N$点的变换区间视为某个周期序列的一个主值序列，直接利用DFT的定义计算其 $N$点变换。

3. 例子

1.单纯的从计算角度出发。
假设有一个序列长度 $N=4$，具体的 $x(n)={1,2,-1,3}, n=0,1,2,3$。

首先，由 $N=4$得到 ：

$W = e^{-j\frac{2\pi}{4}} = cos(\frac{2\pi}{2}) - j\cdot sin(\frac{\pi}{2}) = -j$

于是有，

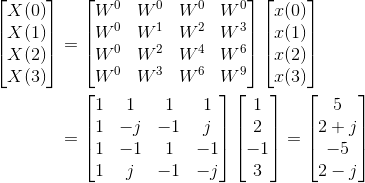
反变换：