https://medium.com/@andrew.chamberlain/the-linear-algebra-view-of-least-squares-regression-f67044b7f39b
线性回归是初学者学习的最重要的统计模型工具。然而，传统的教学方式使得我们很难理解到这个regression的本质。大多数课程聚焦在"计算"视图上，在这个计算视图中，regression关注于每个观察值和预测值之间差的平方和所形成的表达式，随后我们对这个表达式应用求导取0，最终算得各个系数的值。
大多数教科书诱导学生们关注在这个痛苦的计算过程上，随后依赖于类似R或者Stata的统计软件包上，这导致学生严重依赖于这些软件，而不会深入理解到底是怎么工作的，其本质是什么。。这往往是不真正理解数学的老师去教regression的常见方式。
在本文中，我将更优雅简单地演示LSR的本质，我把他称为"线性代数"视图。
问题导入
regression的终极目标是找到一个合适的model来拟合一系列观测值的集合。本例中，我搜集了一些工厂每天机器故障的次数，比如我已经获取了三个数据点(day, number of failure): (1,1),(2,2),(3,2)。
我们的目标是寻找到一个线性方程来拟合这三个点。我们相信存在一个数学映射，将"days"唯一映射为"failures"，或者说:
以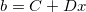 
的形式来映射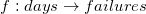
这里b就是每天的机器故障数, x是day, C,D是线性变换的系数，这也是我们要寻找的未知数。
我们将已知的三个数据点代入线性方程，得到:
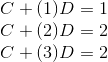
对于前两个点，model fit的非常好，但是第三个点却开始出现问题，也就是说我们已经意识到：这三个点并不在一条直线上，我们的model只能最大限度的近似它。
我们来看看如何以$Ax = b$的方式来表达我们的线性模型：
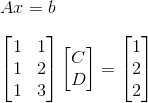
从这个矩阵中，我们可以说我们希望向量$\vec{b}$存在于矩阵$A$的列空间$C(A)$中.也就是说，我们希望通过矩阵A的列向量做线性组合能够得到我们的观测值$b$列向量。
然而，不幸的是，我们已经知道$b$本身并不能完全由A的列向量线性表示。这意味着向量$b$并不在$A$的列空间中.所以我们并不能通过解线性方程组的方式来求解到$x(C,D)$.
我们来继续通过画图来了解发生着什么。