高级数据结构 - 线段树、权值线段树（Java & JS & Python）

引子

现在给定一个数组 arr = [4, 7, 5, 3, 8, 9, 0, 1, 2, 6]，arr.length = n，无规律地多次进行如下操作：

• 查询arr指定区间 [l, r] 内最大值max
• 查询arr指定区间 [l, r] 内元素之和sum
• arr指定索引 i  位置的元素新增C 或者 覆盖为C
• arr指定区间 [l, r] 内每个元素值新增C 或者 覆盖为C

其中：

• 查询（区间最大值、区间和）的时间复杂度为O(n)
• 单值更新 的时间复杂度为O(1)
• 区间更新 的时间复杂度为O(n) 

如果需要多次求解arr的指定区间的和，则可以通过前缀和优化，具体可以看：

算法设计 - 前缀和 & 差分数列_伏城之外的博客-CSDN博客

但是上面需求中，arr数组是变化（单值更新，区间更新），因此arr数组的前缀和数组也是变化，每当arr发生更新时，则需要重新生成前缀和数组，这样的话就无法实现O(1)时间复杂度求区间和了。

如果说，执行m次的上面任意操作（每次操作都可以不一样），则最终时间复杂度为O(m * n)

那么有没有更高效的算法呢？

线段树概念

线段树是一种基于分治思想的二叉树，线段树的每个节点都对应arr数组的一个区间 [l, r]

• 线段树的叶子节点对应区间的 l == r
• 线段树的非叶子节点对应区间 [l, r] 的话，假设 mid = (l + r) / 2

1. 左子节点对应区间 [l, mid]
2. 右子节点对应区间 [mid + 1, r]

线段树的节点还会记录其对应区间 [l, r] 中的结果值，比如区间最大值、区间和。

即，我们可以认为线段树节点含有三个基础信息：

• 区间左边界 l
• 区间右边界 r
• 区间结果值 val

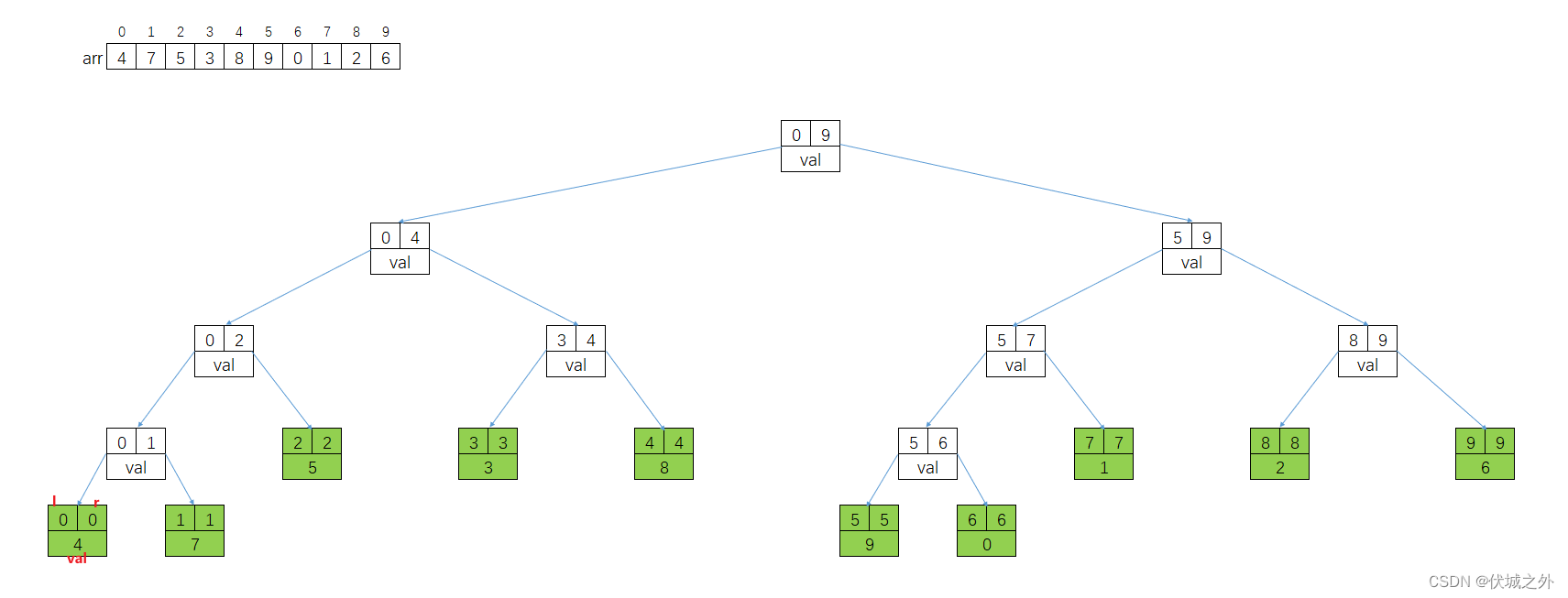
比如数组 arr = [4, 7, 5, 3, 8, 9, 0, 1, 2, 6]，对应的 线段树 图示如下：

其中线段树中叶子节点的 l==r，假设 i == l == r，则线段树叶子节点的值即为arr[i]。

如果我们需要求解区间最大值，则每个父节点的val相当于其两个子节点的val的较大者，因此可得线段树如下：

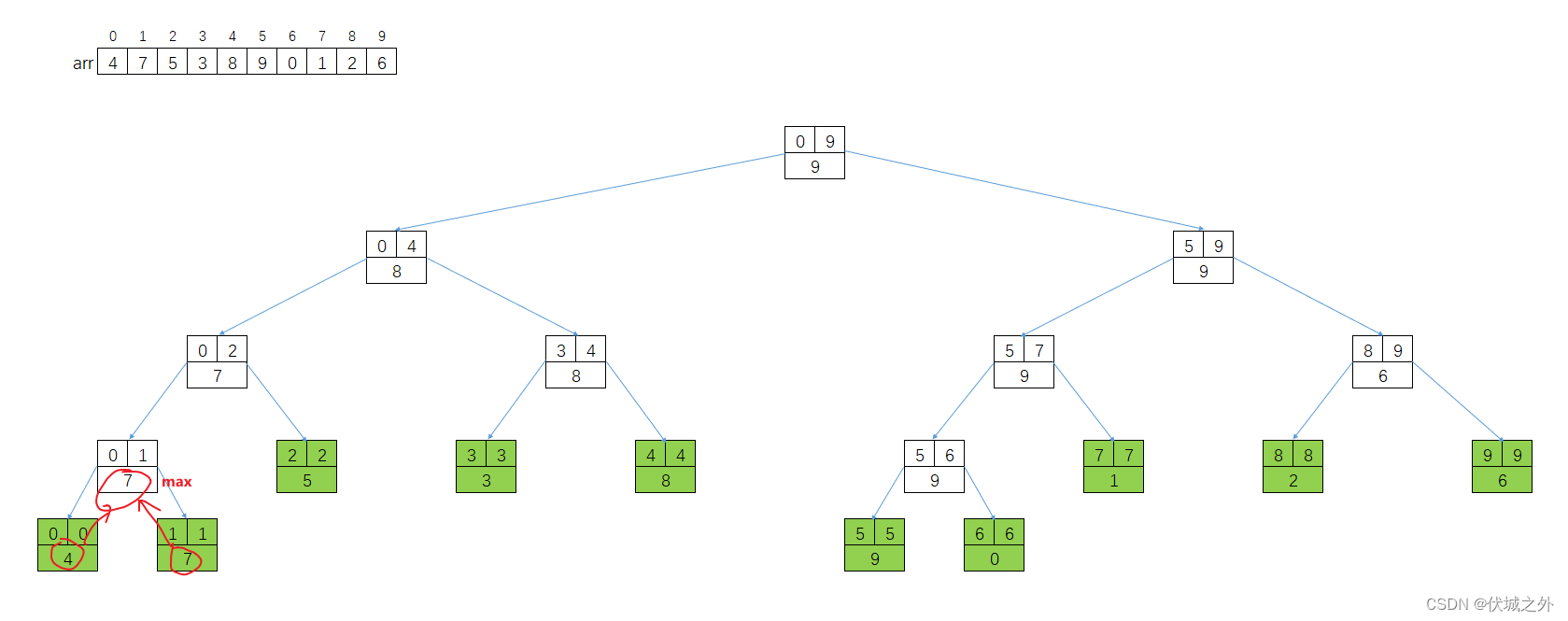
有了上面这个结构，我们就可以实现O(logN)的时间复杂度，找到任意区间的最大值。

比如，我们要找区间[3, 8]的最大值，则相当于从根节点开始分治，查找到[3, 4] 、[5, 7]、[8, 8] 三个区间结果值，从中取较大值作为[3, 8]区间的最大值。

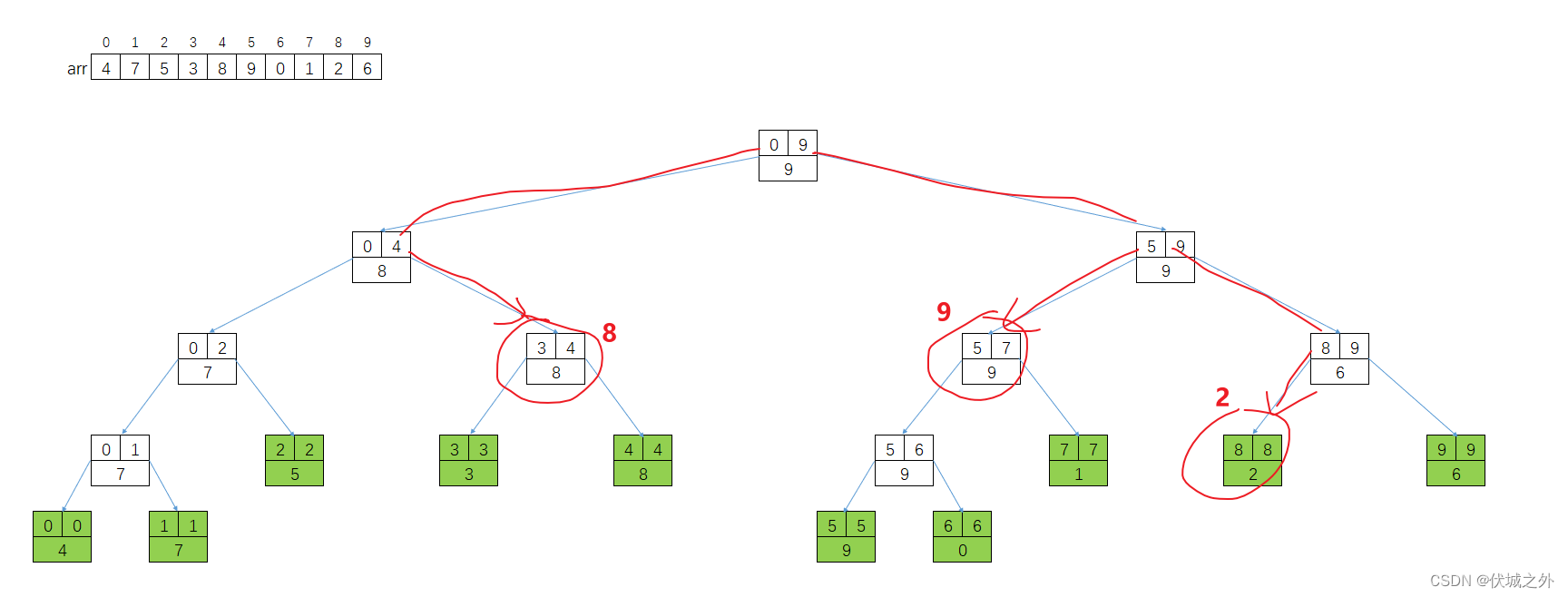
因此，基于线段树去查询区间信息是一种十分高效的策略。

线段树的底层容器

线段树其实就是一颗二叉树，且除了最后一层可能不满，其余层必然都是满的。

而对于满二叉树，我们可以用数组存储，比如下面图示的满二叉树：

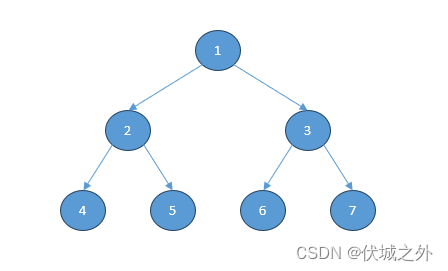
满二叉树中，如果父节点序号为k（k>=1），则其左子节点序号为2*k，右子节点序号为2*k+1

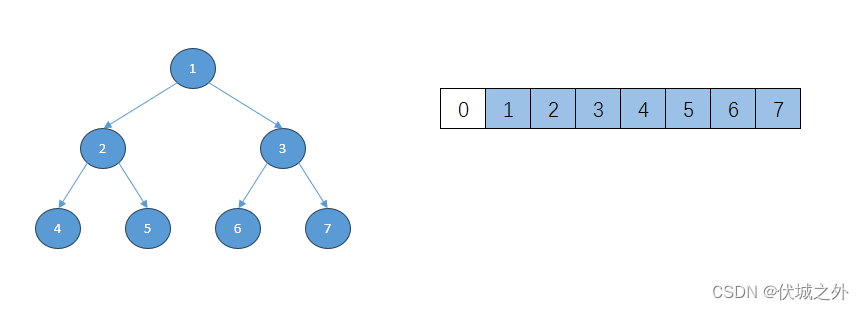
因此，如果将满二叉树结点序号  对应到  数组索引，则关系如上图所示。

即数组中 索引k  记录 满二叉树中 节点序号k的 节点值。 

因此，我们只要将线段树想象成满二叉树，即可存储进数组中，那么线段树需要申请多大长度的数组呢？

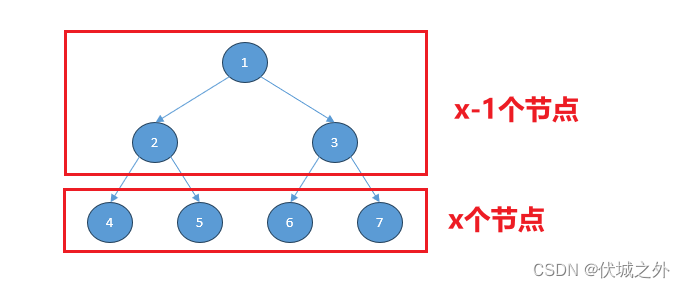
假设线段树描述的区间[l, r]长度为n，则说明线段树有n个叶子节点

那倒数第二层至多n个节点，而线段树的第1层~倒数第2层是一颗满二叉树，而对于满二叉树有如下性质：

满二叉树的最后一层有x个节点的话，则前面所有层节点数之和必然为x-1个。

证明也很容易，满二叉树的各层节点数：

第1层，有2^0个节点

第2层，有2^1个节点

第3层，有2^2个节点

....

假设只有3层的话，则必然有：2^0 + 2^1 = 2^2 - 1

如果线段树的倒数第2层至多n个节点，则线段树第1层~倒数第3层至多n-1个节点，

即线段树第1层~倒数第二层至多2n-1个节点。

那么线段树最后一层如果补满的话，必然至多是2n个节点。

因此线段树至多一共4n个节点，即只要开辟4n长度的数组空间，必然可以存储进线段树所有节点。

线段树的构建

线段树的底层容器是一个数组，我们假设为tree。

如果要被查询区间信息的原始数组arr的长度为n的话，则线段树的底层容器数组需要定义4n的长度。

tree数组元素 和 线段树节点的关系如下：

• tree数组元素 → 线段树节点。
• tree数组元素的索引 → 线段树节点的序号

而线段树的节点包含三个基本信息：

• 区间左边界 l
• 区间右边界 r
• 区间结果值 val（比如区间和，区间最值）

因此，我们可以定义一个Node类，来记录节点的信息。因此，tree数组也就是Node类型数组。

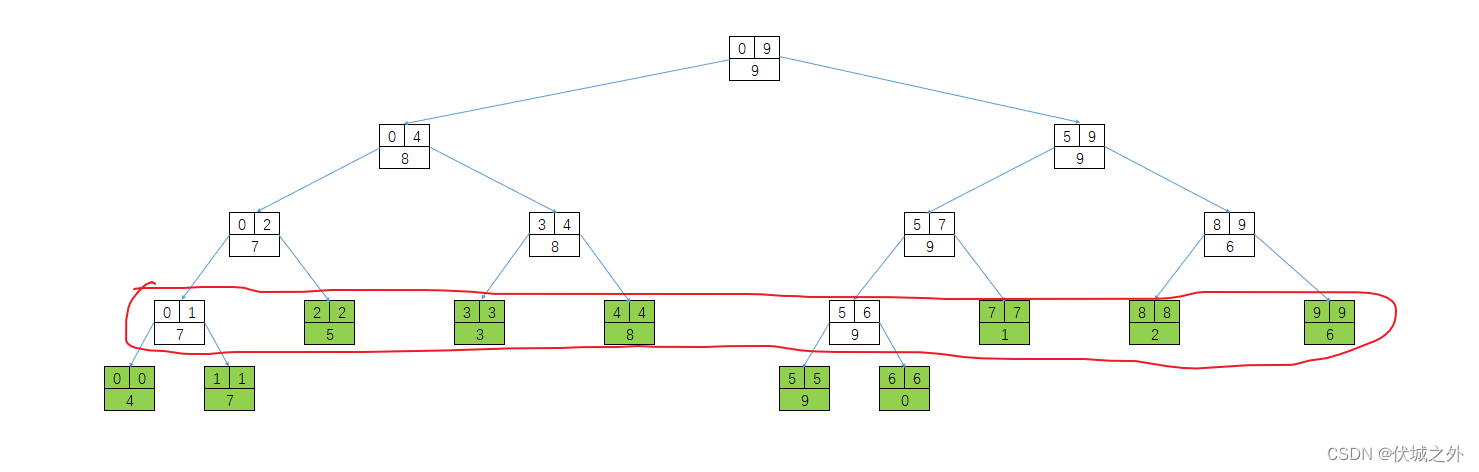
我们可以通过图示来看下tree数组的样子

构建线段树，即构建出上图中tree数组。

tree数组的索引k，也就是线段树节点的序号k。

tree[k] = Node {l, r, max}

上面伪代码的含义是：线段树节点k，对应于arr数组[l, r]区间，且记录了该区间内最大值max

我们可以通过分治递归的方式完成线段树的构建。

比如我们已经知道了 k=1的线段树节点，维护的arr区间是[0, 9]，目前需要求解该区间的最大值？

由于线段是一个基于分治思想的二叉树，因此可以将[0, 9]区间二分，变成[0, 4]，和 [5, 9]

即，将[0, 9]区间最大值的问题，变为了[0, 4]区间最大值和[5, 9]区间最大值的两个规模更小的子问题。

而[0, 4]区间刚好是k=2节点维护的区间，[5, 9]是k=3节点维护的区间。

之后，继续按照此逻辑，递归求解[0, 4]和[5, 9]区间最值。

直到，被二分后的区间的 l == r，即到达了叶子节点时，此时区间[l, r]的最大值，就是arr[l]或arr[r]，然后可以开始回溯。

回溯过程中，父节点的区间最大值  等于 其两个节点区间最大值的较大者。

具体代码实现如下（含测试代码）：

JS代码实现

// 线段树节点定义
class Node {
  constructor(l, r) {
    this.l = l; // 区间左边界
    this.r = r; // 区间右边界
    this.max = undefined; // 区间内最大值
  }
}

// 线段树定义
class SegmentTree {
  constructor(arr) {
    // arr是要执行查询区间最大值的原始数组
    this.arr = arr;
    // 线段树底层数据结构，其实就是一个数组，我们定义其为tree，如果arr数组长度为n，则tree数组需要4n的长度
    this.tree = new Array(arr.length * 4);
    // 从根节点开始构建，线段树根节点序号k=1，对应的区间范围是[0, arr.length-1]
    this.build(1, 0, arr.length - 1);
  }

  /**
   * 线段树构建
   * @param {*} k 线段树节点序号
   * @param {*} l 节点对应的区间范围左边界
   * @param {*} r 节点对应的区间范围右边界
   */
  build(k, l, r) {
    // 初始化线段树节点, 即建立节点序号k和区间范围[l, r]的联系
    this.tree[k] = new Node(l, r);

    // 如果l==r, 则说明k节点是线段树的叶子节点
    if (l == r) {
      // 而线段树叶子节点的结果值就是arr[l]或arr[r]本身
      this.tree[k].max = arr[r];
      // 回溯
      return;
    }

    // 如果l!=r, 则说明k节点不是线段树叶子节点，因此其必有左右子节点，左右子节点的分界位置是mid
    const mid = (l + r) >> 1; // 等价于Math.floor((l + r) / 2)

    // 递归构建k节点的左子节点，序号为2 * k，对应区间范围是[l, mid]
    this.build(2 * k, l, mid);
    // 递归构建k节点的右子节点，序号为2 * k + 1，对应区间范围是[mid+1, r]
    this.build(2 * k + 1, mid + 1, r);

    // k节点的结果值，取其左右子节点结果值的较大值
    this.tree[k].max = Math.max(this.tree[2 * k].max, this.tree[2 * k + 1].max);
  }
}

// 测试
const arr = [4, 7, 5, 3, 8, 9, 0, 1, 2, 6];

const tree = new SegmentTree(arr).tree;

console.log("k\t| tree[k]");
for (let k = 0; k < tree.length; k++) {
  if (tree[k]) {
    console.log(
      `${k}\t| Node{ l: ${tree[k].l}, r: ${tree[k].r}, max: ${tree[k].max}}`
    );
  } else {
    console.log(`${k}\t| null`);
  }
}

Java代码实现

// 线段树定义
public class SegmentTree {
  // 线段树节点定义
  static class Node {
    int l; // 区间左边界
    int r; // 区间右边界
    int max; // 区间内最大值

    public Node(int l, int r) {
      this.l = l;
      this.r = r;
    }
  }

  int[] arr;

  Node[] tree;

  public SegmentTree(int[] arr) {
    // arr是要执行查询区间最大值的原始数组
    this.arr = arr;
    // 线段树底层数据结构，其实就是一个数组，我们定义其为tree，如果arr数组长度为n，则tree数组需要4n的长度
    this.tree = new Node[arr.length * 4];
    // 从根节点开始构建，线段树根节点序号k=1，对应的区间范围是[0, arr.length-1]
    this.build(1, 0, arr.length - 1);
  }

  /**
   * 线段树构建
   *
   * @param k 线段树节点序号
   * @param l 节点对应的区间范围左边界
   * @param r 节点对应的区间范围右边界
   */
  private void build(int k, int l, int r) {
    // 初始化线段树节点, 即建立节点序号k和区间范围[l, r]的联系
    this.tree[k] = new Node(l, r);

    // 如果l==r, 则说明k节点是线段树的叶子节点
    if (l == r) {
      // 而线段树叶子节点的结果值就是arr[l]或arr[r]本身
      this.tree[k].max = this.arr[r];
      // 回溯
      return;
    }

    // 如果l!=r, 则说明k节点不是线段树叶子节点，因此其必有左右子节点，左右子节点的分界位置是mid
    int mid = (l + r) >> 1;

    // 递归构建k节点的左子节点，序号为2 * k，对应区间范围是[l, mid]
    this.build(2 * k, l, mid);
    // 递归构建k节点的右子节点，序号为2 * k + 1，对应区间范围是[mid+1, r]
    this.build(2 * k + 1, mid + 1, r);

    // k节点的结果值，取其左右子节点结果值的较大值
    this.tree[k].max = Math.max(this.tree[2 * k].max, this.tree[2 * k + 1].max);
  }

  // 测试
  public static void main(String[] args) {
    int[] arr = {4, 7, 5, 3, 8, 9, 0, 1, 2, 6};

    Node[] tree = new SegmentTree(arr).tree;

    System.out.println("k\t| tree[k]");
    for (int k = 0; k < tree.length; k++) {
      if (tree[k] == null) {
        System.out.println(k + "\t| null");
      } else {
        System.out.println(
            k + "\t| Node{ l: " + tree[k].l + ", r: " + tree[k].r + ", max: " + tree[k].max + "}");
      }
    }
  }
}

Python代码实现

# 线段树节点定义
class Node:
    def __init__(self):
        self.l = None
        self.r = None
        self.mx = None


# 线段树定义
class SegmentTree:
    def __init__(self, lst):
        # lst是要执行查询区间最大值的原始数组
        self.lst = lst
        # 线段树底层数据结构，其实就是一个数组，我们定义其为tree，如果lst数组长度为n，则tree数组需要4n的长度
        self.tree = [Node() for _ in range(len(lst) * 4)]
        # 从根节点开始构建，线段树根节点序号k=1，对应的区间范围是[0, len(lst) - 1]
        self.build(1, 0, len(lst) - 1)

    def build(self, k, l, r):
        """
        线段树构建
        :param k: 线段树节点序号
        :param l: 节点对应的区间范围左边界
        :param r: 节点对应的区间范围右边界
        """

        # 初始化线段树节点, 即建立节点序号k和区间范围[l, r]的联系
        self.tree[k].l = l
        self.tree[k].r = r

        # 如果l==r, 则说明k节点是线段树的叶子节点
        if l == r:
            # 而线段树叶子节点的结果值就是lst[l]或lst[r]本身
            self.tree[k].mx = self.lst[r]
            # 回溯
            return

        # 如果l!=r, 则说明k节点不是线段树叶子节点，因此其必有左右子节点，左右子节点的分界位置是mid
        mid = (l + r) >> 1

        # 递归构建k节点的左子节点，序号为2 * k，对应区间范围是[l, mid]
        self.build(2 * k, l, mid)
        # 递归构建k节点的右子节点，序号为2 * k + 1，对应区间范围是[mid+1, r]
        self.build(2 * k + 1, mid + 1, r)

        # k节点的结果值，取其左右子节点结果值的较大值
        self.tree[k].mx = max(self.tree[2 * k].mx, self.tree[2 * k + 1].mx)


# 测试代码
lst = [4, 7, 5, 3, 8, 9, 0, 1, 2, 6]
print("k\t| tree[k]")
for k, node in enumerate(SegmentTree(lst).tree):
    if node.mx:
        print(f"{k}\t| Node[ l: {node.l}, r: {node.r}, mx: {node.mx} ]")
    else:
        print(f"{k}\t| null")

查询任意区间结果值