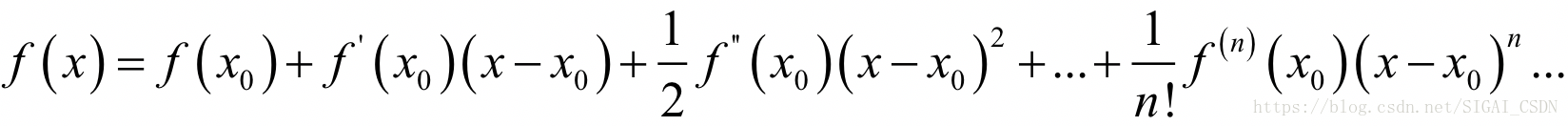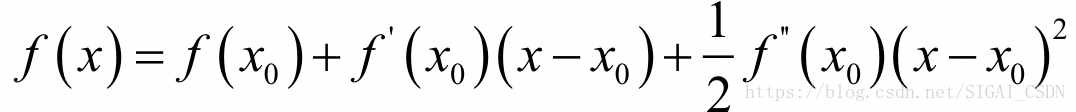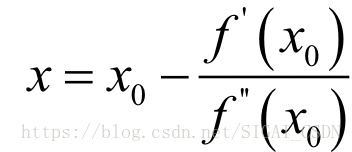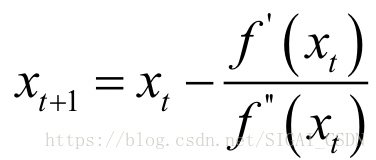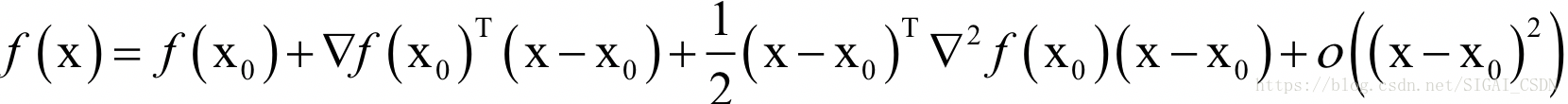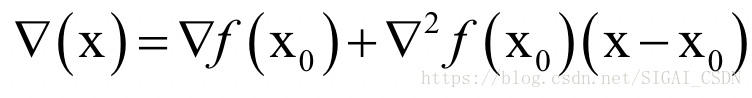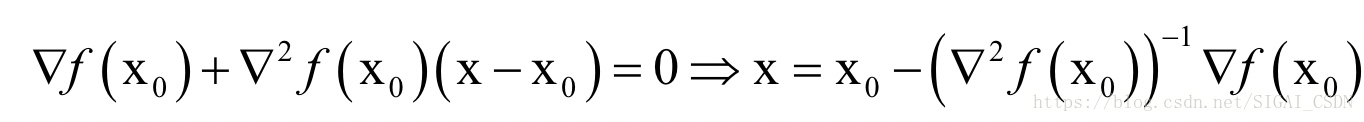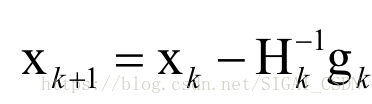原创声明：本文为 SIGAI 原创文章，仅供个人学习使用，未经允许，不能用于商业目的。
导言
牛顿法是数值优化算法中的大家族，她和她的改进型在很多实际问题中得到了应用。在机器学习中，牛顿法是和梯度下降法地位相当的的主要优化算法。在本文中，SIGAI将为大家深入浅出的系统讲述牛顿法的原理与应用。
牛顿法的起源
牛顿法以伟大的英国科学家牛顿命名，牛顿不仅是伟大的物理学家，是近代物理的奠基人，还是伟大的数学家，他和德国数学家莱布尼兹并列发明了微积分，这是数学历史上最有划时代意义的成果之一，奠定了近代和现代数学的基石。在数学中，也有很多以牛顿命名的公式和定理，牛顿法就是其中之一。
牛顿法不仅可以用来求解函数的极值问题，还可以用来求解方程的根，二者在本质上是一个问题，因为求解函数极值的思路是寻找导数为0的点，这就是求解方程。在本文中，我们介绍的是求解函数极值的牛顿法。
在SIGAI之前关于最优方法的系列文章“理解梯度下降法”，“理解凸优化”中，我们介绍了最优化的基本概念和原理，以及迭代法的思想，如果对这些概念还不清楚，请先阅读这两篇文章。和梯度下降法一样，牛顿法也是寻找导数为0的点，同样是一种迭代法。核心思想是在某点处用二次函数来近似目标函数，得到导数为0的方程，求解该方程，得到下一个迭代点。因为是用二次函数近似，因此可能会有误差，需要反复这样迭代，直到到达导数为0的点处。下面我们开始具体的推导，先考虑一元函数的情况，然后推广到多元函数。
一元函数的情况
为了能让大家更好的理解推导过程的原理，首先考虑一元函数的情况。根据一元函数的泰勒展开公式，我们对目标函数在x0点处做泰勒展开，有：
如果忽略2次以上的项，则有：
现在我们在x0点处，要以它为基础，找到导数为0的点，即导数为0。对上面等式两边同时求导，并令导数为0，可以得到下面的方程：
可以解得：
这样我们就得到了下一点的位置，从而走到x1。接下来重复这个过程，直到到达导数为0的点，由此得到牛顿法的迭代公式：
给定初始迭代点x0，反复用上面的公式进行迭代，直到达到导数为0的点或者达到最大迭代次数。
多元函数的情况
下面推广到多元函数的情况，如果读者对梯度，Hessian的概念还不清楚，请先去看微积分教材，或者阅读SIGAI之前关于最优化的公众号文章。根据多元函数的泰勒展开公式，我们对目标函数在x0点处做泰勒展开，有：
忽略二次及以上的项，并对上式两边同时求梯度，得到函数的导数（梯度向量）为：
其中
这是一个线性方程组的解。如果将梯度向量简写为g，上面的公式可以简写为：
从初始点x0处开始，反复计算函数在处的Hessian矩阵和梯度向量，然后用下述公式进行迭代：
最终会到达函数的驻点处。其中
实现细节
根据上面的推导，我们可以得到牛顿法的完整流程为：
其中
如果我们把步长设置的足够大（在这里为1），则算法一步就收敛了。在这里，初始迭代位置为(0,4)，最优解为(0,0)。
对于不带约束条件的问题，我们可以将x的初始值设定为任意值，最简单的，可以设置为全0的向量。迭代终止的判定规则和梯度下降法相同，是检查梯度是否接近于0。
牛顿法并不能保证每一步迭代时函数值下降，也不保证一定收敛。为此，提出了一些补救措施，其中的一种是直线搜索（line search）技术，即搜索最优步长。具体做法是让
和梯度下降法相比牛顿法有更快的收敛速度，但每一步迭代的成本也更高。在每次迭代中，除了要计算梯度向量还要计算Hessian矩阵，并求解Hessian矩阵的逆矩阵。实际实现时一般不直接求Hessian矩阵的逆矩阵，而是求解如下方程组：
求解这个线性方程组一般使用迭代法，如共轭梯度法，当然也可以使用其他算法。
面临的问题
和梯度下降法一样，牛顿法寻找的也是导数为0的点，这不一定是极值点，因此会面临局部极小值和鞍点问题，这在之前的文章中已经介绍过了，这里不再重复。
牛顿法面临的另外一个问题是Hessian矩阵可能不可逆，从而导致这种方法失效。此外，求解Hessian矩阵的逆矩阵或者求解线性方程组计算量大，需要耗费大量的时间。为此，提出了拟牛顿法这种改进方案，在后面会介绍。
除此之外，牛顿法在每次迭代时序列xi可能不会收敛到一个最优解，它甚至不能保证函数值会按照这个序列递减。解决第一个问题可以通过调整牛顿方向的步长来实现，目前常用的方法有两种：直线搜索和可信区域法。可信域牛顿法在后面也会介绍。
可信域牛顿法
可信域牛顿法（Trust Region Newton Methods）可以求解带界限约束的最优化问题，是对牛顿法的改进。在可信域牛顿法的每一步迭代中，有一个迭代序列
这个式子可以通过泰勒展开得到，忽略二次以上的项，这是对函数下降值：
的近似。算法寻找一个
这是函数值的实际减少量和二次近似模型预测方向导致的函数减少量的比值。迭代方向可以接受的条件是
其中
而
可行域的边界
在牛顿法的每一步迭代中，动态调整可信域，确保序列收敛。
拟牛顿法
牛顿法在每次迭代时需要计算出Hessian矩阵，然后求解一个以该矩阵为系数矩阵的线性方程组，这非常耗时，另外Hessian矩阵可能不可逆。为此提出了一些改进的方法，典型的代表是拟牛顿法（Quasi-Newton）。
拟牛顿法的思想是不计算目标函数的Hessian矩阵然后求逆矩阵，而是通过其他手段得到Hessian矩阵或其逆矩阵的近似矩阵。具体做法是构造一个近似Hessian矩阵或其逆矩阵的正定对称矩阵，用该矩阵进行牛顿法的迭代。将函数在点处进行泰勒展开，忽略二次以上的项，有：
这个条件称为拟牛顿条件，用来近似代替Hessian矩阵的矩阵需要满足此条件。根据此条件，构造出了多种拟牛顿法，典型的有DFP算法、BFGS算法、L-BFGS算法等，在这里我们重点介绍BFGS算法。下图列出了常用的拟牛顿法的迭代公式（图片来自维基百科）：
BFGS算法是它的四个发明人Broyden，Fletcher，Goldfarb和Shanno名字首字母的简写。算法的思想是构造Hessian矩阵的近似矩阵：
算法的完整流程为：
实际应用
下面介绍牛顿法在机器学习中的实际应用。在这里我们以线性支持向量机和liblinear为例。liblinear是一个线性算法的开源库，其作者是台湾大学林智仁教授和他的学生，与libsvm的作者相同。这个库支持logistic回归和线性支持向量机两类算法，包括各种损失函数和正则化的版本。L1正则化L2损失函数线性支持向量机训练时求解如下最优化问题：
目标函数的前半部分其中为L1范数的正则化项，后半部分括号里为合页损失函数。在liblinear中，求解上述问题采用了坐标下降法，这是一种分治法，每次挑选出一部分变量进行优化，将其他变量固定住不动。如果只挑选出一个变量进行优化，要求解的子问题为：
其中向量的第个分量为1，其他分量全为0。上式中最后一步对函数用二阶泰勒展开近似代替。上面子问题的求解采用牛顿法。求解整个问题的坐标下降法流程为（这里只列出了和牛顿法相关的步骤）：
设置各个参数的初始值 如果w还不是最优值，则循环 循环，对j = 1, 2, ..., n 求解如下问题得到牛顿方向d： 更新参数值： 结束循环 结束循环
下面来看源代码实现。函数solve_l1r_l2_svc实现求解L1正则化L2损失函数支持向量机原问题的坐标下降法。在这里我们重点看牛顿方向的计算，直线搜索，参数更新这三步，其他的可以忽略掉。代码如下：
static void solve_l1r_l2_svc(problem *prob_col, double *w, double eps, double Cp,
double Cn)
{
int l = prob_col->l;
int w_size = prob_col->n;
int j, s, iter = 0;
int max_iter = 1000;
int active_size = w_size;
int max_num_linesearch = 20;
double sigma = 0.01;
double d, G_loss, G, H;
double Gmax_old = INF;
double Gmax_new, Gnorm1_new;
double Gnorm1_init = -1.0; // Gnorm1_init is initialized at the first iteration
double d_old, d_diff;
double loss_old, loss_new;
double appxcond, cond;
int *index = new int[w_size];
schar *y = new schar[l];
double *b = new double[l]; // b = 1-ywTx
double *xj_sq = new double[w_size];
feature_node *x;
double C[3] = {Cn,0,Cp};
// w赋初值
for(j=0; j<w_size; j++)
w[j] = 0;
for(j=0; j<l; j++)
{
b[j] = 1;
if(prob_col->y[j] > 0)
y[j] = 1;
else
y[j] = -1;
}
for(j=0; j<w_size; j++)
{
index[j] = j;
xj_sq[j] = 0;
x = prob_col->x[j];
while(x->index != -1)
{
int ind = x->index-1;
x->value *= y[ind]; // x->value stores yi*xij
double val = x->value;
b[ind] -= w[j]*val;
xj_sq[j] += C[GETI(ind)]*val*val;
x++;
}
}
// 这是坐标下降法的核心，循环迭代，直到收敛
while(iter < max_iter)
{
Gmax_new = 0;
Gnorm1_new = 0;
// 先对优化变量的下标进行随机洗牌
for(j=0; j<active_size; j++)
{
int i = j+rand()%(active_size-j);
swap(index[i], index[j]);
}
// 依次对每个变量进行优化
for(s=0; s<active_size; s++)
{
j = index[s];
G_loss = 0;
H = 0;
x = prob_col->x[j];
while(x->index != -1)
{
int ind = x->index-1;
if(b[ind] > 0)
{
double val = x->value;
double tmp = C[GETI(ind)]*val;
G_loss -= tmp*b[ind];
H += tmp*val;
}
x++;
}
G_loss *= 2;
G = G_loss;
H *= 2;
H = max(H, 1e-12);
double Gp = G+1;
double Gn = G-1;
double violation = 0;
if(w[j] == 0)
{
if(Gp < 0)
violation = -Gp;
else if(Gn > 0)
violation = Gn;
else if(Gp>Gmax_old/l && Gn<-Gmax_old/l)
{
active_size--;
swap(index[s], index[active_size]);
s--;
continue;
}
}
else if(w[j] > 0)
violation = fabs(Gp);
else
violation = fabs(Gn);
Gmax_new = max(Gmax_new, violation);
Gnorm1_new += violation;
// 确定牛顿方向d
if(Gp < H*w[j])
d = -Gp/H;
else if(Gn > H*w[j])
d = -Gn/H;
else
d = -w[j];
if(fabs(d) < 1.0e-12)
continue;
double delta = fabs(w[j]+d)-fabs(w[j]) + G*d;
d_old = 0;
int num_linesearch;
// 直线搜索过程
for(num_linesearch=0; num_linesearch < max_num_linesearch;
num_linesearch++)
{
d_diff = d_old - d;
cond = fabs(w[j]+d)-fabs(w[j]) - sigma*delta;
appxcond = xj_sq[j]*d*d + G_loss*d + cond;
if(appxcond <= 0)
{
x = prob_col->x[j];
while(x->index != -1)
{
b[x->index-1] += d_diff*x->value;
x++;
}
break;
}
if(num_linesearch == 0)
{
loss_old = 0;
loss_new = 0;
x = prob_col->x[j];
while(x->index != -1)
{
int ind = x->index-1;
if(b[ind] > 0)
loss_old += C[GETI(ind)]*b[ind]*b[ind];
double b_new = b[ind] + d_diff*x->value;
b[ind] = b_new;
if(b_new > 0)
loss_new += C[GETI(ind)]*b_new*b_new;
x++;
}
}
else
{
loss_new = 0;
x = prob_col->x[j];
while(x->index != -1)
{
int ind = x->index-1;
double b_new = b[ind] + d_diff*x->value;
b[ind] = b_new;
if(b_new > 0)
loss_new += C[GETI(ind)]*b_new*b_new;
x++;
}
}
cond = cond + loss_new - loss_old;
if(cond <= 0)
break;
else
{
d_old = d;
d *= 0.5;
delta *= 0.5;
}
}
w[j] += d;
if(num_linesearch >= max_num_linesearch)
{
info("#");
for(int i=0; i<l; i++)
b[i] = 1;
for(int i=0; i<w_size; i++)
{
if(w[i]==0) continue;
x = prob_col->x[i];
while(x->index != -1)
{
b[x->index-1] -= w[i]*x->value;
x++;
}
}
}
}
if(iter == 0)
Gnorm1_init = Gnorm1_new;
iter++;
if(iter % 10 == 0)
info(".");
if(Gnorm1_new <= eps*Gnorm1_init)
{
if(active_size == w_size)
break;
else
{
active_size = w_size;
info("*");
Gmax_old = INF;
continue;
}
}
Gmax_old = Gmax_new;
}
info("\noptimization finished, #iter = %d\n", iter);
if(iter >= max_iter)
info("\nWARNING: reaching max number of iterations\n");
// 计算目标函数值
double v = 0;
int nnz = 0;
for(j=0; j<w_size; j++)
{
x = prob_col->x[j];
while(x->index != -1)
{
x->value *= prob_col->y[x->index-1]; // restore x->value
x++;
}
if(w[j] != 0)
{
v += fabs(w[j]);
nnz++;
}
}
for(j=0; j<l; j++)
if(b[j] > 0)
v += C[GETI(j)]*b[j]*b[j];
info("Objective value = %lf\n", v);
info("#nonzeros/#features = %d/%d\n", nnz, w_size);
delete [] index;
delete [] y;
delete [] b;
delete [] xj_sq;
}
原创声明：本文为 SIGAI 原创文章，仅供个人学习使用，未经允许，不能用于商业目的。
推荐阅读
[1] 机器学习-波澜壮阔40年 SIGAI 2018.4.13.
[2] 学好机器学习需要哪些数学知识？SIGAI 2018.4.17.
[3] 人脸识别算法演化史 SIGAI 2018.4.20.
[4] 基于深度学习的目标检测算法综述 SIGAI 2018.4.24.
[5] 卷积神经网络为什么能够称霸计算机视觉领域？ SIGAI 2018.4.26.
[6] 用一张图理解SVM的脉络 SIGAI 2018.4.28.
[7] 人脸检测算法综述 SIGAI 2018.5.3.
[8] 理解神经网络的激活函数 SIGAI 2018.5.5.
[9] 深度卷积神经网络演化历史及结构改进脉络-40页长文全面解读 SIGAI 2018.5.8.
[10] 理解梯度下降法 SIGAI 2018.5.11
[11] 循环神经网络综述—语音识别与自然语言处理的利器 SIGAI 2018.5.15
[12] 理解凸优化 SIGAI 2018.5.18
[13]【实验】理解SVM的核函数和参数 SIGAI 2018.5.22
[14] ] [SIGAI综述] 行人检测算法 SIGAI 2018.5.25
[15] 机器学习在自动驾驶中的应用—以百度阿波罗平台为例 SIGAI 2018.5.29
