公钥密码学中的简单数学基础

公钥密码学中的简单数学基础

本文基于《深入浅出密码学》第六章以及Paillier中使用到的相关数学知识进行总结，并计划不断更新

逆元

介绍

注意：不是所有的元素都存在乘法逆元

假设$a\in Z_m$，乘法逆元 $a^{-1}$ 定义为:$a\cdot a^{-1}\equiv 1(\mathrm{mod}m)$

如果一个元素a的逆元存在，则可以除以这个元素，因为$b/a\equiv b\cdot a^{-1}(\mathrm{mod}m)$

判断

当且仅当 $gcd(a,m)=1$，一个元素$a\in Z$ 存在乘法逆元 $a^{-1}$ ，即两数互质。

寻找

寻找元素的逆元比较困难，通常使用拓展欧几里得算法（见下）

应用

在 RSA 密码体系中会在选择公开指数 e 时保证 $gcd(e,\phi (n))=1$，是为了保证 e 的逆元存在，即保证私钥始终存在，$d\cdot e\equiv 1\mathrm{mod}\phi (n)$

欧拉定理

假设 $a$ 和 $m$ 都是整数，且 $gcd(a,m)=1$，则 $a^{\phi (m)}\equiv 1(\mathrm{mod}m)$

由于这个定理对模数 m 使适用，所以它也适用于整数环${\mathbb{Z}}_m$内的所有整数

补充

• 对质数 $p$ ，$\varphi (p)=p-1$
• 带有幂次素数的欧拉函数：若 $p$ 为素数，且有 $n=p^r$,则 $\phi (n)=\phi (p^r)=p^{r-1}\phi (p-1)$【易于证明将其中p倍数都去除即可】
• 设 $m=pq$，若 $p$ 和 $q$ 互素且大于1，则$\phi (m)=\phi (p)\phi (q)$【易于证明因为两者互素】

应用

常应用于高指数求模的化简运算

例如：$2^{1000000}(\mathrm{mod}7)$

结合欧拉定理：$2^{\phi (7)}\equiv 2^6\equiv 1(\mathrm{mod}7)$

以及1000000=166666*6+4

所以：$2^{1000000}\equiv (2^6{)}^{166666}\cdot 2^4\equiv 2(\mathrm{mod}7)$

费马小定理

假设 $a$ 为一个整数，$p$ 为一个素数，则 $a^p\equiv a(\mathrm{mod}p)$

费马小定理是欧拉定理的一个特例，如果 $p$ 为一个素数，则 $\phi (p)=p-1$ 成立。如果将这个值用于欧拉定理，则可得到：$a^{\phi (p)}=a^{p-1}\equiv 1(\mathrm{mod}m)$

欧几里得算法

介绍

两个正整数 $r_0$ 和 $r_1$ 的最大公约数 $gcd$ 表示为：$gcd(r_0,r_1)$

对于小整数而言，最大公约数的计算非常容易就是将两个整数因式分解，并找出最大的公共因子。然而，对于公钥中的大整数而言，因式分解通常是不可能的，所以人们通常使用一种更有效的算法计算 $gcd$ ，那就是欧几里得算法。

原理

这里使用的基础原理是 $gcd(r_0,r_1)=gcd(r_0-r_1,r_1)$

证明如下：假设 $gcd(r_0,r_1)=g$ ，由于g可以同时除 $r_0$ 与 $r_1$ ，则可以记为 $r_0=g\cdot x$ 和 $r_1=g\cdot y$ ，其中 $x>y$ 且x与y为互素的整数，即他们没有公共因子，则有$gcd(r_0-r_1,r_1)=gcd(g\cdot (x-y),g\cdot y)=g$

运算

我们可以迭代的使用上述过程，从而化简运算：

$gcd(r_0,r_1)=gcd(r_0-r_1,r_1)=gcd(r_0-2r_1,r_1)=gcd(r_0-3r_1,r_1)=\cdots =gcd(r_0-m{r}_1,r_1)$

即可以表示为：$gcd(r_{0}mod{r}_1,r_1)$

由于第一项比第二项小，通常可以交换它们：$gcd(r_1,r_{0}mod{r}_1)$

在整个过程中，我们可以将查找两个给定整数的最大公约数化简为查找两个较小整数的最大公约数，迭代直至最后获得 $gcd(r_l,0)=r_l$，而这实际上也就是原始问题的答案

例如：计算 $gcd(27,21)$

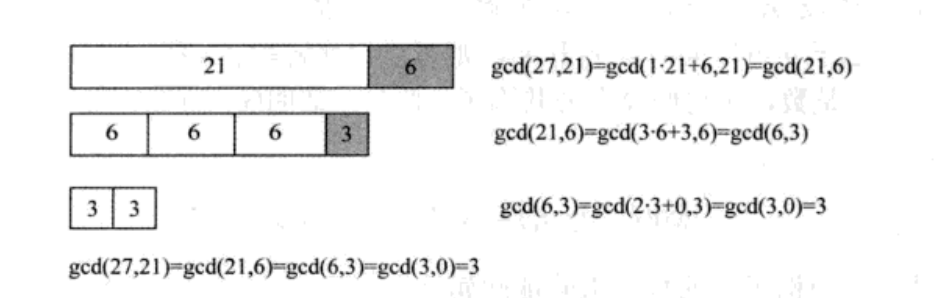
即使是处理非常大的数，欧几里得算法依然高效，迭代次数与输入系统操作数的位数有紧密关系，这意味着如果一个 $gcd$ 涉及的数字都是1024位，则此 $gcd$ 的迭代次数就是1024乘以一个常数（当然只有几千次迭代的算法在当今PC上很容易实现，该算法在实际上效率极高）

拓展欧几里得算法(EEA)

思路

执行标准的欧几里得算法，但将每轮迭代中的余数 $r_i$ 表示为以下形式的线性组合: $r_1=s_i\cdot r_0+t_i\cdot r_1$

那么最后一轮迭代对应的等式为：$r_1=gcd(r_0,r_1)=s_i\cdot r_0+t_i\cdot r_1=s{r}_0+t{r}_1$

这也意味着最后的系数 $s_l$ 也是等式所寻找的系数 $s$，同时 $t_l=t$

例如：计算 $r_0=973$ $r_1=301$

i	$r_{i-2}=q_{i-1}+r_i$	$r_i=[s_i]r_0+[t_i]r_1$
1	$973=3\cdot 301+70$	$70=[1]r_0+[-3]r_1$
2	$301=4\cdot 70+21$	$21=301-4\cdot 70=r_1-4(1r_0-3r_1)=[-4]r_0+[13]r_1$
3	$70=3\cdot 21+7$	$7=70-3\cdot 21=(1r_0-3r_1)-3(-4r_0+13r_1)=[13]r_0+[-42]r_1$
4	$21=3\cdot 7+0$

上述过程计算了三个参数，即 $gcd(973,301)=7$，$s=13$ 及 $t=-42$

应用

计算线性组合

计算线性组合：$gcd(r_0,r_1)=s\cdot r_0+t\cdot r_1$ 其中 s 与 t 均表示整型系数

求逆元

EEA在非对称密码学中的主要应用就是计算整数的逆元

计算 $r_{1}mod{r}_0$ 的逆元$(r_1<r_0)$

由上述可知，只有当 $gcd(r_0,r_1)=1$ 的情况下逆元才存在。

由EEA可得： $s_i\cdot r_0+t_i\cdot r_1=1=gcd(r_0,r_1)$

计算：

$s\cdot r_0+t\cdot r_1=1$

$s\cdot 0+t\cdot r_1\equiv 1mod{r}_0$

$r_1\cdot t\equiv 1mod{r}_0$

即 $t$ 本身就是 $r_1$ 的逆元：$t=r_1^{-1}mod{r}_0$

综上，计算逆元 $a^{-1}modm$ ，直接使用输入参数为 $m$ 和 $a$ 的 EEA 即可，计算出来的输出值 t 即为其逆元

举例说明，计算 $12^{-1}mod67$ 的计算过程如下：

$i$	$q_{i-1}$	$r_i$	$s_i$	$t_i$
2	5	7	1	-5
3	1	5	-1	6
4	1	2	2	-11
5	2	1	-5	28

即 12 的逆元为$12^{-1}\equiv 28mod67$

注意：一般不需要系数 s ，实际中也不计算该值。该结果可能 t 是负数，这种情况下我们需要计算 $t=t+r_0$

计算伽罗瓦域内的乘法逆元

与 AES 中的S-盒起源以及椭圆曲线公钥加密算法有关，EEA可以完全当做多项式（而不是整数）使用。如果想要计算有限域$GF(2^m)$ 中

的一个逆元，算法的输入就是域元素 $A(x)$ 和不可约多项式 $P(x)$，由于 $P(x)$ 是不可约多项式，所以 $gcd$ 总是等于 1。即：

$s(x)P(x)+t(x)A(x)=gcd(P(x),A(x))=1$

同理：$t(x)\equiv A^{-1}(x)modP(x)$

举例计算基于$P(x)=x^3+x+1$ 的有限域 $GF(2^3)$ 中 $A(x)=x^2$ 的逆元。$t(x)$ 多项式的初始值为：$t_0(x)=0$，$t_1(x)=1$

即：$A^{-1}(x)=t(x)=t_4(x)=x^2+x+1$

中国剩余定理

在《孙子算经》中有这样一个问题：“今有物不知其数，三三数之剩二（除以3余2），五五数之剩三（除以5余3），七七数之剩二（除以7余2），问物几何？”这个问题称为“孙子问题”，该问题的一般解法国际上称为“中国剩余定理”。

明代程大位在他的著作《直指算法统宗》中，提出了“孙子歌”来求解该问题——“三人同行七十稀，五树梅花廿一枝， 七子团圆正半月，除百令五便得知。”

实际上说的是：只要是除以3余了一个1，就加上一个70；只要是除以5余了一个1，就加上一个21；只要是除以7余了一个1，就加上一个15。然后累加除以105即可。

举例

有一个年级的同学，每 9 人一排多 5 人，每 7 人一排多 1 人，每 5 人一排多 2 人，问这个年级至少有多少人 ？
题中9、7、5三个数两两互质。
则〔7，5〕= 35；〔9，5〕= 45；〔9，7〕= 63；〔9，7，5〕= 315。
为了使 35 被 9 除余 1，用 35×8=280 ；
使 45 被 7 除余 1，用 45×5=225 ；
使 63 被 5 除余 1，用 63×2=126 。
然后，280×5＋225×1＋126×2=1877，
因为，1877>315，所以，1877－315×5=302，就是所求的数。

再加上一句：计算这个总和除以 105 的余数。

分析

问题：计算一个整数 x ，使得它满足除以3余2、除以5余3、除以7余2。

问题分解：

如果能够找到三个整数 $x_1$, $x_2$, $x_3$，使得：

• $x_1$ 除以3余2、除以5余0、除以7余0

• $x_2$ 除以3余0、除以5余3、除以7余0

• $x3$ 除以3余0、除以5余0、除以7余2

那么令 $x=x_1+x_2+x_3$ ，就很容易验证这时的 $x$ 就满足除以3余2、除以5余3、除以7余2。

如果分别称找到整数 $x_1$, $x_2$, $x_3$ 的问题为问题1、问题2、问题3,那么可以看出这三个问题本质上是类似的。

下面对问题1继续分解，如果能够找到一个整数 $y_1$ 满足 $y_1$ 除以3余1、除以5余0、除以7余0，那么令 $x_1=2\times y_1$ ，就很容易验证这时的 $x_1$ 就满足除以3余2、除以5余0、除以7余0。

因此定义

• 问题1-1为：寻找整数 $y_1$ 满足 $y_1$ 除以3余1、除以5余0、除以7余0

• 问题1-2为：寻找整数 $y_2$ 满足 $y_2$ 除以3余0、除以5余1、除以7余0

• 问题1-3为：寻找整数 $y_3$ 满足 $y_3$ 除以3余0、除以5余0、除以7余1

这三个问题本质上是相同的。

如果找到了 $y_1$, $y_2$, $y_3$ ，那么就可以取 $x=2\times y_1+3\times y_2+2\times y_3$ 。

下面以1-1为例：寻找整数 $z$ 使得 $z$ 除以3余1、除以5余0、除以7余0

即满足：$35k\equiv 1(\mathrm{mod}3)$，此时k就是5×7模3的逆，记作$[35^{-1}{]}_3$，那么$z=5\times 7\times [(5\times 7{)}^{-1}{]}_3$

那么我们将问题分解复原可得：

$x=2\times (5\times 7\times [(5\times 7{)}^{-1}{]}_3)+3\times (3\times 7\times [(3\times 7{)}^{-1}{]}_5)+2\times (3\times 5\times [(3\times 5{)}^{-1}{]}_7)$

下面要讨论的是：如果有多个满足要求的整数，那么它们之间有什么关系呢？

假设 $X,Y$ 都满足“除以3余a、除以5余b、除以7余c”。

观察 $X-Y$ 会发现， $X-Y$ 满足“除以3余0、除以5余0、除以7余0”。因此 $X-Y$ 一定是 $3\times 5\times 7=105$ 的倍数。

这也就是说，在“模105同余”的意义下，之前通过分解问题、组合解答的方法所得到的 x 恰恰就是唯一解。

我们不难发现上述问题的解法具有明显的化归思想，将余n的问题全部化归成余1的基础问题，从而解决

一般化描述

下面把这个问题一般化：假设整数 $m_1,m_2,...,m_n$ 是 $k$ 个两两互素的正整数，则对于任意的整数 $a_1,a_2,...,a_n$ ，同余式组

$$\{\begin{array}{rl}x& \equiv a_1(\mathrm{mod}{m}_1)\\ x& \equiv a_2(\mathrm{mod}{m}_2)\\ \dots & \\ x& \equiv a_n(\mathrm{mod}{m}_n)\end{array}$$

一定有解，且解是唯一的，若令$N=\prod _{i=1}^n{m}_i$

则$x\equiv {\sum }_{i=1}^n{a}_i\times \frac{N}{m_i}\times [(\frac{N}{m_i}{)}^{-1}{]}_{m_i}$

特殊情况

$p$ 和 $q$ 是不相同的素数，$n=p\cdot q$ ，则对于任意的一对$(x_1,x_2)$，$0\le x_1<p$ 且 $0\le x_2<q$，存在唯一的数$x$，$0\le x<n$
$x_1=xmodp$ ,且 $x_2=xmodq$ ，所以任意整数 $x$ 都可以使用CRT表示方法唯一的表示成$(x_1,x_2)$。

应用

1.经典问题求解

对于类似的韩信点兵问题，我们就可以使用上述公式，并结合逆元进行求解

2.CRT加速模运算

计算：$2^{1000000}(\mathrm{mod}77)$

一般求法

使用欧拉定理和模重复平方计算法计算，但计算量还是很大：

因为77=7*11，$\phi (77)=\phi (7)\phi (11)=60$

所以$2^{60}\equiv 1(\mathrm{mod}77)$

又1000000=16666*60+40，所以

$2^{1000000}=(2^{60}{)}^{16666}\cdot 2^{40}\equiv 2^{40}(\mathrm{mod}77)$

设m=77，b=2.令a=1.将40写成二进制，$40=2^3+2^5$运用模重复平方法，我们依次计算如下：

• $n_0=0$.计算$a_0=a\equiv 1$，$b_1\equiv b^2\equiv 4(\mathrm{mod}77)$
• $n_1=0$.计算$a_1=a_0\equiv 1$，$b_2\equiv b_1^2\equiv 16(\mathrm{mod}77)$
• $n_2=0$.计算$a_2=a_1\equiv 1$，$b_3\equiv b_2^2\equiv 25(\mathrm{mod}77)$
• $n_3=1$.计算$a_3=a_2{b}_3\equiv 1$，$b_4\equiv b_3^2\equiv 9(\mathrm{mod}77)$
• $n_4=0$.计算$a_4=a_3\equiv 25$，$b_5\equiv b_4^2\equiv 4(\mathrm{mod}77)$
• $n_5=1$.计算$a_5=a_4{b}_5\equiv 23(\mathrm{mod}77)$

最后计算出$2^{1000000}\equiv 23(\mathrm{mod}77)$

使用CRT优化

分析：CRT可以用于大数求模的优化，大致思路是将模数先质因数分解，形成同余式组，然后求出该式中的 $b_1$ 与 $b_2$。

这种我们就彻底将问题转换成了CRT问题

令$x=2^{1000000}$.因为77=7*11，所以$x(\mathrm{mod}77)$等价于求解同余式组

$$\{\begin{array}{rl}x& \equiv b_1(\mathrm{mod}{m}_1)\\ x& \equiv b_2(\mathrm{mod}{m}_2)\end{array}$$

结合欧拉定理：$2^{\phi (7)}\equiv 2^6\equiv 1(\mathrm{mod}7)$

以及1000000=166666*6+4

所以：$b_1=2^{1000000}\equiv (2^6{)}^{166666}\cdot 2^4\equiv 2(\mathrm{mod}7)$

类似的，因为$2^{\phi (11)}\equiv 2^{10}\equiv 1(\mathrm{mod}11)$

以及1000000=10000*10

$b_2=2^{1000000}\equiv (2^{10}{)}^{10000}\equiv 1(\mathrm{mod}11)$

分别求解同余式并结合中国剩余定理有

$x\equiv 2\times (11\times [11^{-1}{]}_7)+1\times (7\times [7^{-1}{]}_{11})\equiv 100\equiv 23(\mathrm{mod}77)$

因此$2^{1000000}\equiv 23(\mathrm{mod}77)$

3.RSA加密优化-CRT表示法中的运算

当我们使用RSA私钥 $(n,d)$ 对密文 $c$ 进行解密(或签名时)，我们需要计算模幂 $m=c^{d}modn$ 。私钥指数 $d$ 并不像公钥指数 $e$ 那样方便。一个 $k$ 比特的模 $n$ ，对应的私钥指数 $d$ 差不多跟它一样长。计算的工作量同长度 $k$ 成正比，所以对于RSA私钥的运算存在优化空间

我们可以使用CRT更有效的计算： $ m=c^d \ mod \ n$，由于模幂的运算量随着模的比特数k的立方增加而增加。所以做两次幂运算mod p和mod q，比做一次幂运算mod n效率要高。

首先使用 $p,q(p>q)$ 提前计算以下值:

• $dP=e^{-1}mod(p-1)$

• $dQ=e^{-1}mod(q-1)$

• $qInv=q^{-1}modp$

然后恢复出 $x$

我们知道$(c^{d}modp,c^{d}modq)$，那么通过CRT我们知道存在唯一的值 $c^{d}modn$ 在范围$[0,n-1]$内。

结合CRT的表示方法$(x_1,x_2)$恢复出 $x$ ，使用Garner’s方程式。

• $x=x_2+h\cdot q$

• $h=((x_1-x_2)(q^{-1}modp))modp$

其中的 $qInv=q^{-1}modp$ 可以提前计算，我们还可以结合欧拉定理来减少$c^{d}modp$ 与 $c^{d}modq$ 指数。

对RSA运算而言

• $dP=e^{-1}mod(p-1)=dmod(p-1)$
• $dQ=e^{-1}mod(q-1)=dmod(p-1)$
• $m_1=c^{dP}(\mathrm{mod}p)$
• $m_2=c^{dQ}(\mathrm{mod}q)$
• $qInv=q^{-1}modp$
• $h=qInv\cdot (m_1-m_2)modp$
• $m=m_2+h\cdot q$

裴蜀定理

描述

裴蜀定理是一个关于最大公约数（或最大公约式）的定理

若 $a,b$ 是整数，且 $gcd(a,b)=d$，那么对于任意的整数 $x,y,ax+by$ 都一定是 $d$ 的倍数，特别地，一定存在整数 $x,y$ ，使$ax+by=d$ 成立。

推论及应用

• $a,b$ 互质的充要条件是存在整数$x，y$ 使 $ax+by=1$.
• 对于裴蜀等式$ax+by=c$，当且仅当 m 是 a 及 b 的最大公约数d的倍数时有整数解。裴蜀等式有解时必然有无穷多个整数解，每组解x,y 都称为裴蜀数，可以拓展欧几里得算法获得。例如：12 和 42 的最大公因數是 6，则方程 $12x+42y=6$ 有解。有$(-3)\times 12+1\times 42=6$，$4\times 12+(-1)\times 42=6$
• 裴蜀等式也可以用来给最大公约数定义：$d$ 其实就是最小的可以写成 $ax+by$ 形式的正整数。

Carmichael定理

在数论中，Carmichael函数的定义为使得 $a^m\equiv 1(\mathrm{mod})n$ 成立的最小正整数 $m$，其中 $(a,n)=1$ ，将 $m$ 记作 $\lambda (n)$ 。在抽象代数术语中，$\lambda (n)$ 是模 $n$ 的乘法群的指数。

Carmichael函数也被称为规约函数(reduced totient function)以及最小泛指数函数(least universal exponent function)。

$\lambda (8)=2$，即 $m=2$ 为使得 $a^m\equiv 1(\mathrm{mod})n$ 成立的最小正整数,此时对于任意的 $a$ 满足$(a,8)=1$ ，有 $a^2=1(\mathrm{mod}8)$ 也就是说$1^2\equiv 1\mathrm{mod}8$，$3^2=9\equiv 1\mathrm{mod}8$，$5^2=25\equiv 1\mathrm{mod}8$，$7^2=49\equiv 1\mathrm{mod}8$

与欧拉函数的关系

对于欧拉函数来说，$\phi (8)=4$，因为欧拉函数只需要满足对于所有与8互素的数 $a$ 有 $a^4\equiv 1(\mathrm{mod}8)$,而不需要满足 $a$ 的最小性。

Carmichael定理

Carmichael定理解释了如何计算素数幂 $p^r$ 的 $\lambda (p^r)$。对于奇数素数的幂以及 2 和 4，$\lambda (p^r)$ 等于欧拉函数 $\phi (p^r)$ ,对于 $2^3$
及以上的 2 的幂次，它等于欧拉函数的一半，即：

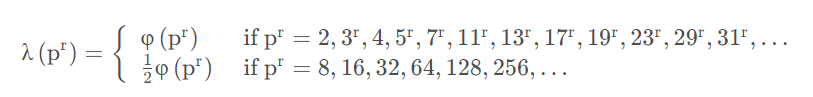
用Carmichael定理计算$\lambda (n)$

根据唯一因式分解定理，任何$n>1$的整数都可以用唯一的方式写成 $n=p_1^{r_1}{p}_2^{r_2}\cdots p_k^{r_k}$,其中，$p_{1}<p_{2}<\ldots<p_{k} $
是由小到大排列的素数, $r_1,r_2,\dots ,r_k$是正整数。那么,$\lambda (n)$就是其中每一项的$\lambda$的最小公倍数，有：

$\lambda (n)=lcm(\lambda (p_1^{r1}),\lambda (p_2^{r2}),\dots ,\lambda (p_k^{rk}))$

上述的公式可由中国剩余定理来证明,这里不再展开。

Carmichael函数的性质

由上述定理易得：

$a|b\Rightarrow \lambda (a)|\lambda (b)$

$\lambda (\mathrm{lcm}(a,b))=\mathrm{lcm}(\lambda (a),\lambda (b))$

二项式定理展开

$(1+x{)}^n={\sum }_{k=0}^n{C}_n^k{x}^k(mod{n}^2)=1+nx(mod{n}^2)$【从$n^2$ 开始后面的项均可以被$n^2$ 整除】

$(1+x{)}^n(mod{n}^2)$的数学处理：

$(1+x{)}^n={\sum }_{k=0}^n{C}_n^k{x}^k(mod{n}^2)=1+nx(mod{n}^2)$

$(1+kn{)}^m\equiv knm+1(\mathrm{mod}{n}^2)$

参考文章：

《深入浅出密码学》

中国剩余定理（CRT ）

使用中国剩余定理CRT对RSA运算进行加速

《信息安全数学基础》-上海交通大学MOOC