文章目录
前言
PPO太经典了,但是我没有完整研究过,补一下。
PG
这类方法都是优化问题,找到参数 θ \theta θ最大化目标函数 J ( θ ) J(\theta) J(θ),大多使用梯度上升的方式。
优点:
- 更好的收敛性质
- 在高维或连续动作空间有效
- 可以学习随机策略
- 不会出现策略退化现象
缺点:
- 可以收敛到不动点,但往往是局部最优
- 对策略的评估往往是低效并且高方差的
- 数据效率和鲁棒性不行。
对于目标函数的推导,这个 和 这个 都写的很好。不过有一个小细节需要注意,大家往往不用 ln x \ln x lnx,而是直接用 log x \log x logx,其中忽略了一些东西, ∂ log x ∂ x = 1 x ln 2 \frac{\partial \log x}{\partial x}=\frac{1}{x\ln 2} ∂x∂logx=xln21,所以需要乘一个 ln 2 \ln2 ln2,其可以作为梯度上升时步长 α \alpha α 的一部分。
PG的目标函数有很多形式,对应不同的算法:

这里 v t v_t vt代表累加奖赏return,更常见的形式是 R t R_t Rt。优势函数有的地方会写成td error,形式是一样的,注意区分。
这里介绍vanilla policy gradient。PG通过计算策略梯度的估计工作,通过梯度上升优化。最常用的梯度估计,也就是基于优势函数的估计:
g ^ = E t ^ [ ∇ θ log π θ ( a t ∣ s t ) A ^ t ] \hat{g}=\hat{E_t}[\nabla_{\theta}\log\pi_{\theta}(a_t|s_t)\hat{A}_t] g^=Et^[∇θlogπθ(at∣st)A^t]
通过对有限batch的样本中求平均估计期望。
我们通过自动微分的软件来做的话,目标函数的梯度就要是这个梯度估计,因此目标函数为:
L P G ( θ ) = E t ^ [ log π θ ( a t ∣ s t ) A ^ t ] L^{PG}(\theta)=\hat{E_t}[\log\pi_{\theta}(a_t|s_t)\hat{A}_t] LPG(θ)=Et^[logπθ(at∣st)A^t]
不能使用相同的轨迹做多步更新,因为会策略相差过大会导致破坏性的大策略更新,导致高方差。这个可以从数学上解释。
重要性采样保证的期望不变:
E x ∼ p [ f ( x ) ] = E x ∼ q [ p ( x ) q ( x ) f ( x ) ] \mathbb{E}_{x\sim p}[f(x)]=\mathbb{E}_{x\sim q}[\frac{p(x)}{q(x)}f(x)] Ex∼p[f(x)]=Ex∼q[q(x)p(x)f(x)]
p ( x ) q ( x ) \frac{p(x)}{q(x)} q(x)p(x)就是新策略与旧策略的比。
但方差不一样,根据 V a r [ x ] = E [ x 2 ] − ( E [ x ] ) 2 Var[x]=\mathbb{E}[x^2]-(\mathbb{E}[x])^2 Var[x]=E[x2]−(E[x])2,可以计算目标分布 p 的方差为:
V a r x ∼ p [ f ( x ) ] = E x ∼ p [ f ( x ) 2 ] − ( E x ∼ p [ f ( x ) ] ) 2 Var_{x\sim p}[f(x)]=\mathbb{E}_{x\sim p}[f(x)^2]-(\mathbb{E}_{x\sim p}[f(x)])^2 Varx∼p[f(x)]=Ex∼p[f(x)2]−(Ex∼p[f(x)])2
根据重要性采样从分布 q 近似 p 的方差为:
V a r x ∼ q [ p ( x ) q ( x ) f ( x ) ] = E x ∼ q [ ( p ( x ) q ( x ) ) 2 f ( x ) 2 ] − ( E x ∼ q [ p ( x ) q ( x ) f ( x ) ] ) 2 = E x ∼ p [ p ( x ) q ( x ) f ( x ) 2 ] − ( E x ∼ p [ f ( x ) ] ) 2 Var_{x\sim q}[\frac{p(x)}{q(x)}f(x)]=\mathbb{E}_{x\sim q}[(\frac{p(x)}{q(x)})^2f(x)^2]-(\mathbb{E}_{x\sim q}[\frac{p(x)}{q(x)}f(x)])^2\\ =\mathbb{E}_{x\sim p}[\frac{p(x)}{q(x)}f(x)^2]-(\mathbb{E}_{x\sim p}[f(x)])^2 Varx∼q[q(x)p(x)f(x)]=Ex∼q[(q(x)p(x))2f(x)2]−(Ex∼q[q(x)p(x)f(x)])2=Ex∼p[q(x)p(x)f(x)2]−(Ex∼p[f(x)])2
因此两者方差是不等的,分布差异影响方差差异。
根据中心极限定理:随着样本容量n的增大(通常要求n≥30),不论原来的总体是否服从正态分布,样本均值的抽样分布都将趋于正态分布,其分布的数学期望为总体均值,方差为总体方差的1/n。
而当采样数据不足够时,方差相差太大会导致两者的样本均值相差很大!
TRPO
TRPO提出了有单调提升保证的迭代优化方法。
令 π \pi π 为随机策略, η ( π ) \eta(\pi) η(π) 为期望累加奖赏,即 η ( π ) = E s 0 , a 0 , ⋯ [ ∑ t = 0 ∞ γ t r ( s t ) ] \eta(\pi)=E_{s_0,a_0,\cdots}[\sum_{t=0}^{\infty}\gamma^t r(s_t)] η(π)=Es0,a0,⋯[∑t=0∞γtr(st)], where s 0 ∼ ρ ( s 0 ) , a t ∼ π ( a t ∣ s t ) , s t + 1 ∼ P ( s t + 1 ∣ s t , a t ) s_0\sim\rho(s_0), a_t\sim\pi(a_t|s_t), s_{t+1}\sim P(s_{t+1}|s_t,a_t) s0∼ρ(s0),at∼π(at∣st),st+1∼P(st+1∣st,at),其中 ρ 0 \rho_0 ρ0 是初始状态 s 0 s_0 s0 的分布。
然后是Q、V、A的定义:
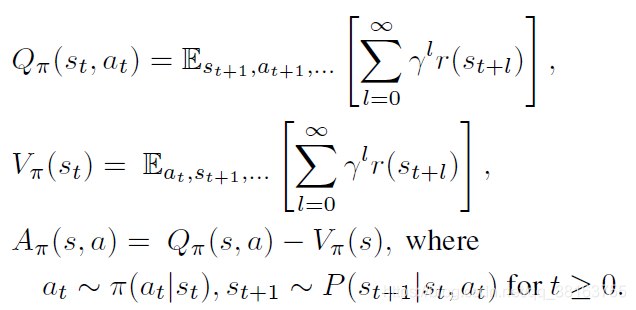
两个策略之间的期望奖赏有如下关系:
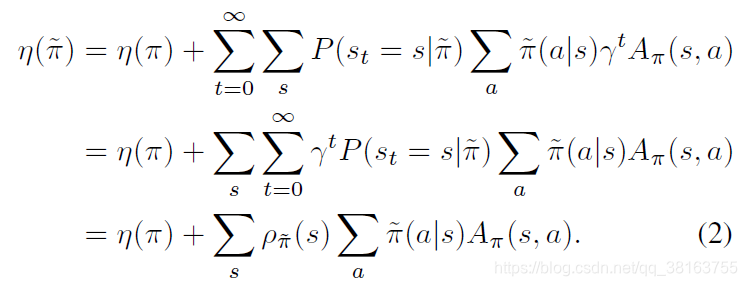
其中 ρ π \rho_{\pi} ρπ 是带折扣的访问频率: ρ π ( s ) = P ( s 0 = s ) + γ P ( s 1 = s ) + γ 2 P ( s 2 = s ) + ⋯ \rho_{\pi}(s)=P(s_0=s)+\gamma P(s_1=s)+\gamma^2 P(s_2=s)+\cdots ρπ(s)=P(s0=s)+γP(s1=s)+γ2P(s2=s)+⋯。
上式说明,如果期望策略改进是有单调性的保证,需要在每个状态都有非负的期望优势 ∑ a π ~ ( a ∣ s ) A π ( s , a ) \sum_a \tilde{\pi}(a|s)A_{\pi}(s,a) ∑aπ~(a∣s)Aπ(s,a),策略迭代的策略改进就满足这一要求。然而在近似设置中,由于估计和近似误差,某个状态的期望优势是负的基本无法避免。 ρ π ~ ( s ) \rho_{\tilde{\pi}}(s) ρπ~(s) 对 π ~ \tilde{\pi} π~ 的复杂依赖使得等式 (2) 很难被直接优化。作者引入了一个局部近似:
L π ( π ~ ) = η ( π ) + ∑ s ρ π ( s ) ∑ a π ~ ( a ∣ s ) A π ( s , a ) L_{\pi}(\tilde{\pi})=\eta(\pi)+\sum_s \rho_{\pi}(s)\sum_a\tilde{\pi}(a|s)A_{\pi}(s,a) Lπ(π~)=η(π)+s∑ρπ(s)a∑π~(a∣s)Aπ(s,a)
其忽略策略改变对状态访问密度的影响,使用 ρ π \rho_{\pi} ρπ,同时忽略了优势函数的近似误差。
对于某一参数化的策略 π θ \pi_{\theta} πθ 来说, L π L_{\pi} Lπ 与 η \eta η 在一阶上匹配:
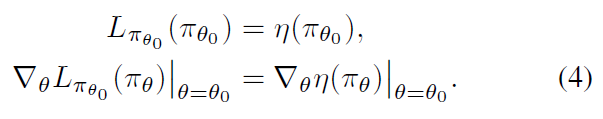
其意味着如果更新步足够小,对 L π L_{\pi} Lπ 的提升也会提升 η \eta η,但是却没说一步应该多大。
保守的策略迭代可以提供一个明确的 η \eta η 更新的下界,相当于软更新: π n e w ( a ∣ s ) = ( 1 − α ) π o l d ( a ∣ s ) + α π ′ ( a ∣ s ) \pi_{new}(a|s)=(1-\alpha)\pi_{old}(a|s)+\alpha \pi'(a|s) πnew(a∣s)=(1−α)πold(a∣s)+απ′(a∣s),其中 π ′ = arg max π ′ L π o l d ( π ′ ) \pi'=\arg\max_{\pi'}L_{\pi_{old}}(\pi') π′=argmaxπ′Lπold(π′),下界为:

但是请注意,到目前为止,此界限仅适用于由保守地策略更新生成的混合策略。这个策略类在实践中是笨拙和限制性的,希望有一个适用于所有一般随机策略类的实用策略更新方案。
作者的主要理论就是上式的bound可以被扩展到一半随机策略,而不只是混合策略,因为其在实际中很少用到。作者使用 total variation divergence 作为距离度量,即 D T V ( p ∣ ∣ q ) = 1 2 ∑ i ∣ p i − q i ∣ D_{TV}(p||q)=\frac{1}{2}\sum_i|p_i-q_i| DTV(p∣∣q)=21∑i∣pi−qi∣, p , q p,q p,q是离散概率分布。
定义 D T V m a x ( π , π ~ ) = max s D T V ( π ( ⋅ ∣ s ) ∣ ∣ π ~ ( ⋅ ∣ s ) ) D_{TV}^{max}(\pi,\tilde{\pi})=\max_s D_{TV}(\pi(\cdot|s)||\tilde{\pi}(\cdot|s)) DTVmax(π,π~)=maxsDTV(π(⋅∣s)∣∣π~(⋅∣s)),作者提出一个理论扩展上面的下界:
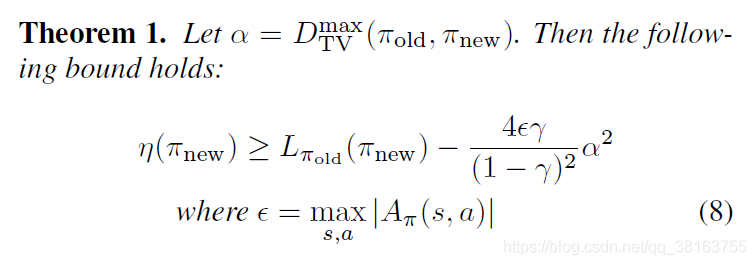
然后是 total variation divergence 与 KL 散度之间有这样的关系: D T V ( p ∣ ∣ q ) 2 ≤ D K L ( p ∣ ∣ q ) D_{TV}(p||q)^2\le D_{KL}(p||q) DTV(p∣∣q)2≤DKL(p∣∣q),令 D K L m a x ( π , π ~ ) = max s D K L ( π ( ⋅ ∣ s ) ∣ ∣ π ~ ( ⋅ ∣ s ) ) D_{KL}^{max}(\pi,\tilde{\pi})=\max_s D_{KL}(\pi(\cdot|s)||\tilde{\pi}(\cdot|s)) DKLmax(π,π~)=maxsDKL(π(⋅∣s)∣∣π~(⋅∣s)),可得新的下界:
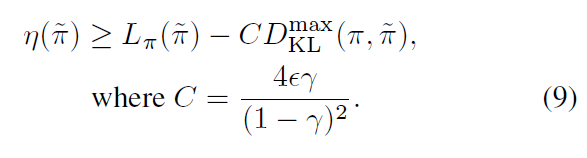
下面这个算法就保证了策略的单调提升

这是个最小-最大算法,TRPO是它的一个近似,通过约束而不是惩罚,因为大的惩罚系数会导致过于小的step,但又很难鲁棒地选择系数。
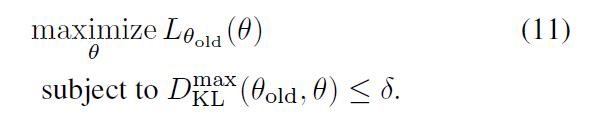
但由于 D K L m a x D_{KL}^{max} DKLmax对于数值优化和估计困难,因此作者使用平均的 KL-散度,也就是 max 变成了期望:
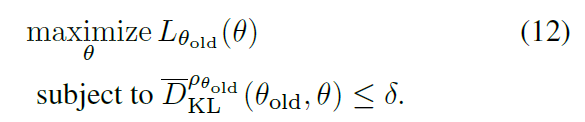
作者通过实验说明这种跟max约束的性能相似。
令 q q q 为采样分布,则可通过重要性采样近似:
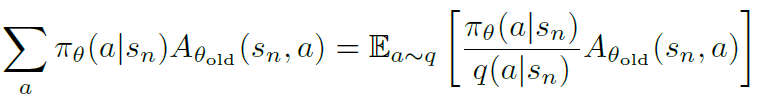
这个期望通过采样平均的方式估计。
综上,目标函数变成了带约束的优化问题,约束项限制了策略更新的幅度:

在对目标进行线性逼近和对约束进行二次逼近之后,可以使用共轭梯度算法有效地近似解决这个问题。
简单来说,证明 TRPO 合理的理论实际上表明使用惩罚而不是约束,即解决无约束优化问题:

这是因为某个surrogate目标(计算状态的最大 KL 而不是平均值)形成了策略性能的下限(即悲观界限)。TRPO 使用硬约束而不是惩罚,因为很难选择一个值 β \beta β 在不同问题中表现良好——甚至在单个问题中,特征在学习过程中发生变化。
此外其比较复杂,并且不适用于包含噪声(dropout)或参数共享(策略与值函数,或与辅助任务)。
PPO
为了实现模拟 TRPO 单调提升的一阶算法的目标,实验表明,简单地选择一个固定的惩罚系数 β \beta β 并使用 SGD 优化惩罚目标方程是不够的;需要额外的修改,也就产生了PPO,其中包括两种目标函数。
令概率ratio为 r t = π θ ( a t ∣ s t ) π θ o l d ( a t ∣ s t ) r_t = \frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)} rt=πθold(at∣st)πθ(at∣st),
Clipped Surrogate Objective
conservative policy iteration目标如下:
L C P I ( θ ) = E ^ t [ r t ( θ ) A ^ t ] L^{CPI}(\theta)=\hat{\mathbb{E}}_t[r_t(\theta)\hat{A}_t] LCPI(θ)=E^t[rt(θ)A^t]
最大化这个目标会导致极大的策略更新,进而导致大方差,PPO考虑如何惩罚大更新。
L C L I P ( θ ) = E ^ t [ min ( r t ( θ ) A ^ t , c l i p ( r t ( θ ) , 1 − ϵ , 1 + ϵ ) A ^ t ) ] L^{CLIP}(\theta)=\hat{\mathbb{E}}_t[\min(r_t(\theta)\hat{A}_t,clip(r_t(\theta),1-\epsilon,1+\epsilon)\hat{A}_t)] LCLIP(θ)=E^t[min(rt(θ)A^t,clip(rt(θ),1−ϵ,1+ϵ)A^t)]
其中 ϵ = 0.2 \epsilon=0.2 ϵ=0.2,当 A ^ t > 0 \hat{A}_t>0 A^t>0,使用 1 + ϵ 1+\epsilon 1+ϵ,反之 1 − ϵ 1-\epsilon 1−ϵ,对应两种场景下 r t r_t rt 的变化,不过都是设置天花板。min 使得该目标是一个下界,同时当 ratio 的改变提升目标时我们忽略,但不忽略对目标的降低。
Adaptive KL Penalty Coefficient
这里使用KL-散度,同时系数自适应来实现KL-散度的目标值 d t a r g d_{targ} dtarg,不过实验不如 CLIP。
每次策略更新包含两步,一是优化目标:
L K L P E N ( θ ) = E ^ t [ r t ( θ ) A ^ t − β K L [ π θ o l d ( ⋅ ∣ s t ) ∣ ∣ π θ ( ⋅ ∣ s t ) ] ] L^{KLPEN}(\theta)=\hat{\mathbb{E}}_t[r_t(\theta)\hat{A}_t-\beta KL[\pi_{\theta_{old}}(\cdot|s_t)||\pi_{\theta}(\cdot|s_t)]] LKLPEN(θ)=E^t[rt(θ)A^t−βKL[πθold(⋅∣st)∣∣πθ(⋅∣st)]]
然后计算 d = E ^ t [ K L [ π θ o l d ( ⋅ ∣ s t ) ∣ ∣ π θ ( ⋅ ∣ s t ) ] ] d=\hat{\mathbb{E}}_t[KL[\pi_{\theta_{old}}(\cdot|s_t)||\pi_{\theta}(\cdot|s_t)]] d=E^t[KL[πθold(⋅∣st)∣∣πθ(⋅∣st)]],如果 d < d t a r g 1.5 , β = β 2 d<\frac{d_{targ}}{1.5}, \beta=\frac{\beta}{2} d<1.5dtarg,β=2β,如果 d > d t a r g × 1.5 , β = β × 2 d>d_{targ} \times1.5, \beta=\beta\times 2 d>dtarg×1.5,β=β×2。这两个值和 β \beta β 初始值都不重要,因为会很快调整,不敏感。
如果策略和值函数 VF 共享神经网络参数,则使用结合的目标,并增加熵确保足够的探索,即最大化:
L t C L I P ( θ ) − c 1 L t V F ( θ ) + c 2 S [ π θ ] ( s t ) L^{CLIP}_t(\theta)-c_1 L_t^{VF}(\theta)+c_2S[\pi_{\theta}](s_t) LtCLIP(θ)−c1LtVF(θ)+c2S[πθ](st)
收集一定长度的样本,然后计算优势函数:
A ^ t = ∑ i = t T − 1 γ i − t r i + γ T − t V ( s T ) − V ( s t ) \hat{A}_t=\sum_{i=t}^{T-1}\gamma^{i-t}r_i+\gamma^{T-t}V(s_T)-V(s_t) A^t=i=t∑T−1γi−tri+γT−tV(sT)−V(st)
同时可以得到 GAE:
A ^ t = δ t + ( γ λ ) δ t + 1 + ⋯ + ( γ λ ) T − t + 1 δ T − 1 \hat{A}_t=\delta_t+(\gamma\lambda)\delta_{t+1}+\cdots+(\gamma\lambda)^{T-t+1}\delta_{T-1} A^t=δt+(γλ)δt+1+⋯+(γλ)T−t+1δT−1
δ T = r t + γ V ( s t + 1 ) − V ( s t ) \delta_T=r_t+\gamma V(s_{t+1})-V(s_t) δT=rt+γV(st+1)−V(st)
下面的伪代码是多个actor并行的形式,收集 NT 数据后进行 K epochs 的训练:

TRPO 和 PPO 是 on-policy吗
都是 on-policy。
TRPO 的重要性采样源于近似,其原本的优化目标是:

但是一条样本中很难获取所有动作的advantage,这里使用重要性采样的期望近似动作概率与优势函数的加权和,
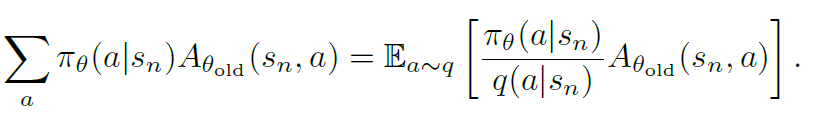
期望通过样本平均来近似,所以方法本身是on-policy,只是为了实用性做了一些近似。
PPO 方法上是on-policy,技术上使用同一个样本多次是不对的,但是不用的话会不稳定。下面是 OpenAI 研究员 Matthias Plappert 的说法:
PPO is an on-policy algorithm so you are correct that going over the same data multiple times is technically incorrect.
However, we found that PPO is actually quite okay with doing this and we still get stable convergence. This is likely due to the proximal trust region constrained that we enforce, which means that the policy cannot change that much anyway when going over the current set of transitions multiple times, making it still approximately on-policy. You can of course get rid of this but then you’ll need more samples.
IMPALA
IMPALA是一种高吞吐量的方法,也是后来大规模分布式框架采用的模式,就是actor-learner的结构,多个actor并行生成经验,而learner使用所有生成的经验优化策略和价值函数参数。actor定期使用learner的最新策略更新他们的参数。因为acting和learning是解耦的,我们可以使用更多actor,以在每个时间单位生成更多的轨迹。由于目标策略和行为策略不完全同步,它们之间存在差距,因此我们需要进行off-policy修正,即V-trace。
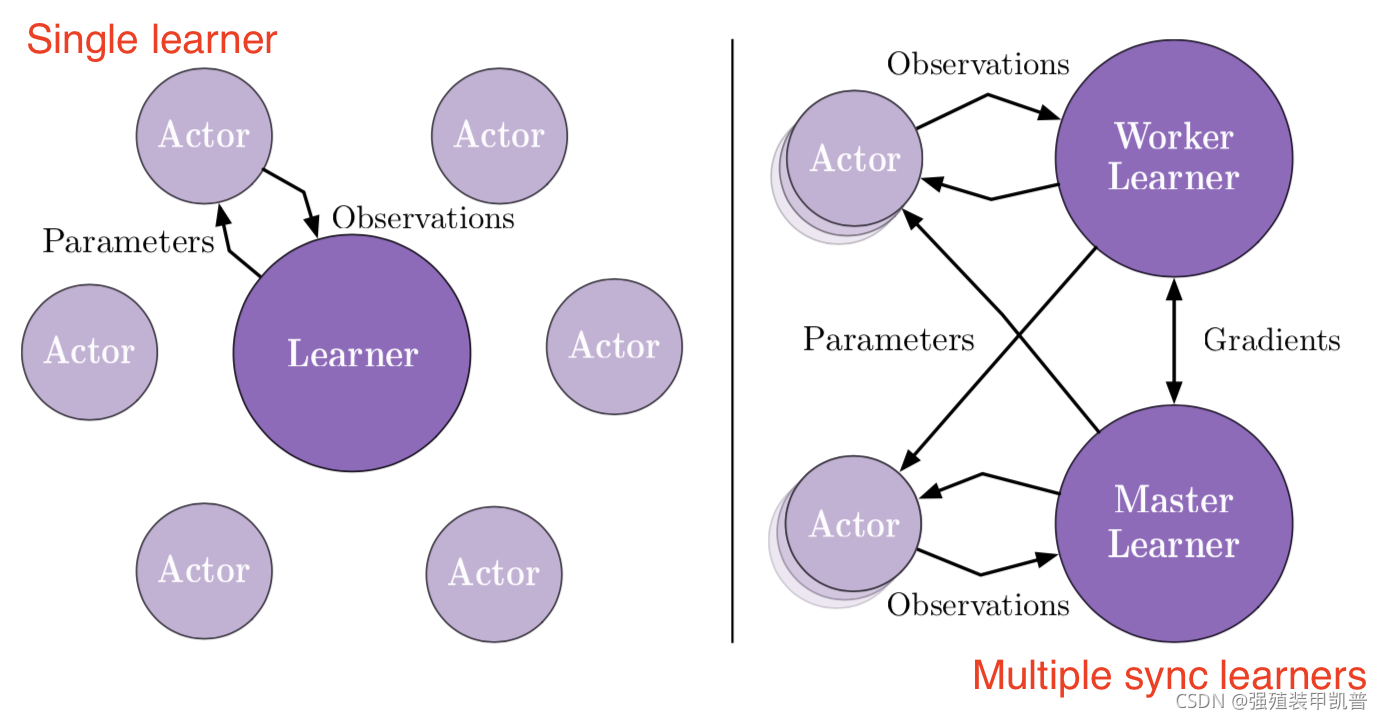
A3C与其有很多相似之处,
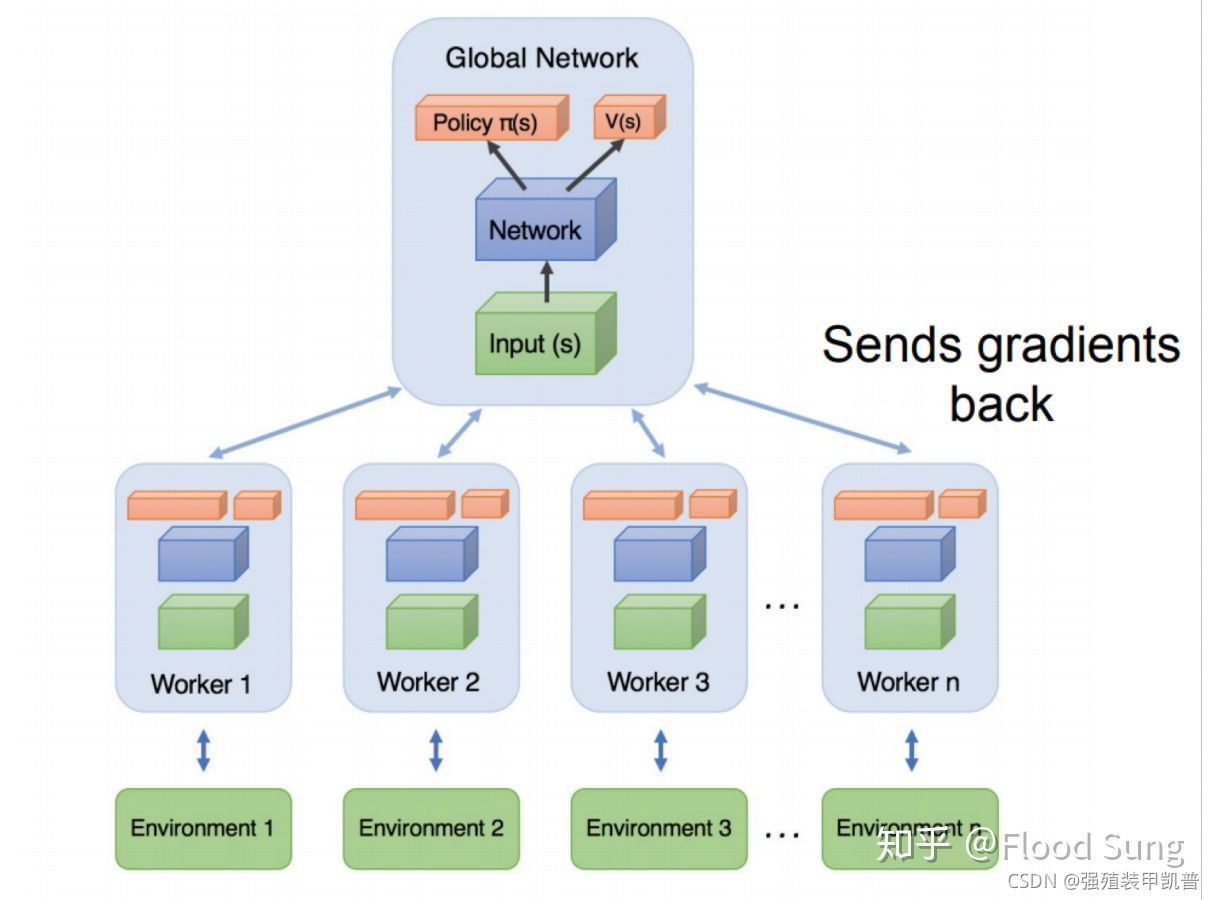
A3C 是最早出现的版本,采用异步梯度更新的方式,不同的 worker 获取独立的经验后(一个 batch),独立的去更新 Global Network,当主网络参数被更新了以后,就用最新的参数去重置所有的 worker,然后在开始下一轮循环。但是其他正在运行的worker需要跑完当前episode之后才更新,所以策略就存在了不同步。主网络保持着最新的策略,各 worker 跟主网络同步的时间也是不一样的,只要有一个 worker 完成当前episode,主网络就会根据它的梯度进行更新,并不影响其它仍旧在使用旧策略的 worker。这就是异步并行的核心思想。由于传递的是梯度,导致只能在CPU上训练,没有GPU快。
然后就有了同步更新的A2C。
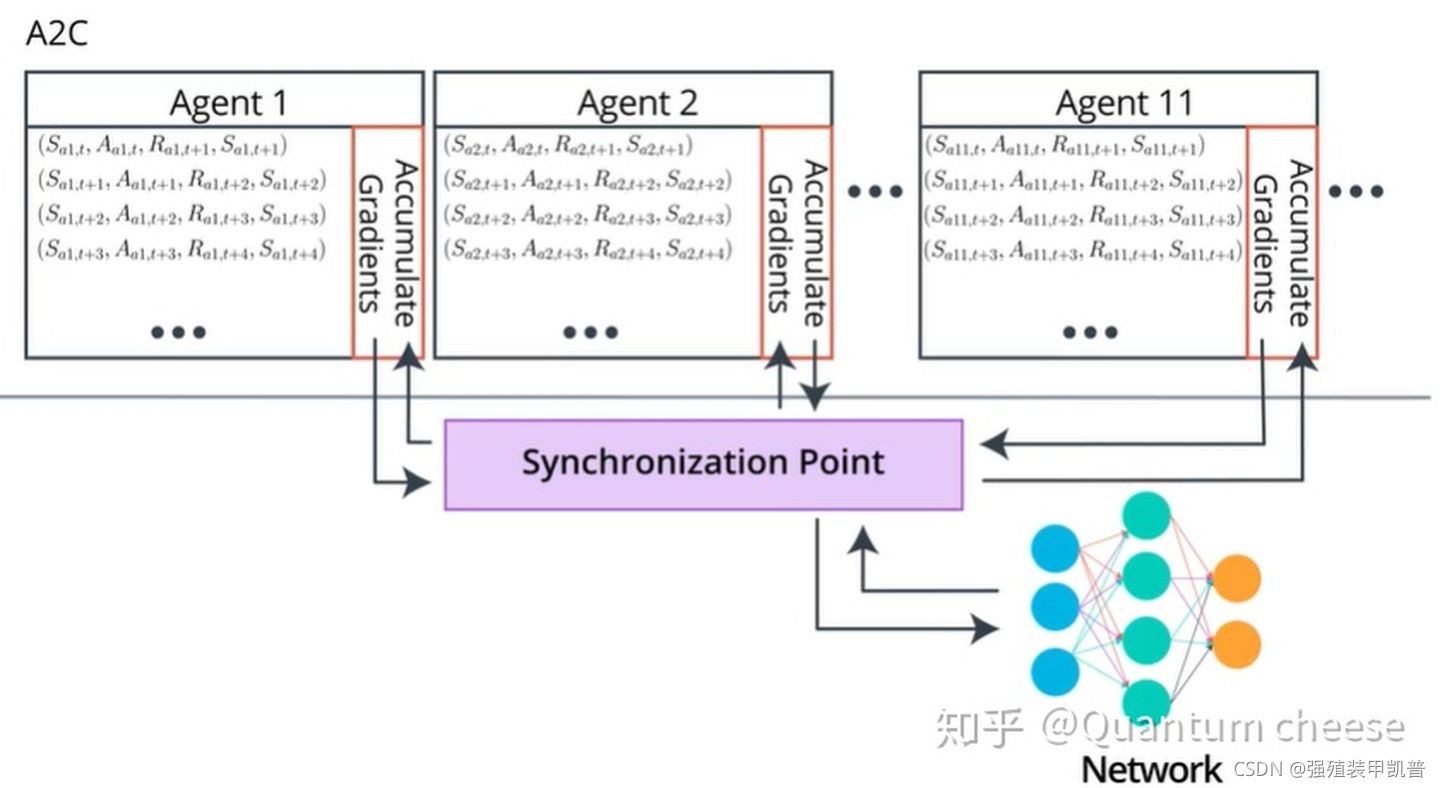
每轮训练中,Global network 都会等待每个 worker 各自完成当前的 episode,然后把这些 worker 上传的梯度进行汇总并求平均,得到一个统一的梯度并用其更新主网络的参数,最后用这个参数同时更新所有的 worker。 相当于在 A3C 基础上加入了一个同步的环节。
A2C 跟 A3C 的一个显著区别就是,在任何时刻,不同 worker 使用的其实是同一套策略,它们是完全同步的,更新的时机也是同步的。由于各 worker彼此相同,其实 A2C 就相当于只有两个网络,其中一个 Global network 负责参数更新,另一个负责跟环境交互收集经验,只不过它利用了并行的多个环境,可以收集到去耦合的多组独立经验。
每一个worker仅采集数据,然后集中起来通过GPU进行更新,这样会快很多。也基本上,接下来的架构都不传梯度了,只传数据。
IMPALA可以看做是A2C的进阶版,A2C的问题是每一个Actor(worker)都需要采样完毕了才能输送给Learner进行训练,那么IMPALA通过importance sampling的做法来使得Actor和Learner可以相对独立,两者的网络不用完全一样也可以更新,只要数据采集够了,就可以送到learner进行训练,这样速度会快很多。

其是压缩算子,可以计算得到V-trace的不动点为:
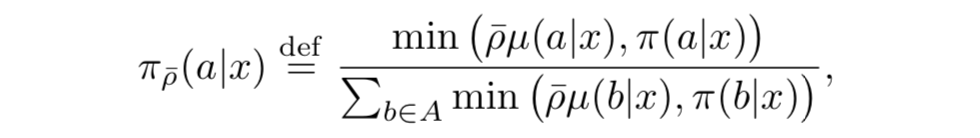
所以当 ρ ˉ < ∞ \bar{\rho}<\infin ρˉ<∞时,不动点介于目标策略和行为策略之间,当 ρ ˉ = ∞ \bar{\rho}=\infin ρˉ=∞时,不动点为目标策略, ρ ˉ \bar{\rho} ρˉ接近0时,我们估计的是行为策略的值函数。
c ˉ \bar{c} cˉ类似于"trace cutting"系数,乘积度量着在时间 i 观察到的时间差分 δ i V \delta_i V δiV 对前一时间 t 的价值函数更新有多大影响。目标策略和行为策略相差越大,这个乘积的方差越大,这里通过截断来限制方差。
总的来说: ρ ˉ \bar{\rho} ρˉ影响收敛到的价值函数估计的是哪个策略, c ˉ \bar{c} cˉ影响收敛到这个函数的速度。