Content
小波变换系列
小波变换第1讲:Why wavelet?
小波变换第2讲:尺度函数与小波函数
前文小波变换第1讲:Why wavelet?介绍了FT以及STFT在时频分析方面的缺陷,本文将介绍小波变换的主体部分。
小波变换(WT)方面的不同书籍,涉及到的一些定义不尽相同,对理解小波造成了一些困扰。本文主要参考的是冈萨雷斯 数字图像处理 第3版第7章的有关内容。
本文中的尺度函数选取Haar函数。
1 尺度函数
尺度函数(scaling function),通常记作 ϕ ( t ) \phi(t) ϕ(t),又称为father wavelet。
1.1 Harr尺度函数
Harr尺度函数及图示如下:
ϕ ( t ) = { 1 , 0 ≤ t < 1 0 , o t h e r w i s e \phi_(t)=\left\{ \begin{aligned} 1&,0\le t<1 \\ 0&, otherwise \end{aligned} \right. ϕ(t)={
10,0≤t<1,otherwise
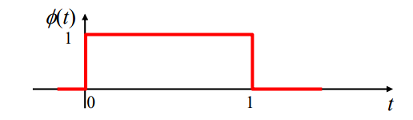
对该函数进行缩放或平移:
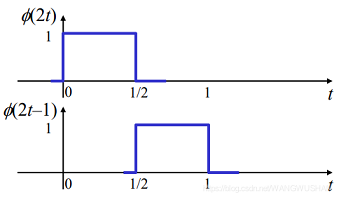
该函数在不同的尺度 j , k ( j = 0 , ± 1 , ± 2 , . . . ; k = 0 , ± 1 , ± 2 , . . . ) j,k(j=0,\pm1,\pm2,...;k=0,\pm1,\pm2,...) j,k(j=0,±1,±2,...;k=0,±1,±2,...)缩放( 2 j 2^j 2j)及平移( 2 − j k 2^{-j}k 2−jk),形成了一个集合 { ϕ j , k ( t ) } \{\phi_{j,k}(t)\} {
ϕj,k(t)}:
ϕ j , k ( t ) = 2 j 2 ϕ ( 2 j t − k ) \phi_{j,k}(t)=2^{\frac{j}{2}}\phi(2^jt-k) ϕj,k(t)=22jϕ(2jt−k)
这里 j 2 \cfrac{j}{2} 2j的作用是为了保持 ∫ a b ∣ f ( t ) ∣ 2 d t \int_a^b|f(t)|^2dt ∫ab∣f(t)∣2dt不变,即能量不变。
1.2 尺度函数构成的空间
尺度函数形成的子空间应该来说是小波变换中一个非常重要的性质。

设空间 V j V_j Vj是由 ϕ j , k ( t ) , k = 0 , ± 1 , ± 2 , . . . \phi_{j,k}(t),k=0,\pm1,\pm2,... ϕj,k(t),k=0,±1,±2,...在实数域内张成的空间,即:
V j V_j Vj空间中的任一函数 f ( t ) f(t) f(t)可表示为:
f ( t ) = ∑ k ∈ Z a k ϕ j , k ( t ) f(t)=\sum\limits_{k\in Z}a_k\phi_{j,k}(t) f(t)=k∈Z∑akϕj,k(t)
1.3 尺度函数的性质
1.3.1 V j V_j Vj空间的正交基
对于 V j V_j Vj空间的任一基函数,均满足:
⟨ ϕ j , m ( t ) , ϕ j , n ( t ) ⟩ = { 0 , m ! = n 1 , m = n \langle\phi_{j,m}(t),\phi_{j,n}(t)\rangle= \left\{ \begin{aligned} 0&,m!=n \\ 1&, m=n \end{aligned} \right. ⟨ϕj,m(t),ϕj,n(t)⟩={
01,m!=n,m=n
可以看下1.1节Harr函数 ϕ ( 2 t ) \phi(2t) ϕ(2t)与 ϕ ( 2 t − 1 ) \phi(2t-1) ϕ(2t−1),即 ϕ 1 , 0 ( t ) \phi_{1,0}(t) ϕ1,0(t)、 ϕ 1 , 1 ( t ) \phi_{1,1}(t) ϕ1,1(t),二者积分为0,正交。
1.3.2 嵌套子空间
子空间在小波变换中非常重要。1.3.1正交基是定义在相同的尺度 j j j,而本小节子空间是定义在不同的尺度 j j j。
不同尺度j形成的空间之间的关系如图所示:
V − ∞ ⊂ ⋯ ⊂ V − 1 ⊂ V 0 ⊂ V 1 ⊂ V 2 ⊂ ⋯ ⊂ V ∞ V_{-\infin} \subset \cdots \subset V_{-1} \subset V_{0} \subset V_{1} \subset V_{2} \subset \cdots \subset V_{\infin} V−∞⊂⋯⊂V−1⊂V0⊂V1⊂V2⊂⋯⊂V∞
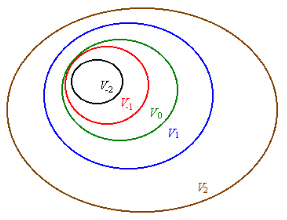
举例说明, V 0 V_0 V0是 V 1 V_1 V1的一个子空间,即 V 0 ⊂ V 1 V_0 \subset V_1 V0⊂V1,则 V 0 V_0 V0中的任一函数可由 V 1 V_1 V1中的基线性表示:
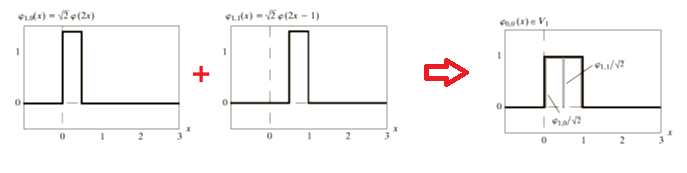
这样,对于任一函数 f ( t ) f(t) f(t),总能用尺度趋向于无限大的空间 V ∞ V_\infty V∞中的基函数线性表示,即若 f ( t ) ∈ V j f(t) \in V_j f(t)∈Vj,
又因为 V j ⊂ V ∞ V_j \subset V_\infty Vj⊂V∞,则 f ( t ) f(t) f(t)也必然 ∈ V ∞ \in V_\infty ∈V∞。
当然,我们不可能用 V ∞ V_\infty V∞中的基函数表示,这涉及到效率和资源的问题。
有点类似AD转换中的逐次逼近法,先确定最高位,然后除2,不断确定次低位~
1.3.3 交空间和并空间
由1.2.2节嵌套子空间,可以得到下列性质:
- 交空间
⋂ j V j = V − ∞ = { 0 } \bigcap_jV_j=V_{-\infin}=\{0\} j⋂Vj=V−∞={ 0} - 并空间
⋃ j V j = V ∞ = { L 2 ( R ) } \bigcup_jV_j=V_{\infin}=\{L^2(R)\} j⋃Vj=V∞={ L2(R)}
L 2 ( R ) : L^2(R): L2(R):平方可积函数空间,是指函数 f ( x ) ∈ R f(x)\in R f(x)∈R,且 ∣ f ( x ) ∣ 2 |f(x)|^2 ∣f(x)∣2在 R R R内可积,这样的函数构成的集合。
1.3.4 尺度函数递归等式
由1.3.2节, V j ⊂ V j + 1 V_{j} \subset V_{j+1} Vj⊂Vj+1,则:
ϕ j , k ( t ) = ∑ n a n ⋅ ϕ j + 1 , n ( t ) \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\phi_{j,k}(t)=\sum_na_n\cdot\phi_{j+1,n}(t) ϕj,k(t)=∑nan⋅ϕj+1,n(t)
又根据1.1节,
ϕ j , k ( t ) = 2 j 2 ϕ ( 2 j t − k ) ϕ j + 1 , n ( t ) = 2 j + 1 2 ϕ ( 2 j + 1 t − n ) \phi_{j,k}(t)=2^{\frac{j}{2}}\phi(2^jt-k)\\ \phi_{j+1,n}(t)=2^{\frac{j+1}{2}}\phi(2^{j+1}t-n) ϕj,k(t)=22jϕ(2jt−k)ϕj+1,n(t)=22j+1ϕ(2j+1t−n)
令 j = 0 , k = 0 j=0,k=0 j=0,k=0,并用 h ϕ ( n ) h_{\phi}{(n)} hϕ(n)替代 a n a_n an,有:
ϕ ( t ) = ∑ n h ϕ ( n ) 2 ϕ ( 2 t − n ) \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\phi(t)=\sum_nh_{\phi}{(n)}\sqrt{2}\phi(2t-n) ϕ(t)=∑nhϕ(n)2ϕ(2t−n)
对于Haar小波尺度函数之间存在如下关系,详见下图:
ϕ ( t ) = 2 [ 1 2 ϕ ( 2 t ) + 1 2 ϕ ( 2 t − 1 ) ] \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\phi(t)=\sqrt{2}\lbrack\cfrac{1}{\sqrt2}\phi(2t)+\cfrac{1}{\sqrt2}\phi(2t-1)\rbrack ϕ(t)=2[21ϕ(2t)+21ϕ(2t−1)]
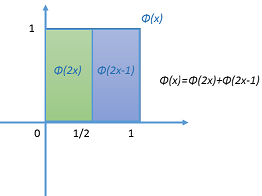
哈工大冉启文老师《小波变换与分数傅里叶变换理论及应用》将上述关系归纳为:
- 嵌套关系/单调性: V j ⊂ V j + 1 V_{j} \subset V_{j+1} Vj⊂Vj+1
- 唯一关系: ⋂ j V j = { 0 } \bigcap_jV_j=\{0\} ⋂jVj={ 0}
- 稠密关系: ⋃ j V j = { L 2 ( R ) } \bigcup_jV_j=\{L^2(R)\} ⋃jVj={ L2(R)}
- 伸缩关系: f ( x ) ∈ V j , 则 f ( 2 x ) ∈ V j + 1 f(x)\in V_j,则f(2x)\in V_{j+1} f(x)∈Vj,则f(2x)∈Vj+1
2 小波函数
小波函数(wavelet function),通常记作 ψ ( t ) \psi(t) ψ(t),又称为mother wavelet。
小波函数与尺度函数有联系也有区别。
2.1 Harr小波函数
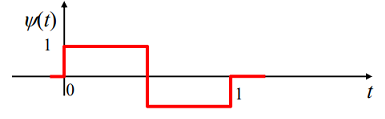
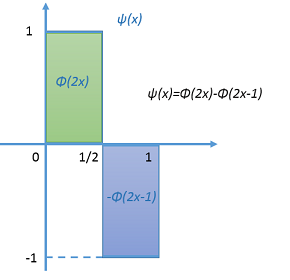
Harr小波函数及图示如下:
ψ ( t ) = { 1 0 ≤ t < 1 2 , − 1 1 2 ≤ t < 1 , 0 o t h e r w i s e . \psi_(t)=\left\{ \begin{aligned} 1&\qquad0\le t<\cfrac{1}{2}, \\ -1&\qquad\cfrac{1}{2}\le t<1, \\ 0&\qquad\ otherwise. \end{aligned} \right. ψ(t)=⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧1−100≤t<21,21≤t<1, otherwise.
类似于尺度函数,小波函数在不同的尺度 j , k ( j = 0 , ± 1 , ± 2 , . . . ; k = 0 , ± 1 , ± 2 , . . . ) j,k(j=0,\pm1,\pm2,...;k=0,\pm1,\pm2,...) j,k(j=0,±1,±2,...;k=0,±1,±2,...)缩放( 2 j 2^j 2j)及平移( 2 − j k 2^{-j}k 2−jk),形成了一个集合 { ψ j , k ( t ) } \{\psi_{j,k}(t)\} {
ψj,k(t)}:
ψ j , k ( t ) = 2 j 2 ψ ( 2 j t − k ) \psi_{j,k}(t)=2^{\frac{j}{2}}\psi(2^jt-k) ψj,k(t)=22jψ(2jt−k)
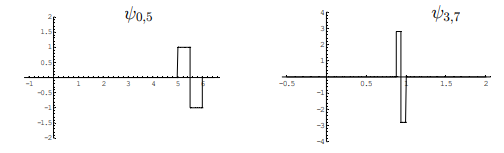
小波函数也可以进行缩放和平移:
2.2 小波函数构成的空间
设空间 W j W_j Wj是由 ψ j , k ( t ) , k = 0 , ± 1 , ± 2 , . . . \psi_{j,k}(t),k=0,\pm1,\pm2,... ψj,k(t),k=0,±1,±2,...在实数域内张成的空间,即:
W j W_j Wj空间中的任一函数 g ( t ) g(t) g(t)可表示为:
g ( t ) = ∑ k ∈ Z b k ψ j , k ( t ) g(t)=\sum\limits_{k\in Z}b_k\psi_{j,k}(t) g(t)=k∈Z∑bkψj,k(t)
2.3 小波函数的性质
2.3.1 小波函数子空间之间的正交性
尺度函数子空间只针对同一尺度 j j j、不同的平移系数 k k k成立。
而小波函数子空间的正交性,则是针对所有尺度 j j j(相同或不相同)、及不同平移系数 k k k的小波函数。即:
⟨ ψ j , k ( t ) , ψ j ′ , k ′ ( t ) ⟩ = 0 , 当 { j = j ′ , k ≠ k ′ j ≠ j ′ \qquad\qquad\qquad\langle\psi_{j,k}(t),\psi_{j',k'}(t)\rangle=0 ,当\left\{ \begin{aligned} & j=j',k \neq k' \\ & j\ne j' \end{aligned} \right. ⟨ψj,k(t),ψj′,k′(t)⟩=0,当{
j=j′,k=k′j=j′
下图展示了 ψ 1 , 0 ( t ) \psi_{1,0}(t) ψ1,0(t),与 ψ 0 , 0 ( t ) \psi_{0,0}(t) ψ0,0(t)即 ψ ( t ) \psi(t) ψ(t)的正交关系。
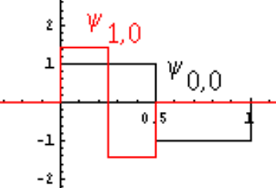
2.3.2 小波函数与尺度函数空间的关系
2.3.2.1 正交补空间
尺度函数子空间 V j V_j Vj、小波函数子空间 W j W_j Wj与尺度函数 V j + 1 V_{j+1} Vj+1满足:
V j + 1 = V j ⊕ W j \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad V_{j+1}=V_{j}\oplus W_{j} Vj+1=Vj⊕Wj
V j V_j Vj、 W j W_j Wj空间正交,即:
⟨ ϕ j , k ( t ) , ψ j , l ( t ) ⟩ = 0 \qquad\qquad\qquad\langle\phi_{j,k}(t),\psi_{j,l}(t)\rangle=0 ⟨ϕj,k(t),ψj,l(t)⟩=0,对所有 j , k , l j,k,l j,k,l均成立。
2.3.2.2 子空间之间的关系
由于小波函数子空间及尺度函数子空间之间存在的正交关系,尺度函数空间 V j V_j Vj,可由起始尺度空间如 V 0 V_0 V0,与一系列低尺度的小波函数空间 W j − 1 , W j − 2 , . . . , W 1 , W 0 W_{j-1},W_{j-2},...,W_1,W_0 Wj−1,Wj−2,...,W1,W0的合成:
V 2 = V 1 ⊕ W 1 = V 0 ⊕ W 0 ⊕ W 1 \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad V_2=V_1\oplus W_1=V_0 \oplus W_0\oplus W_1 V2=V1⊕W1=V0⊕W0⊕W1

推广之,
V n = V n − 1 ⊕ W n − 1 = V n − 2 ⊕ W n − 2 ⊕ W n − 1 = V 0 ⊕ W 0 ⊕ W 1 ⊕ . . . ⊕ W n − 1 = V − ∞ ⊕ W − ∞ ⊕ . . . ⊕ W − 1 ⊕ W 0 ⊕ W 1 ⊕ . . . ⊕ W n − 1 \begin{aligned} V_n&=V_{n-1}\oplus W_{n-1}\\&=V_{n-2} \oplus W_{n-2}\oplus W_{n-1}\\ &=V_0 \oplus W_{0}\oplus W_{1}\oplus ... \oplus W_{n-1}\\ &=V_{-\infin} \oplus W_{-\infin} \oplus ...\oplus W_{-1}\oplus W_{0}\oplus W_{1}\oplus ... \oplus W_{n-1} \end{aligned} Vn=Vn−1⊕Wn−1=Vn−2⊕Wn−2⊕Wn−1=V0⊕W0⊕W1⊕...⊕Wn−1=V−∞⊕W−∞⊕...⊕W−1⊕W0⊕W1⊕...⊕Wn−1
当然我们不可能从 − ∞ -\infin −∞尺度开始,而往往选择从尺度为0的分辨率开始。
又由1.3.3节, V − ∞ = { 0 } V_{-\infin}=\{0\} V−∞={
0},因此:
V n = ⨁ j = − ∞ n − 1 W k \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad V_n=\bigoplus \limits_{j=-\infin}^{n-1}W_k Vn=j=−∞⨁n−1Wk
当 n → ∞ n\rightarrow \infin n→∞时,由1.3.3节并空间的性质, V ∞ = { L 2 ( R ) } V_{\infin}=\{L^2(R)\} V∞={ L2(R)},故对于任意 f ( x ) ∈ L 2 ( R ) f(x)\in L^2(R) f(x)∈L2(R),均有:
f ( x ) = v 0 + ∑ j = 0 ∞ w j \qquad\qquad\qquad\qquad\qquad\qquad f(x)=v_0+\sum\limits_{j=0}^{\infin}w_j f(x)=v0+j=0∑∞wj,其中 v 0 ∈ V 0 v_0\in V_0 v0∈V0, w j ∈ W j w_j\in W_j wj∈Wj。
L 2 ( R ) {L^2(R)} L2(R)中的任意函数均可由小波正交空间中的函数线性表示。
2.3.3 小波函数递归等式
由 V j + 1 = V j ⊕ W j V_{j+1}=V_{j}\oplus W_{j} Vj+1=Vj⊕Wj,则 W j W_{j} Wj和 V j V_{j} Vj都是 V j + 1 V_{j+1} Vj+1的子空间。因此与1.3.4类似,小波函数也可由相邻的较高分辨率的尺度函数来线性表示:
ψ ( t ) = ∑ n h ψ ( n ) 2 ϕ ( 2 t − n ) \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \psi(t)=\sum_nh_{\psi}{(n)}\sqrt{2}\phi(2t-n) ψ(t)=∑nhψ(n)2ϕ(2t−n)
ps: 为了博客更生动形象,使用了不少来自参考文献的图片,在此感谢。若有侵犯,请联系删除。
参考文献
[1] Why wavelet?
[2] 冈萨雷斯 数字图像处理 第3版
[3] http://math.bu.edu/people/mkon/ma717/L12HaarWavelet.pdf
[4] http://www.ws.binghamton.edu/fowler/EECE523/Ch_15_2%20Wavelet%20Example.pdf
[5] https://slideplayer.com/slide/7537671/
[6] https://mathworld.wolfram.com/HaarFunction.html
[7] 知乎:通过Haar小波认识离散小波变换
[8] 哈工大,冉启文,小波变换与分数傅里叶变换理论及应用