写在前面
学习代码都记录在个人github上,欢迎关注~
Matlab机器人工具箱版本9.10
在前面的博文中:
基于抛物线过渡(梯形加减速)的空间直线插补算法与空间圆弧插补算法(Matlab)
我使用了抛物线过渡(也就是梯形加减速)作为空间插补算法的速度规划方法,但是梯形曲线的缺点也很明显,即加速度不连续,速度过渡不平滑,容易造成机械系统冲击。下面我尝试了S型加减速曲线的规划方法并结合到空间插补算法中,仿真效果还可以,加速度曲线连续,更柔和,适用于精度速度要求更高的场合。
空间直线插补:

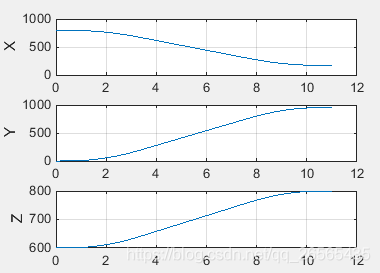
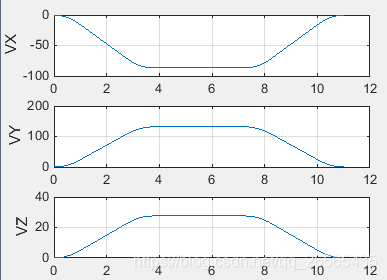
空间圆弧插补:
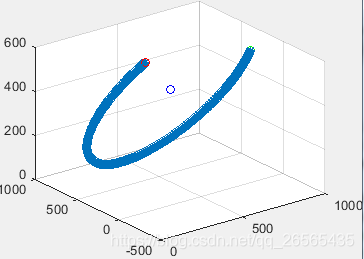
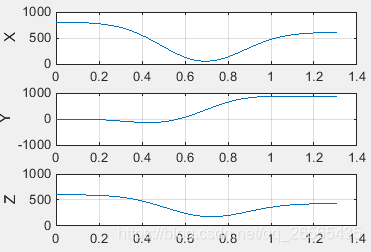
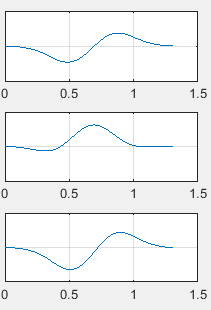
直观插补:

带约束S型速度规划
预备知识:
机器人学回炉重造(6):关节空间规划方法——梯形加减速(与抛物线拟合的线性函数)、S型曲线规划
参照基于抛物线过渡(梯形加减速)的空间直线插补算法与空间圆弧插补算法(Matlab)中归一化参数思想,将归一化参数计算函数中的梯形加减速方法换成S型加减速法。此时,定义归一化时间算子:
λ ( t ) = s ( t ) − s ( 0 ) L \lambda( t ) = \frac { s ( t ) - s ( 0 ) } { L } λ(t)=Ls(t)−s(0)
其中, t ∈ [ 0 , T ] t \in [ 0 , T ] t∈[0,T], s ( t ) s(t) s(t)是S型曲线中位移在全局时间坐标下的函数, L L L是机器人执行器末端经过的距离。
空间直线插补与空间圆弧插补
位置插补与姿态插补需要分开讨论。
位置插补
假设机器人末端由P1点沿直线运动到P2点, ( x 1 , y 1 , z 1 ) \left(x_{1}, y_{1}, z_{1}\right) (x1,y1,z1)分别为起点P1的位置, ( x 2 , y 2 , z 2 ) \left(x_{2}, y_{2}, z_{2}\right) (x2,y2,z2)为终点P2的位置, ( x i , y i , z i ) \left(x_{i}, y_{i}, z_{i}\right) (xi,yi,zi)为中间插补点Pi的位置。
各个插值点位置坐标向量为:
{ x = x 1 + λ Δ x y = y 1 + λ Δ y z = z 1 + λ Δ z \left\{\begin{array}{l}{x=x_{1}+\lambda \Delta x} \\ {y=y_{1}+\lambda \Delta y} \\ {z=z_{1}+\lambda \Delta z}\end{array}\right. ⎩⎨⎧x=x1+λΔxy=y1+λΔyz=z1+λΔz
其中, λ \lambda λ是归一化时间因子, ( Δ x , Δ y , Δ z ) (\Delta x, \Delta y, \Delta z) (Δx,Δy,Δz)表示首末位置间的位置增量,其解为:
{ Δ x = x 2 − x 1 Δ y = y 2 − y 1 Δ z = z 2 − z 1 \left\{\begin{array}{l}{\Delta x=x_{2}-x_{1}} \\ {\Delta y=y_{2}-y_{1}} \\ {\Delta z=z_{2}-z_{1}} \end{array}\right. ⎩⎨⎧Δx=x2−x1Δy=y2−y1Δz=z2−z1
基于单位四元数的姿态插补
预备知识:
已知起点S、终点D的齐次变换矩阵(位姿)分别为 T S T_S TS和 T D T_D TD,则姿态插补步骤如下:
-
从齐次变换矩阵中提取出各自的旋转矩阵 R S R_S RS和 R D R_D RD,并将其转换为四元数 Q s Q_s Qs和 Q d Q_d Qd;
-
姿态四元数插补公式为:
Q k ( t ) = Slerp ( Q s , Q d , t ) = sin [ ( 1 − λ ( t ) ) θ ] sin θ Q s + sin [ λ ( t ) θ ] sin θ Q d Q_{k}(t)=\operatorname{Slerp}\left(Q_{s}, Q_{d}, t\right)=\frac{\sin [(1-\lambda(t)) \theta]}{\sin \theta} Q_{s}+\frac{\sin [\lambda(t) \theta]}{\sin \theta} Q_{d} Qk(t)=Slerp(Qs,Qd,t)=sinθsin[(1−λ(t))θ]Qs+sinθsin[λ(t)θ]Qd
式中, θ = a r c c o s ( Q s ⋅ Q d ) \theta=arccos(Q_{s} \cdot Q_{d}) θ=arccos(Qs⋅Qd); -
将四元数 Q k ( t ) Q_{k}(t) Qk(t)转换为旋转矩阵 R k R_{k} Rk,将 R k R_{k} Rk和位置插补得到的 P k P_{k} Pk组合得到各插值点对应的齐次变换矩阵 T k T_{k} Tk;
-
带入逆运动学计算,得到各关节角度变量,进行插补运动。
规划插补流程
基于带约束S型加减速曲线的插补算法流程图如下:

Matlab实现代码
和前面博文的联系非常紧密,部分函数并未展出。
% 归一化处理
% S型加减速曲线
% 输入参数:机械臂末端运动总位移(角度)pos
% 机械臂末端线速度(角速度)初始v0,终止v1,最大速度vmax
% 最大加减速度amax、最大加加速度jmax
% 插补周期t
% 返回值: 插值点数N
function [lambda, N] = Normalization_S(pos, v0, v1, vmax, amax, jmax, t)
% S曲线参数计算(S型速度规划,又称七段式轨迹)
% function para = STrajectoryPara(q0, q1, v0, v1, vmax, amax, jmax)
q0 = 0; q1 = pos;
para = STrajectoryPara(q0, q1, v0, v1, vmax, amax, jmax); % 获取S曲线参数
% 总的规划时间
T = para(1) + para(2) + para(3)
% 等时插补
N = ceil(T / t);
j = 1;
for i = 0 : t: T
q(j) = S_position(i, para(1), para(2), para(3), para(4), para(5), para(6), para(7), para(8), para(9), para(10), para(11), para(12), para(13), para(14), para(15), para(16));
% qd(j) = S_velocity(i, para(1), para(2), para(3), para(4), para(5), para(6), para(7), para(8), para(9), para(10), para(11), para(12), para(13), para(14), para(15), para(16));
lambda(j) = q(j) / pos;
j = j + 1;
end
end
% 空间单一直线位置插补与单元四元数姿态插补 + 梯形加减速归一化处理/S型加减速曲线归一化处理
% 参数:起点S位置, 终点D位置
% 起点S的单元四元数Qs,终点的单元四元数Qd
% 起始速度v0,终止速度v1,最大速度vmax,最大加速度amax,最大加加速度jmax
% 插补周期t
% 返回值:插值点位置、单元四元数、插值点数
function [x y z qk N] = SpaceLine_Q(S, D, Qs, Qd, v0, v1, vmax, amax, jmax, t)
x1 = S(1); y1 = S(2); z1 = S(3);
x2 = D(1); y2 = D(2); z2 = D(3);
P = 1; % 插值参数,增加插值点数,避免过小
% 总位移S
s = sqrt(power(x2 - x1, 2) + power(y2 - y1, 2) + power(z2 - z1, 2))
% 插值点数N
% N = ceil(P*s / vs)
% 求归一化参数:梯形加减速曲线
% function lambda = Normalization(pos, vel, accl, N)
% lambda = Normalization(s, vs, a, N);
% 求归一化参数:S型加减速曲线
% function lambda = Normalization_S(pos, v0, v1, vmax, amax, jmax, N)
[lambda, N] = Normalization_S(s, v0, v1, vmax, amax, jmax, t);
delta_x = x2 - x1;
delta_y = y2 - y1;
delta_z = z2 - z1;
% 计算两个四元数之间的夹角
dot_q = Qs.s*Qd.s + Qs.v(1)*Qd.v(1) + Qs.v(2)*Qd.v(2) + Qs.v(3)*Qd.v(3);
if (dot_q < 0)
dot_q = -dot_q;
end
for i = 1: N
% 位置插补
x(i) = x1 + delta_x*lambda(i);
y(i) = y1 + delta_y*lambda(i);
z(i) = z1 + delta_z*lambda(i);
% 单位四元数球面线性姿态插补
% 插值点四元数
if (dot_q > 0.9995)
k0 = 1-lambda(i);
k1 = lambda(i);
else
sin_t = sqrt(1 - power(dot_q, 2));
omega = atan2(sin_t, dot_q);
k0 = sin((1-lambda(i)*omega)) / sin(omega);
k1 = sin(lambda(i)*omega) / sin(omega);
end
qk(i) = Qs * k0 + Qd * k1;
end
end
% 空间单一圆弧位置插补与单位四元数姿态插补 + 梯形加减速归一化处理/S型加减速曲线归一化处理
% 参数: 起点S位置, 中间点M位置, 终点D位置
% 起点S和终点D的单位四元数Qs_,Qd_
% 起始速度v0,终止速度v1,最大速度vmax,最大加速度amax,最大加加速度jmax
% 插值周期t
% 返回值:插值点位置、单元四元数、插值点数
% 方便起见,角速度和角加速度均为角度制
function [x y z qk N] = SpaceCircle_Q(S, M, D, Qs_, Qd_, v0, v1, vmax, amax, jmax, t)
x1 = S(1); x2 = M(1); x3 = D(1);
y1 = S(2); y2 = M(2); y3 = D(2);
z1 = S(3); z2 = M(3); z3 = D(3);
A1 = (y1 - y3)*(z2 - z3) - (y2 - y3)*(z1 - z3);
B1 = (x2 - x3)*(z1 - z3) - (x1 - x3)*(z2 - z3);
C1 = (x1 - x3)*(y2 - y3) - (x2 - x3)*(y1 - y3);
D1 = -(A1*x3 + B1*y3 + C1*z3);
A2 = x2 - x1;
B2 = y2 - y1;
C2 = z2 - z1;
D2 = -((x2^2 - x1^2) + (y2^2 - y1^2) + (z2^2 - z1^2)) / 2;
A3 = x3 - x2;
B3 = y3 - y2;
C3 = z3 - z2;
D3 = -((x3^2 - x2^2) + (y3^2 - y2^2) + (z3^2 - z2^2)) / 2;
A = [A1, B1, C1; A2, B2, C2; A3, B3, C3]
b = [-D1, -D2, -D3]'
% 圆心
C = Gauss_lie(3, A, b)
x0 = C(1); y0 = C(2); z0 = C(3);
plot3(x0, y0, z0, 'bo')
hold on
% 外接圆半径
r = sqrt(power(x1 - x0, 2) + power(y1 - y0, 2) + power(z1 - z0, 2));
% 新坐标系Z0的方向余弦
L = sqrt(A1^2 + B1^2 + C1^2);
ax = A1 / L; ay = B1 / L; az = C1 / L;
% 新坐标系X0的方向余弦
nx = (x1 - x0) / r;
ny = (y1 - y0) / r;
nz = (z1 - z0) / r;
% 新坐标系Y0的方向余弦
o = cross([ax, ay, az], [nx, ny, nz]);
ox = o(1);
oy = o(2);
oz = o(3);
% 相对于基座标系{O-XYZ}, 新坐标系{C-X0Y0Z0}的坐标变换矩阵
T = [nx ox ax x0;
ny oy ay y0;
nz oz az z0;
0 0 0 1]
T_ni = T^-1
% 求在新坐标系{C-X0Y0Z0}下S、M和D的坐标
S_ = (T^-1)*[S'; 1]
M_ = (T^-1)*[M'; 1]
D_ = (T^-1)*[D'; 1]
x1_ = S_(1) , y1_ = S_(2), z1_ = S_(3)
x2_ = M_(1), y2_ = M_(2), z2_ = M_(3)
x3_ = D_(1), y3_ = D_(2), z3_ = D_(3)
% 判断圆弧是顺时针还是逆时针,并求解圆心角
if (atan2(y2_, x2_) < 0)
angle_SOM = atan2(y2_, x2_) + 2*pi;
else
angle_SOM = atan2(y2_, x2_);
end
if (atan2(y3_, x3_) < 0)
angle_SOD = atan2(y3_, x3_) + 2*pi;
else
angle_SOD = atan2(y3_, x3_);
end
% 逆时针
if (angle_SOM < angle_SOD)
flag = 1;
theta = angle_SOD % 圆心角
end
% 顺时针
if (angle_SOM >= angle_SOD)
flag = -1;
theta = 2*pi - angle_SOD % 圆心角
end
% 插补点数N
% P = 1; %插补参数,增加插值点数,避免过小
% ws = ws*pi / 180; % 角度换成弧度
% a = a*pi / 180;
% N = ceil(P*theta / ws);
% % 求归一化参数:梯形加减速曲线
% lambda = Normalization(theta, ws, a, N);
% 求归一化参数:S型加减速曲线
% function lambda = Normalization_S(pos, v0, v1, vmax, amax, jmax, N)
[lambda, N] = Normalization_S(theta, v0, v1, vmax, amax, jmax, t);
% 插补原理: 在新平面上进行插补(简化)
% 在新坐标系下z1_,z2_,z3_均为0,即外接圆在新坐标系的XOY平面内
% 此时转化为平面圆弧插补问题
delta_ang = theta;
% 计算两个四元数之间的夹角
dot_q = Qs_.s*Qd_.s + Qs_.v(1)*Qd_.v(1) + Qs_.v(2)*Qd_.v(2) + Qs_.v(3)*Qd_.v(3);
if (dot_q < 0)
dot_q = -dot_q;
end
for i = 1: N
% 位置插补
x_(i) = flag * r * cos(lambda(i)*delta_ang);
y_(i) = flag * r * sin(lambda(i)*delta_ang);
P = T*[x_(i); y_(i); 0; 1];
x(i) = P(1);
y(i) = P(2);
z(i) = P(3);
% 单位四元数球面线性姿态插补
% 插值点四元数
if (dot_q > 0.9995)
k0 = 1-lambda(i);
k1 = lambda(i);
else
sin_t = sqrt(1 - power(dot_q, 2));
omega = atan2(sin_t, dot_q);
k0 = sin((1-lambda(i))*omega) / sin(omega);
k1 = sin(lambda(i)*omega) / sin(omega);
end
qk(i) = Qs_ * k0 + Qd_ * k1;
end
end
不足之处
- 圆弧的姿态插补只严格通过了起始姿态和终点姿态,没有经过中间姿态;
- 无法达到时间最优。
参考文献
[1]刘鹏飞,杨孟兴,宋科,段晓妮.‘S’型加减速曲线在机器人轨迹插补算法中的应用研究[J].制造业自动化,2012,34(20):4-8+11.
[2]李振娜,王涛,王斌锐,郭振武,陈迪剑.基于带约束S型速度曲线的机械手笛卡尔空间轨迹规划[J].智能系统学报,2019,14(04):655-661.
[3]王添. 基于单位四元数机器人多姿态轨迹平滑规划[D].天津工业大学,2018.
[4]季晨. 工业机器人姿态规划及轨迹优化研究[D].哈尔滨工业大学,2013.