翻译了一篇博文,原文pdf可后台回复“最小二乘”下载。
当面试时问到最小二乘损失函数的基础数学知识时,你会怎么回答?
Q: 为什么在回归中将误差求平方?
A:因为可以把所有误差转化为正数。
Q:为什么不直接用绝对值将误差转为正数?
A:因为绝对值函数不是处处可导。
Q:这个在数值算法中不成问题,LASSO回归中就用到了绝对值。而且,为什么不是计算x的4次方,或log(1+x^2)?将误差进行乘方计算有什么好处?
A:呃...
基础:贝叶斯定理和“最可能假设”
贝叶斯定理可能是机器学习和人工智能涉及到的概率论知识中,最有影响的定理。贝叶斯公式如下:
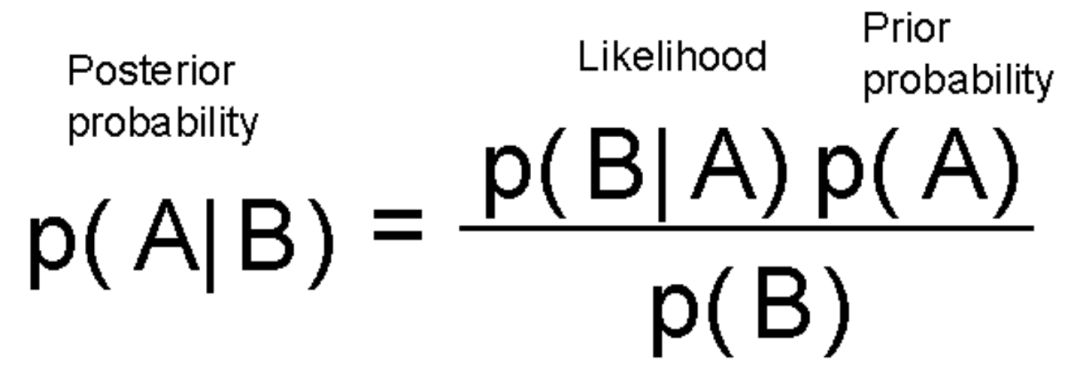
这个式子告诉我们,根据数据(可能性函数),更新假设(先验概率),并且将先验概率的更新程度分配给后验概率。
下面我们用数据科学符号重新写一下这个公式,用D表示数据,h表示假设。
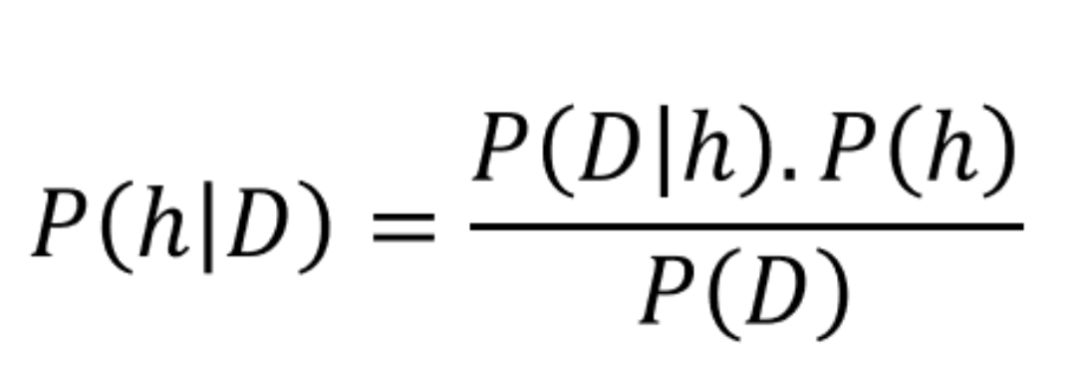
一般来说,我们有一个大的(通常是无限的)假设空间,即许多假设可供选择。贝叶斯推理的本质是通过检验数据,使最可能产生观测数据的假设概率最大化。我们想求P(h|D)的argmax,即给定D下,h概率最大。
捷径:最大似然
上述方程看似简单,但在实践中计算起来却很难。因为在复杂的概率分布函数上求积分的假设空间非常大,且计算复杂。然而,在我们寻找“给定数据的最可能假设”的过程中,我们可以进一步简化它。
简化后的最大似然假设如下(式一):
这意味着最可能的假设是观测数据的条件概率达到最大值的假设。
另一个问题:噪音
在进行简单的回归时,通常都会将误差进行最小二乘处理,且这个方法在几乎所有有监督算法中都有使用,如:线性模型,决策树等。结果表明,最小二乘误差与贝叶斯推理的关键联系在于误差或残差的假设性质。测量/观测数据决不是无误差的,并且总是存在与数据相关联的随机噪声,这可以认为是数据特征重要性的信号。机器学习算法的任务是通过从噪声中分离信号来估计/近似可能产生数据的函数。但是我们怎么描述这种噪音的性质?事实证明,噪声可以做为建模中等一个随机变量。因此,我们可以把我们的选择的概率分布与这个随机变量联系起来。最小二乘优化的一个关键假设是残差上的概率分布是我们信任的老朋友——高斯正态。也就是说,在监督学习训练集中的每个点d,都可以写成一个未知函数f(x)和误差项的和,且这个误差项服从正态分布(式二):
从这个理论中,我们很容易得出,最大可能假设是最小化最小平方误差的假设。
基于极大似然假设的最小二乘法推导


上面公式说明,从有监督训练数据集的误差分布在高斯正态分布的假设出发,训练数据的最大似然假设是最小化最小平方误差损失函数。学习算法的类型没有任何假设,适用于从简单线性回归到深度神经网络的任何算法。
下面是一个典型的线性回归拟合方案。贝叶斯推理论证对这个模型进行了验证,为误差平方的选择提供了可信度。
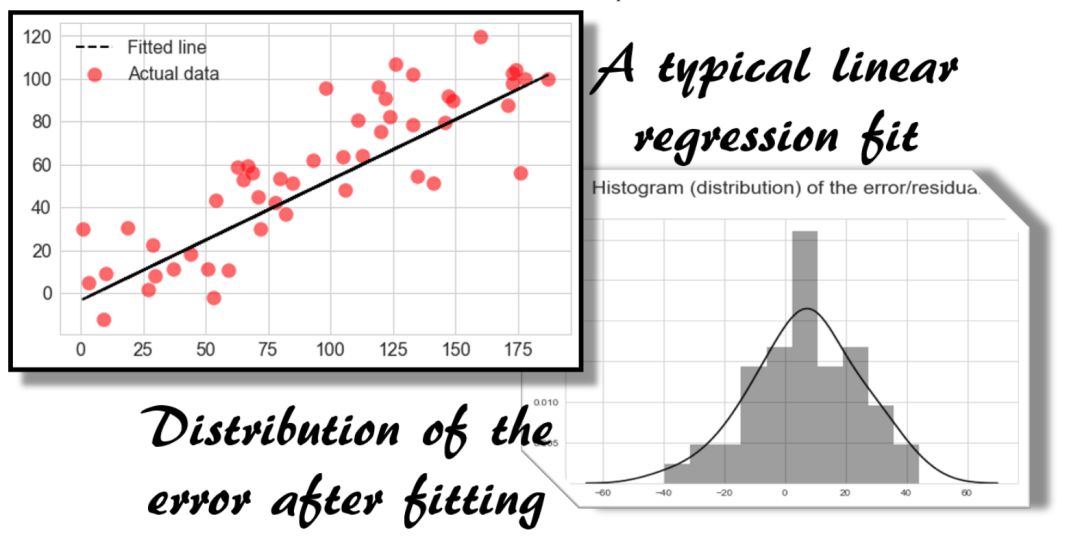
你可以质疑关于正态分布误差项的假设的有效性。但在大多数情况下,它是有效的。这源于中心极限定理(CLT),因为误差或噪声从来不是由单个基础过程产生的,而是由多个子过程的组合影响产生的。当大量随机子过程合并时,它们的平均值服从正态分布(来自CLT)。
总结
最大似然估计(MLE)是针对给定数据集得出最可能假设的有力技术,如果我们能够作出统一的先验假设,即在开始时,所有假设都同样可能。
如果假设机器学习任务中的每个数据点是真函数与一些正态分布的随机噪声变量之和,则可以得出最大概率假设是最小化平方损失函数的假设。
这一结论与机器学习算法的性质无关。
然而,另一个隐含的假设是数据是独立的,使我们能够将整体概率作为部分概率的组合。这也突显了在机器学习模型的构建应消除训练样本之间的共线性的重要性。