一元二次方程高精度实数根(C语言)

一、问题描述

  已知一元二次方程$a{x}^2+bx+c=0(a\ne 0)$，求方程的实数根。在数学上，我们很容易可以得到方程的实数根为：
$$x_1=\frac{-b+\sqrt{b^2-4ac}}{2a}\text{\hspace{1em}(1)}$$
$$x_2=\frac{-b-\sqrt{b^2-4ac}}{2a}\text{\hspace{1em}(2)}$$
  其中，$b^2-4ac\ge 0$
  然而，在计算机上，由于计算机字长的限制，有些浮点数无法绝对精确地存储。并且，一些计算过程可能会导致精度损失。例如接下来这两个例子。
  $(A)$设有两个数$p=3.1415926536$和$q=3.1415957341$，两者几乎相等，而且都有11位有效数字精度。它们的差为$p-q=-0.0000030805$，只有5位有效数字精度！
  $(B)$设$f(x)=x(\sqrt{x+1}-\sqrt{x}),g(x)=\frac{x}{\sqrt{x+1}+\sqrt{x}}$。显然，当$x\ge 0$时，$f(x)$可以通过分母有理化得到$g(x)$，在数学上两者是等价的。现在，我们采用6位有效数字精度和舍入法比较$f(500)$与$g(500)$的计算结果。$f(500)=500\times (\sqrt{501}-\sqrt{500})=500\times (22.3830-22.3607)=500\times 0.0223=11.1500$。$g(500)=\frac{500}{\sqrt{501}+\sqrt{500}}=\frac{500}{22.3830+22.3607}=\frac{500}{44.7437}=11.1748$。$g(500)$比$f(500)$计算精度更高！(真实值为11.174755300747198…，舍入到6位有效数字，与$g(500)$的计算值相同）
  精度损失的现象在我们编程过程中很有可能会出现，有时可能会使计算结果与正确结果大相径庭，产生灾难性的后果，我们必须引起足够重视。精度损失的现象有时候是没办法避免的，有时候则可以通过一些数值计算算法或技巧来避免。显然，式$(1)$和式$(2)$的分子在一定条件下，可能是两个相近的数相减，影响计算精度。那么，如何编写一个计算精度较高的程序来求一元二次方程的实数根呢？

二、推导步骤

  编写一个计算精度较高的程序来求一元二次方程$a{x}^2+bx+c=0(a\ne 0)$的实数根，至少需要考虑两种情形：$(A)\left|b\right|\approx \sqrt{b^2-4ac}(B)c=0$
  $(A)$若$\left|b\right|\approx \sqrt{b^2-4ac}$，当$b>0$时，式$(1)$中，$-b+\sqrt{b^2-4ac}$会导致计算精度损失，对式$(1)$分子有理化得：
$$x_1=\frac{-2c}{b+\sqrt{b^2-4ac}}\text{\hspace{1em}(3)}$$
  当$b\le 0$时，式$(2)$中，$-b-\sqrt{b^2-4ac}$会导致计算精度损失，对式$(2)$分子有理化得：
$$x_2=\frac{-2c}{b-\sqrt{b^2-4ac}}\text{\hspace{1em}(4)}$$
  $(B)$若$c=0$，在数学上，$\sqrt{b^2-4ac}=\left|b\right|$，但计算机在数值计算过程中，对$b$进行了开方和平方根运算，会引入计算误差(或截断误差)和舍入误差，导致此时$\sqrt{b^2-4ac}\ne \left|b\right|$，使方程根的计算误差变大。因而，当$c=0$时，需特殊处理，此时方程的两实数根为：

$$\{\begin{array}{c}{x}_1=0\\ x_2=\frac{-b}{a}\end{array}\text{\hspace{1em}(5)}$$

三、$C$代码

#include <math.h>
#include <float.h>
#include <stdio.h>

#define UINT32 unsigned int
#define ERR_NO_ERROR 0x00000000
#define ERR_NAN 0x00000001
#define ERR_INF 0x00000002
#define MAX(a, b) ((a) > (b)) ? (a) : (b)
#define MIN(a, b) ((a) < (b)) ? (a) : (b)

/*************************************************
Function: is_number
Description: 判断浮点数是否为nan
Input: 浮点数x
Output: 无
Return: 若浮点数x为nan返回0，否则返回1
Author: Marc Pony([email protected])
*************************************************/
int is_number(float x) 
{
    
     
	return (x == x);
}

/*************************************************
Function: is_finite_number
Description: 判断浮点数是否为inf
Input: 浮点数x
Output: 无
Return: 若浮点数x为inf返回0，否则返回1
Author: Marc Pony([email protected])
*************************************************/
int is_finite_number(float x) 
{
    
     
	return (x >= -FLT_MAX && x <= FLT_MAX);
}

/*************************************************
Function: solve_quadratic_equation
Description: 求一元二次方程(a*x^2 + b*x + c = 0)的所有实数根
Input: 方程的系数 p = {c, b, a}
Output: 方程的所有实数根x, 实数根的个数rootCount
Return: 错误号
Author: Marc Pony([email protected])
*************************************************/
UINT32 solve_quadratic_equation(float p[], float x[], int *rootCount)
{
    
    
	int i;
	float a, b, c, delta, sqrtDelta;
	const float ZERO = FLT_MIN;  // min normalized positive value（1.175494351e-38F）
	const float EPS = FLT_MIN;
	UINT32 errNo = ERR_NO_ERROR;

	*rootCount = 0;
	for (i = 0; i < 3; i++)
	{
    
    
		if (!is_number(p[i]))
		{
    
    
			errNo = ERR_NAN;
			return errNo;
		}
		if (!is_finite_number(p[i]))
		{
    
    
			errNo = ERR_INF;
			return errNo;
		}
	}

	a = p[2];
	b = p[1];
	c = p[0];
	
	if (fabs(a - 0.0) < EPS)
	{
    
    
		if (fabs(b - 0.0) > EPS)
		{
    
    
			x[0] = -c / b;
			*rootCount = 1;
		}
	}
	else
	{
    
    
		b /= a;
		c /= a;
		a = 1.0;

		delta = b * b - 4.0 * a * c;
		if (delta > ZERO)
		{
    
    
			if (fabs(c - 0.0) < EPS)	//若c = 0,由于计算误差,sqrt(b*b - 4*a*c）不等于|b|
			{
    
    
				x[0] = 0.0;
				x[1] = -b / a;
			}
			else
			{
    
    
				sqrtDelta = sqrt(delta);
				if (b > 0.0)
				{
    
    
					x[0] = (-2.0 * c) / (b + sqrtDelta);	//避免两个很接近的数相减,导致精度丢失
					x[1] = (-b - sqrtDelta) / (2.0 * a);
				}
				else
				{
    
    
					x[0] = (-b + sqrtDelta) / (2.0 * a);
					x[1] = (-2.0 * c) / (b - sqrtDelta);	//避免两个很接近的数相减,导致精度丢失
				}
			}
			*rootCount = 2;
		}
		else if (fabs(delta - 0.0) < EPS)
		{
    
    
			x[0] = x[1] = -b / (2.0 * a);
			*rootCount = 2;
		}
		else
		{
    
    
			*rootCount = 0;
		}
	}
	return errNo;
}

void main(void)
{
    
    
	float x[2], p[3];
	int rootCount;
	float x1, x2, a, b, c;
	UINT32 errNo = ERR_NO_ERROR;

	//一元二次方程测试
	//（1）(x - 1000)*(x - 0.001) = x^2 - 1000.001*x + 1 = 0
	a = 1;
	b = -1000.001;
	c = 1;

	//(2) 3*x ^ 2 - 1000000*x + 0 = 0
	//a = 3;
	//b = -1000000;
	//c = 0;

	//(3) 1.0e-10*x^2 - 2.0e-10*x + 1.0e-10 = 0
	//a = 1.0e-10;
	//b = -2.0e-10;
	//c = 1.0e-10;

	p[0] = c;
	p[1] = b;
	p[2] = a;
	errNo = solve_quadratic_equation(p, x, &rootCount);
	x1 = (-b - sqrt(b * b - 4.0 * a * c)) / (2.0 * a);
	x2 = (-b + sqrt(b * b - 4.0 * a * c)) / (2.0 * a);

	printf("原始方法求得方程的根:x1=%f, x2=%f\n本文方法求得方程的根:x1=%f, x2=%f\n",
		MIN(x1, x2), MAX(x1, x2), MIN(x[0], x[1]), MAX(x[0], x[1]));
}

  (1)当$a=1,b=-1000.001,c=1$时，方程根的准确值为:0.001和1000，程序运行结果：

  (2)当$a=3,b=-1000000,c=0$时，方程根的准确值为:0和333333.33…，程序运行结果：

  (3)当$a=1.0e^{-10},b=-2.0e^{-10},c=1.0e^{-10}$时，方程根的准确值为:1和1，程序运行结果：

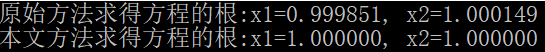
四、总结

  一元二次方程实数根的c语言实现，在很多人看来非常简单，根本不值一提，然而就是这么简单的问题，要写出计算精度高、简洁优雅、可读性强、健壮的代码也不是一件简单的事。

五、参考文献/资料

Numerical Methods Using MATLAB Fourth Edition. John Mathews, Kurtis D.Fink
数值方法(MATLAB版)(第四版) 周璐，陈渝，钱方等译