提升(boosting)方法是一中可将弱学习器提升为强学习器的算法。这中算法的工作机制类似:先从初始训练集训练出一个基学习器,再根据基学习器的表现对训练样本分布进行调整,使得先前基学习器做错的训练样本在后续受到更多关注,然后基于调整后的样本分布来训练下一个基学习器;如此重复进行,直至基学习器数目达到事先指定的值T,最终将这T个基学习器进行加权结合。
一 AdaBoost算法
对于分类问题而言,给定一个训练样本集,求比较粗糙的分类规则(弱分类器)要比求精确的分类规则(强分类器)容易得多。提升方法就是从弱学习算法出发,反复学习,得到一系列弱分类器(又称为基本分类器),然后组合这些弱分类器,构成一个强分类器。大多数的提升方法都是改变训练数据的概率分布(训练数据的权值分布),针对不同的训练数据分布调用弱学习算法学习一系列弱分类器。
这样,对提升方法来说,有个两个问题需要回答:一是在每一轮如何改变训练数据的权值或概率分布;二是如何将弱分类器组合成一个强分类器。
关于第一个问题,AdaBoost的做法是,提高那些被前一轮弱分类器错误分类样本的权值,而降低那些被正确分类样本的权值。至于第二个问题,即弱分类器的组合,AdaBoost采取加权多数表决的方法,具体地,加大分类错误率小的弱分类器的权值,使其在表决中起较大的作用,减小分类错误率大的弱分类器的权值,使其在表决中起较小的作用。
(1)算法
假设给定一个二类分类的训练数据集:D={(
,
),(
,
),⋯,(
,
),⋯,(
,
)}
其中,每个样本点由实例与标记组成。实例
X⊆
,标记
∈Y=−1,+1,X 是实例空间,Y是标记集合。AdaBoost利用以下算法,从训练数据中学习一系列弱分类器或基本分类器,并将这些弱分类器组合成为一个强分类器。


证明:
首先假设训练数据集具有均匀的权值分布,即每个训练样本在基本分类器的学习中作用相同,这一假设保证在m=1时能够在原始数据上学习基本分类器
(x)。
由8.2可知,错误分类的样本,权值越大,分类误差率也越大。前一次因分类错而增大权值的样本,若在这一次仍继续错误,则分类误差率会增大,通过式8.4影响系数,使这时得到的基本分类器在最终分类器中的作用减小。
由8.2可知,当分类误差率
≤1/2时,
≥0,并且
随着
的减小而增大,所以分类误差率越小的基本分类器在最终分类器中的作用越大。
式8.4可写成:
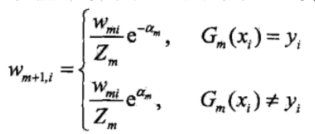
由此可知,被基本分类器
(x)误分类样本的权值得以扩大,而被正确分类样本的权值却得以缩小,这样一来,那些没有得到正确分类的数据,由于其权值的加大而受到后一轮的弱分类器的更大关注。
循环M次,得到M个基本分类器及对应的系数,最后,利用基本分类器的线性组合构建最终分类器。


import numpy as np
#首先我想介绍的是决策树桩中的init,接受3个参数,一个是axis,表示这个决策树桩是按哪个维度划分,一个是threshold,表示这个决策树桩是按什么阈值划分,还有一个是flag,这个我要稍微说明下,有了阈值还不够成为一个分类器。比如是x>=2.5为1,还是x>=2.5为-1,所以需要这个标志来说明是哪种情况。在这个代码中,当flag=True时, x>=threshold=1, 否则为-1。
class SingleDecisionTree: #决策树桩
def __init__(self, axis=0, threshold = 0, flag = True):
self.axis = axis
self.threshold = threshold
self.flag = flag #flag=True, x>=threshold=1, 否则为-1
def preditct(self, x):
if (self.flag == True):
return -1 if x[self.axis] >= self.threshold else 1
else:
return 1 if x[self.axis] >= self.threshold else -1
def preditctArr(self, dataSet):
result = list()
for x in dataSet:
if (self.flag == True):
result.append(-1 if x[self.axis] >= self.threshold else 1)
else:
result.append(1 if x[self.axis] >= self.threshold else -1)
return result
class Adaboost:
def train(self, dataSet, labels):
N = np.array(dataSet).shape[0] #样本总数
M = np.array(dataSet).shape[1] #样本维度
self.funList = list() # 存储alpha和决策树桩
D = np.ones((N, 1)) / float(N) #(1)数据权值分布
#得到基本分类器 开始
L = 0.5
minError = np.inf #初始化误差大小为最大值(因为要找最小值)
minTree = None #误差最小的分类器
while minError > 0.01:
for axis in range(M):
min = np.min(np.array(dataSet)[:, axis]) #需要确定阈值的最小值
max = np.max(np.array(dataSet)[:, axis]) #需要确定阈值的最大值
for threshold in np.arange(min, max, L): #左开右闭
tree = SingleDecisionTree(axis=axis, threshold = threshold, flag=True) #决策树桩
em = self.calcEm(D, tree, dataSet, labels) #误差率
if (minError > em): #选出最小的误差,以及对应的分类器
minError = em
minTree = tree
tree = SingleDecisionTree(axis=axis, threshold = threshold, flag=False) #同上,不过flag的作用要知道
em = self.calcEm(D, tree, dataSet, labels)
if (minError > em):
minError = em
minTree = tree
alpha = (0.5) * np.log((1 - minError) / float(minError)) #p139(8.2)
self.funList.append((alpha, minTree)) #把alpha和分类器写到列表
D = np.multiply(D, np.exp(np.multiply(-alpha * np.array(labels).reshape((-1, 1)), np.array(minTree.preditctArr(dataSet)).reshape((-1, 1))))) / np.sum(np.multiply(D, np.exp(np.multiply(-alpha * np.array(labels).reshape((-1, 1)), np.array(minTree.preditctArr(dataSet)).reshape((-1, 1)))))) #对应p139的公式(8.4)
def predict(self, x): #预测方法
sum = 0
for fun in self.funList: #书上最终分类器的代码
alpha = fun[0]
tree = fun[1]
sum += alpha * tree.preditct(x)
return 1 if sum > 0 else -1
def calcEm(self, D, Gm, dataSet, labels): #计算误差
# value = list()
value = [0 if Gm.preditct(row) == labels[i] else 1 for (i, row) in enumerate(dataSet)]
return np.sum(np.multiply(D, np.array(value).reshape((-1, 1))))
if __name__ == '__main__':
# dataSet = [[0], [1], [2], [3], [4], [5], [6], [7], [8], [9]] #例8.1的数据集
# labels = [1, 1, 1, -1, -1, -1, 1, 1, 1, -1]
dataSet = [[0, 1, 3], [0, 3, 1], [1, 2, 2], [1, 1, 3], [1, 2, 3], [0, 1, 2], [1, 1, 2], [1, 1, 1], [1, 3, 1], [0, 2, 1]] #p153的例子
labels = [-1, -1, -1, -1, -1, -1, 1, 1, -1, -1]
adaboost = Adaboost()
adaboost.train(dataSet, labels)
# for x in dataSet:
# print(adaboost.predict(x))
print(adaboost.predict([1, 3, 2]))
二、前向分步算法
加法模型:
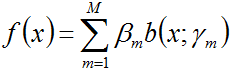
其中,b(
;
)称为基函数,
称为基函数的参数,
称为基函数的系数。
在给定训练数据及损失函数L(
,
)的条件下,学习加法模型
成为经验风险极小化问题,即损失函数极小化问题:
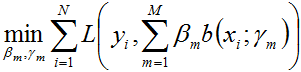
随后,该问题可以作如此简化:从前向后,每一步只学习一个基函数及其系数,逐步逼近上式,即:每步只优化如下损失函数:
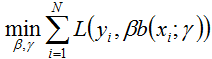
这个优化方法便就是所谓的前向分步算法。


三 提升树算法
提升树是以分类树或回归树为基本分类器的提升方法。
(1)提升树模型
提升方法实际采用加法模型(即基函数的线性组合)与前向分布算法。以决策树为基函数的提升方法称为提升树。
对分类问题决策树是二叉分类树;对回归问题决策树是二叉回归树。提升树模型可以表示为决策树的加法模型:
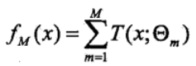
其中, ( ; )表示决策树; 为决策树的参数;M为树的个数。
(2)提升树算法
提升树算法采用前向分步算法,首先确定初始提升树
(
)=0,第
步的模型是
其中, ( )为当前模型,通过经验风险极小化确定下一棵决策树的参数
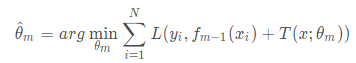
由于树的线性组合可以很好地拟合训练数据,即使数据中的输入与输出之间的关系很复杂也如此,所以提升树是一个高功能的学习算法。
(3)二类分类问题提升树
对于二类分类问题,提升树算法只需将AdaBoost算法1中的基本分类器限制为二类分类树即可,可以说这时的提升树算法是AdaBoost算法的特殊情况,这里不再细述。
(4)回归问题的提升树
已知一个训练集
{(
,
),(
,
)…(
,
)},
∈
,
为输入空间,
∈
,Y为输出空间。在决策树一文中我们已经讨论了回归树的问题。如果将输入空间
划分为
个互不相交的区域
⋯
,并且在每个区域上确定输出的常量
,
=
⋯
,那么树可表示为
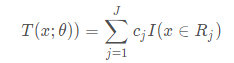
其中,参数 =( ) ( ) ⋯ ( )表示树的区域划分和各区域上的常数。 是回归树的复杂度即叶结点个数。
回归问题提升树使用以下前向分步算法:
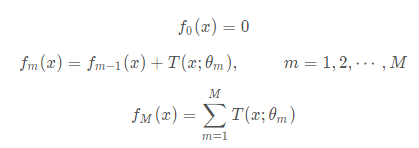
在前向分步算法的第 步,给定当前模型 x ,需求解
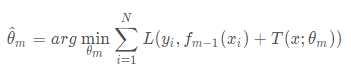
当采用平方误差损失函数时,
其损失变为
这里,
是当前模型拟合数据的残差(residual)。所以,对回归问题的提升树算法来说,只需简单地拟合当前模型的残差。