变分法是最优控制问题的三大基石之一,下面讨论一些变分法的常用理论。
无约束最优控制问题,若固定起止时间,两端状态固定,即
x
(
0
)
=
x
0
,
x
(
t
f
)
=
x
f
,
t
∈
[
0
,
t
f
]
x(0)=x_0, x(t_f)=x_f, t\in[0,t_f]
x ( 0 ) = x 0 , x ( t f ) = x f , t ∈ [ 0 , t f ]
x
∗
(
t
)
x^*(t)
x ∗ ( t )
min
x
(
t
)
J
(
x
,
t
)
=
ϕ
(
x
(
t
f
)
,
t
f
)
+
∫
0
t
f
L
(
x
,
x
˙
,
t
)
d
t
(1)
\min_{x(t)}J(x,t)=\phi(x(t_f),t_f)+\int_0^{t_f}L(x,\dot{x} ,t)\text d t \tag{1}
x ( t ) min J ( x , t ) = ϕ ( x ( t f ) , t f ) + ∫ 0 t f L ( x , x ˙ , t ) d t ( 1 )
X
\Chi
X
R
\Reals
R
T
:
X
↦
R
T: \Chi\mapsto\Reals
T : X ↦ R
x
(
t
)
↦
J
∈
R
x(t)\mapsto J\in\Reals
x ( t ) ↦ J ∈ R
(
1
)
(1)
( 1 )
J
(
x
,
t
)
=
∫
0
t
f
d
ϕ
(
x
,
t
)
d
t
+
L
(
x
,
x
˙
,
t
)
d
t
+
ϕ
(
x
(
0
)
,
0
)
J(x,t)=\int_0^{t_f}\frac{\text d\phi(x,t)}{\text d t}+L(x,\dot{x} ,t)\text d t+\phi(x(0),0)
J ( x , t ) = ∫ 0 t f d t d ϕ ( x , t ) + L ( x , x ˙ , t ) d t + ϕ ( x ( 0 ) , 0 )
对于上述问题,沿着最优路径
x
∗
(
t
)
x^*(t)
x ∗ ( t )
δ
J
(
x
∗
)
\delta J(x^*)
δ J ( x ∗ )
δ
J
(
x
∗
)
=
0
\delta J(x^*)=0
δ J ( x ∗ ) = 0
δ
J
(
δ
x
∗
)
=
∫
0
t
f
(
∂
L
∂
x
δ
x
+
∂
L
∂
x
˙
δ
x
˙
)
d
t
=
0
\delta J(\delta x^*) =\int_0^{t_f}({\frac {\partial L}{\partial x}\delta x}+ {\frac {\partial L}{\partial \dot x}\delta \dot x)\text d t}=0
δ J ( δ x ∗ ) = ∫ 0 t f ( ∂ x ∂ L δ x + ∂ x ˙ ∂ L δ x ˙ ) d t = 0
u
v
=
∫
d
(
u
v
)
=
u
∫
d
v
+
v
∫
d
u
uv=\int \text d (uv)=u\int \text d v+v\int \text d u
u v = ∫ d ( u v ) = u ∫ d v + v ∫ d u
∫
L
x
˙
δ
x
˙
d
t
=
∫
L
x
˙
δ
d
x
d
t
d
t
=
∫
L
x
˙
δ
d
x
=
L
x
˙
δ
x
−
∫
δ
x
d
L
x
˙
=
L
x
˙
δ
x
−
∫
δ
x
d
L
x
˙
d
t
d
t
\int L_{\dot{x}} \delta \dot x \text d t=\int L_{\dot{x}} \delta \frac{\text d x}{\text d t}\text d t=\int L_{\dot{x}} \delta \text d x=L_{\dot{x}}\delta x-\int{\delta x}\text d L_{\dot x}=L_{\dot{x}}\delta x-\int{\delta x}\frac{\text d L_{\dot x}}{\text d t}\text d t
∫ L x ˙ δ x ˙ d t = ∫ L x ˙ δ d t d x d t = ∫ L x ˙ δ d x = L x ˙ δ x − ∫ δ x d L x ˙ = L x ˙ δ x − ∫ δ x d t d L x ˙ d t
L
x
˙
δ
x
∣
0
t
f
+
∫
0
t
f
(
L
x
−
d
d
t
L
x
˙
)
δ
x
d
t
=
0
(2)
{\left. L_{\dot{x}}\delta x \right|}_0^{t_f}+\int_0^{t_f}(L_x-\frac{\text d}{\text d t}L_{\dot x}\text )\delta xd t=0\tag{2}
L x ˙ δ x ∣ 0 t f + ∫ 0 t f ( L x − d t d L x ˙ ) δ x d t = 0 ( 2 )
L
x
˙
(
x
(
t
f
)
,
x
˙
(
t
f
)
,
t
f
)
⋅
δ
x
(
t
f
)
−
L
x
˙
(
x
0
,
x
˙
0
,
0
)
⋅
δ
x
0
=
0
[
L
x
(
x
(
t
)
,
x
˙
(
t
)
,
t
)
−
d
d
t
L
x
˙
(
x
(
t
)
,
x
˙
(
t
)
,
t
)
]
⋅
δ
x
=
0
\begin{aligned} L_{\dot x}(x(t_f),\dot x(t_f),t_f)\cdot\delta x(t_f)-L_{\dot x}(x_0,\dot x_0,0)\cdot\delta x_0=0\\ [L_x(x(t),\dot x(t),t)-\frac{\text d}{\text d t}L_{\dot x}(x(t),\dot x (t),t)\text ]\cdot\delta x=0 \end{aligned}
L x ˙ ( x ( t f ) , x ˙ ( t f ) , t f ) ⋅ δ x ( t f ) − L x ˙ ( x 0 , x ˙ 0 , 0 ) ⋅ δ x 0 = 0 [ L x ( x ( t ) , x ˙ ( t ) , t ) − d t d L x ˙ ( x ( t ) , x ˙ ( t ) , t ) ] ⋅ δ x = 0
δ
x
(
t
)
\delta x(t)
δ x ( t )
δ
x
(
t
0
)
=
0
\delta x(t_0)=0
δ x ( t 0 ) = 0
L
x
−
d
d
t
L
x
˙
=
0
(3)
L_x-\frac{\text d}{\text d t}L_{\dot x}=0\tag 3
L x − d t d L x ˙ = 0 ( 3 )
L
x
˙
(
x
f
)
=
0
L_{\dot{x}}(x_f)=0
L x ˙ ( x f ) = 0
t
f
t_f
t f
x
(
t
f
)
x(t_f)
x ( t f )
x
f
∈
X
f
≠
∅
x_f\in X_f\neq \emptyset
x f ∈ X f = ∅
x
(
t
)
x(t)
x ( t )
t
f
t_f
t f
x
f
x_f
x f 边界条件
x
(
0
)
,
t
f
,
x
(
t
f
)
x(0),t_f,x(t_f)
x ( 0 ) , t f , x ( t f )
(
3
)
(3)
( 3 ) 百度百科-最速下降曲线问题 ,该问题为约翰伯努利提出,被欧拉解决。例1.1 求无约束最优化问题的最优路径
J
(
x
)
=
∫
0
π
/
2
[
x
˙
2
(
t
)
−
x
2
(
t
)
]
d
t
x
(
0
)
=
0
,
x
(
π
/
2
)
=
1
J(x)=\int_{0}^{\pi / 2}\left[\dot{x}^{2}(t)-x^{2}(t)\right] d t\\ x(0)=0,x(\pi/2)=1
J ( x ) = ∫ 0 π / 2 [ x ˙ 2 ( t ) − x 2 ( t ) ] d t x ( 0 ) = 0 , x ( π / 2 ) = 1
0
=
∂
L
∂
x
(
x
∗
(
t
)
,
x
˙
∗
(
t
)
,
t
)
−
d
d
t
[
∂
L
∂
x
˙
(
x
∗
(
t
)
,
x
˙
∗
(
t
)
,
t
)
]
=
−
2
x
∗
(
t
)
−
d
d
t
[
2
x
˙
∗
(
t
)
]
\begin{aligned} 0 &=\frac{\partial L}{\partial x}\left(x^{*}(t), \dot{x}^{*}(t), t\right)-\frac{d}{d t}\left[\frac{\partial L}{\partial \dot{x}}\left(x^{*}(t), \dot{x}^{*}(t), t\right)\right] \\ &=-2 x^{*}(t)-\frac{d}{d t}\left[2 \dot{x}^{*}(t)\right]\\ \end{aligned}
0 = ∂ x ∂ L ( x ∗ ( t ) , x ˙ ∗ ( t ) , t ) − d t d [ ∂ x ˙ ∂ L ( x ∗ ( t ) , x ˙ ∗ ( t ) , t ) ] = − 2 x ∗ ( t ) − d t d [ 2 x ˙ ∗ ( t ) ]
x
(
t
)
+
x
′
′
(
t
)
=
0
x(t)+x''(t)=0
x ( t ) + x ′ ′ ( t ) = 0
x
(
t
)
=
a
e
ı
(
t
+
ϕ
)
,
(
ı
2
=
−
1
)
x(t)=ae^{\imath (t+\phi)},(\imath^2=-1)
x ( t ) = a e ı ( t + ϕ ) , ( ı 2 = − 1 )
a
=
1
,
ϕ
=
−
π
/
2
;
&
a
=
−
1
,
ϕ
=
π
/
2
a=1,\phi=-\pi/2;\& a=-1,\phi=\pi/2
a = 1 , ϕ = − π / 2 ; & a = − 1 , ϕ = π / 2
x
(
t
)
=
s
i
n
(
t
)
x(t)=sin(t)
x ( t ) = s i n ( t )
t
f
t_f
t f
x
f
x_f
x f 必要条件为Euler方程——公式
(
3
)
(3)
( 3 )
L
x
˙
(
x
f
)
=
0
L_{\dot{x}}(x_f)=0
L x ˙ ( x f ) = 0
t
f
t_f
t f
x
f
x_f
x f
t
f
t_f
t f
x
f
x_f
x f
(
3
)
(3)
( 3 )
L
x
˙
(
x
f
)
=
0
L
(
x
,
x
˙
,
t
f
)
=
0
(4)
\begin{aligned} L_{\dot{x}}(x_f)=0\\ L(x,\dot x ,t_f)=0\tag{4} \end{aligned}
L x ˙ ( x f ) = 0 L ( x , x ˙ , t f ) = 0 ( 4 )
t
f
t_f
t f
x
f
x_f
x f 两者之间的关系为
ψ
i
(
x
f
,
t
f
)
=
0
,
i
=
1
,
2
,
.
.
.
m
,
(
m
<
n
)
\psi_i(x_f,t_f)=0,i=1,2,...m, (m<n)
ψ i ( x f , t f ) = 0 , i = 1 , 2 , . . . m , ( m < n )
x
x
x
μ
∈
R
m
×
1
\mu\in\Reals^{m\times1}
μ ∈ R m × 1
J
(
x
,
t
)
=
μ
T
ψ
+
∫
0
t
f
L
d
t
=
∫
0
t
f
L
+
μ
T
d
ψ
d
t
d
t
J(x,t)=\mu^T\psi+\int_0^{t_f}L\text d t=\int_0^{t_f}L+\mu^T\frac{\text d \psi}{\text d t}\text d t
J ( x , t ) = μ T ψ + ∫ 0 t f L d t = ∫ 0 t f L + μ T d t d ψ d t
H
(
x
,
μ
)
=
L
+
μ
T
d
ψ
d
t
(5)
H(x,\mu)=L+\mu^T\frac{\text d \psi}{\text d t}\tag{5}
H ( x , μ ) = L + μ T d t d ψ ( 5 )
H
x
−
d
d
t
H
x
˙
=
0
(6)
H_x-\frac{\text d}{\text d t}H_{\dot x}=0\tag 6
H x − d t d H x ˙ = 0 ( 6 )
(
4
)
(4)
( 4 )
H
x
˙
(
x
f
)
=
0
H
(
x
,
x
˙
,
t
f
)
=
0
(7)
\begin{aligned} H_{\dot{x}}(x_f)=0\\ H(x,\dot x ,t_f)=0\tag 7 \end{aligned}
H x ˙ ( x f ) = 0 H ( x , x ˙ , t f ) = 0 ( 7 )
L
x
˙
+
μ
T
∂
ψ
∂
x
T
=
0
L
+
μ
T
d
ψ
d
t
=
0
(8)
\begin{aligned} L_{\dot{x}}+\mu^T\frac{\partial \psi}{\partial x^T}=0\\ L+\mu^T\frac{\text d \psi}{\text d t}=0 \tag{8} \end{aligned}
L x ˙ + μ T ∂ x T ∂ ψ = 0 L + μ T d t d ψ = 0 ( 8 )
(
8
)
(8)
( 8 )
(
x
f
,
t
f
)
(x_f ,t_f)
( x f , t f )
μ
\mu
μ
例1.2 求椭圆外一点
(
x
0
,
y
0
)
(x_0,y_0)
( x 0 , y 0 )
x
2
8
+
y
2
4
=
1
\frac{x^2} 8+\frac {y^2} 4=1
8 x 2 + 4 y 2 = 1
y
(
x
)
y(x)
y ( x )
这里考虑到还没有引入状态过程约束,所以不假设最短路径是直线PQ,而是广义的形式
y
(
x
)
y(x)
y ( x )
d
s
=
d
x
2
+
d
y
2
=
1
+
y
′
2
d
x
\text d s=\sqrt{\text d x^2+\text d y^2}=\sqrt{1+y\prime^2}\text d x
d s = d x 2 + d y 2
= 1 + y ′ 2
d x
y
(
x
)
y(x)
y ( x )
J
(
y
(
x
)
,
x
)
=
∫
x
0
x
f
1
+
y
′
2
d
x
J(y(x),x)=\int_{x_0}^{x_f}\sqrt{1+y\prime^2}\text d x
J ( y ( x ) , x ) = ∫ x 0 x f 1 + y ′ 2
d x
y
(
x
0
)
=
y
0
y(x_0)=y_0
y ( x 0 ) = y 0
x
f
x_f
x f
y
(
x
f
)
y(x_f)
y ( x f )
ψ
(
y
(
x
f
)
,
x
f
)
=
x
2
+
2
y
2
−
8
=
0
\psi(y(x_f),x_f)=x^2+2y^2-8=0
ψ ( y ( x f ) , x f ) = x 2 + 2 y 2 − 8 = 0
(
5
)
−
(
8
)
(5)-(8)
( 5 ) − ( 8 )
H
(
y
(
x
)
,
x
)
=
L
+
μ
d
ψ
d
x
=
1
+
y
′
2
+
μ
(
2
x
+
4
y
y
′
)
H(y(x),x)=L+\mu\frac{\text d\psi}{\text d x}=\sqrt{1+y\prime^2}+\mu(2x+4y y^\prime)
H ( y ( x ) , x ) = L + μ d x d ψ = 1 + y ′ 2
+ μ ( 2 x + 4 y y ′ )
H
y
−
d
d
x
H
y
˙
=
4
μ
y
′
−
d
d
x
(
y
′
1
+
y
′
2
+
4
μ
y
)
=
−
y
′
′
(
1
+
y
′
2
)
3
/
2
=
0
H_y-\frac{\text d}{\text d x}H_{\dot y}=4\mu y^\prime-\frac{\text d}{\text d x}(\frac{y'}{\sqrt{1+y\prime^2}}+4\mu y)=-\frac {y''}{(1+y'^2)^{3/2}}=0
H y − d x d H y ˙ = 4 μ y ′ − d x d ( 1 + y ′ 2
y ′ + 4 μ y ) = − ( 1 + y ′ 2 ) 3 / 2 y ′ ′ = 0
y
′
=
a
y'=a
y ′ = a
y
(
x
)
y(x)
y ( x )
y
0
=
a
x
0
+
b
y
f
=
a
x
f
+
b
x
f
2
+
2
y
f
2
−
8
=
0
1
+
a
2
+
μ
(
2
x
f
+
4
y
f
a
)
=
0
a
1
+
a
2
+
4
μ
y
f
=
0
\begin{aligned} y_0=a x_0+b\\ y_f=a x_f+b\\ x_f^2+2y_f^2-8=0\\ \sqrt{1+a^2}+\mu(2 x_f+4y_f a)=0\\ \frac a{\sqrt{1+a^2}}+4\mu y_f=0 \end{aligned}
y 0 = a x 0 + b y f = a x f + b x f 2 + 2 y f 2 − 8 = 0 1 + a 2
+ μ ( 2 x f + 4 y f a ) = 0 1 + a 2
a + 4 μ y f = 0
(
x
0
,
y
0
)
=
(
2
,
0
)
=
F
2
(x_0,y_0)=(2,0)=F_2
( x 0 , y 0 ) = ( 2 , 0 ) = F 2
a
=
b
=
0
,
y
f
=
0
,
x
f
=
2
2
,
μ
=
1
/
(
8
−
12
2
)
a=b=0,y_f=0,x_f=2\sqrt 2,\mu=1/(8-12\sqrt 2)
a = b = 0 , y f = 0 , x f = 2 2
, μ = 1 / ( 8 − 1 2 2
)
上面对待终端约束,我们应用了Lagrange乘数
μ
\mu
μ 例1.1 中我们处理的,虽然知道是直线但还是用了曲线假设;为了处理最优路径问题中的约束,我们引入Lagrange乘子
λ
\lambda
λ
也称为几何约束
g
i
(
x
(
t
)
,
t
)
=
0
,
i
=
1
,
2
,
.
.
.
m
,
(
m
≤
n
)
g_i(x(t),t)=0,i=1,2,...m,(m\le n)
g i ( x ( t ) , t ) = 0 , i = 1 , 2 , . . . m , ( m ≤ n )
λ
(
t
)
∈
R
m
×
1
\lambda(t)\in\Reals^{m\times1}
λ ( t ) ∈ R m × 1
J
(
x
,
λ
,
t
)
=
∫
0
t
f
L
+
λ
T
g
d
t
=
∫
0
t
f
H
(
x
,
λ
,
t
)
d
t
(9)
J(x,\lambda,t)=\int_0^{t_f}L+\lambda^Tg \text d t=\int_0^{t_f}H(x,\lambda,t)\text d t\tag 9
J ( x , λ , t ) = ∫ 0 t f L + λ T g d t = ∫ 0 t f H ( x , λ , t ) d t ( 9 )
这里考虑一阶常微分方程形式的动态约束:
f
(
x
(
t
)
,
x
˙
(
t
)
,
t
)
=
0
f(x(t),\dot x(t),t)=0
f ( x ( t ) , x ˙ ( t ) , t ) = 0
t
f
t_f
t f
x
f
x_f
x f
λ
(
t
)
∈
R
m
×
1
\lambda(t)\in\Reals^{m\times1}
λ ( t ) ∈ R m × 1
J
(
x
,
x
˙
,
λ
,
t
)
=
∫
0
t
f
L
+
λ
T
f
d
t
=
∫
0
t
f
H
(
x
,
x
˙
,
λ
,
t
)
d
t
(10)
J(x,\dot x,\lambda,t)=\int_0^{t_f}L+\lambda^Tf \text d t=\int_0^{t_f}H(x,\dot x,\lambda,t)\text d t\tag {10}
J ( x , x ˙ , λ , t ) = ∫ 0 t f L + λ T f d t = ∫ 0 t f H ( x , x ˙ , λ , t ) d t ( 1 0 )
(
10
)
(10)
( 1 0 )
(
9
)
(9)
( 9 )
δ
x
(
t
)
˙
\delta \dot {x(t)}
δ x ( t ) ˙
δ
x
(
t
)
\delta x(t)
δ x ( t )
δ
λ
(
t
)
\delta \lambda(t)
δ λ ( t )
δ
J
(
δ
x
∗
,
δ
λ
∗
)
=
∫
t
0
t
f
{
[
L
x
+
λ
T
f
x
]
δ
x
(
t
)
+
[
L
x
˙
+
λ
T
f
x
]
δ
x
˙
(
t
)
+
δ
λ
T
(
t
)
f
}
d
t
=
∫
0
t
f
[
(
H
x
−
d
d
t
H
x
˙
)
δ
x
+
f
T
δ
λ
(
t
)
]
d
t
\delta J(\delta x^*,\delta \lambda^*) =\int_{t_{0}}^{t_{f}}\left\{\left[L_{\mathbf{x}}+\mathbf{\lambda}^{T} \mathbf{f}_{\mathbf{x}}\right] \delta \mathbf{x}(t)+\left[L_{\dot{\mathbf{x}}}+\mathbf{\lambda}^{T} \mathbf{f}_{\mathbf{x}}\right] \delta \dot{\mathbf{x}}(t)+\delta \lambda^T(t) f \right\} \text d t \\ =\int_0^{t_f}\big [(H_x-\frac{\text d}{\text d t}H_{\dot x})\delta \mathbf{x}+ \mathbf{f}^{T} \delta \mathbf{\lambda}(t)\big]\text dt
δ J ( δ x ∗ , δ λ ∗ ) = ∫ t 0 t f { [ L x + λ T f x ] δ x ( t ) + [ L x ˙ + λ T f x ] δ x ˙ ( t ) + δ λ T ( t ) f } d t = ∫ 0 t f [ ( H x − d t d H x ˙ ) δ x + f T δ λ ( t ) ] d t
H
x
−
d
d
t
H
x
˙
=
0
f
(
x
(
t
)
,
x
˙
(
t
)
,
t
)
=
0
(11)
\begin{aligned}H_x-\frac{\text d}{\text d t}H_{\dot x}=0\\ \mathbf f(\mathbf x(t),\dot \mathbf x(t),t)=0\tag{11} \end{aligned}
H x − d t d H x ˙ = 0 f ( x ( t ) , x ˙ ( t ) , t ) = 0 ( 1 1 )
函数L(x)取极值的必要条件是
∂
L
∂
x
=
0
\frac{\partial L}{\partial x}=0
∂ x ∂ L = 0
L
(
x
1
,
x
2
)
=
[
x
1
,
x
2
]
[
−
1
,
1
1
,
3
]
[
x
1
x
2
]
L(x_1,x_2)=\left[\begin{array}{l} x_1,x_2\end{array}\right]\left[\begin{array}{r} -1,1 \\1,3 \end{array}\right]\left[\begin{array}{l} x_1\\x_2 \end{array}\right]
L ( x 1 , x 2 ) = [ x 1 , x 2 ] [ − 1 , 1 1 , 3 ] [ x 1 x 2 ]
∂
L
∂
x
=
[
−
1
,
1
1
,
3
]
[
0
0
]
=
[
0
0
]
\frac{\partial L}{\partial x}=\begin{bmatrix}-1,1\\1,3 \end{bmatrix} \begin{bmatrix}0\\0 \end{bmatrix} =\begin{bmatrix}0\\0 \end{bmatrix}
∂ x ∂ L = [ − 1 , 1 1 , 3 ] [ 0 0 ] = [ 0 0 ]
x
1
<
0
,
x
2
=
0
x_1<0,x_2=0
x 1 < 0 , x 2 = 0
∂
2
L
∂
u
2
⋟
0
\frac{\partial^{2} L}{\partial u^{2}}\curlyeqsucc0
∂ u 2 ∂ 2 L ⋟ 0
对于泛函极值问题,若有以下性能指标
min
x
(
t
)
J
(
x
,
t
)
=
∫
0
t
f
L
(
x
,
x
˙
,
t
)
d
t
\min_{x(t)}J(x,t)=\int_0^{t_f}L(x,\dot{x} ,t)\text d t
x ( t ) min J ( x , t ) = ∫ 0 t f L ( x , x ˙ , t ) d t
(
3
)
(3)
( 3 )
∂
2
L
∂
x
˙
2
⋟
0
(12)
\frac{\partial^{2} L}{\partial \dot x^{2}}\curlyeqsucc0\tag{12}
∂ x ˙ 2 ∂ 2 L ⋟ 0 ( 1 2 )
前面的最优路径都假设极值曲线
x
∗
(
t
)
x^*(t)
x ∗ ( t ) 连续但不是处处可导 的,而是在某些角点出现:
x
(
t
1
−
)
=
x
(
t
1
+
)
;
x
˙
(
t
1
−
)
≠
x
˙
(
t
1
+
)
x(t_1^-)=x(t_1^+); \dot x(t_1^-)\neq\dot x(t_1^+)
x ( t 1 − ) = x ( t 1 + ) ; x ˙ ( t 1 − ) = x ˙ ( t 1 + )
L
x
−
d
d
t
L
x
˙
=
0
,
t
∈
[
0
,
t
1
)
⋃
(
t
1
,
t
f
]
L_x-\frac{\text d}{\text d t}L_{\dot x}=0,t\in[0,t_1)\bigcup(t_1,t_f]
L x − d t d L x ˙ = 0 , t ∈ [ 0 , t 1 ) ⋃ ( t 1 , t f ]
L
x
˙
(
t
1
−
)
=
L
x
˙
(
t
1
+
)
L
(
t
1
−
)
−
x
˙
T
L
x
˙
(
t
1
−
)
=
L
(
t
1
+
)
−
x
˙
T
L
x
˙
(
t
1
+
)
(13)
\begin{aligned} L_{\dot x}(t_1^-)&=L_{\dot x}(t_1^+)\\ L(t_1^-)-\dot\mathbf x^TL_{\dot x}(t_1^-)&=L(t_1^+)-\dot\mathbf x^TL_{\dot x}(t_1^+) \tag{13} \end{aligned}
L x ˙ ( t 1 − ) L ( t 1 − ) − x ˙ T L x ˙ ( t 1 − ) = L x ˙ ( t 1 + ) = L ( t 1 + ) − x ˙ T L x ˙ ( t 1 + ) ( 1 3 )
[1] 邢继祥. 最优控制应用基础[M]. 科学出版社, 2003.


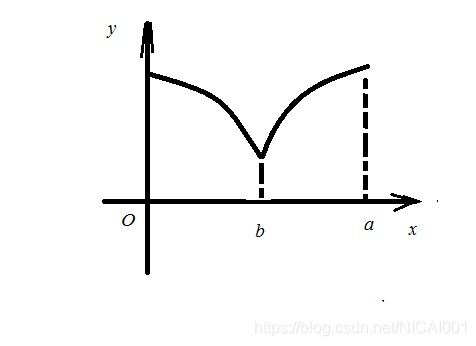 由于极值曲线分段可导,则分段满足Euler方程,
由于极值曲线分段可导,则分段满足Euler方程,