楔子
numpy中有一个einsum方法,也就是我们说的"爱因斯坦求和",它具有非常强大的表达能力。像矩阵的"点积"、"外积"、"转置"等等都可以使用"爱因斯坦求和"实现,并且会更加方便,但是缺点就是它的符号代表的含义需要花点时间才能理解。下面我们就来看看怎么使用:
注意:爱因斯坦求和用好了会很方便,并且很酷。但如果不用爱因斯坦求和,我们也完全可以使用numpy的其它方法实现。
爱因斯坦求和最大的亮点,就是它可以只使用几个符号就能表达丰富的含义,但是不使用它也是完全没问题的,并且这种方法能不用就尽量不要用。比如矩阵的转置,直接arr.T即可,像这种就没有必要使用爱因斯坦求和。
最后就是效率问题,爱因斯坦求和的效率在有些场景其实不是那么优秀的,后面我们会专门进行测试,看看它和其它方法实现起来在效率上会有什么差别。其实,爱因斯坦求和比较适合装(a+c)/2
爱因斯坦中的符号
首先numpy的einsum函数接收一个字符串(英文字符组成,即:符号)和任意多个数组,传递的数组的个数要和符号匹配。下面我们来看看这个符号到底是什么?
我们都知道数组有维度的概念,比如一个数组可以是一维、二维、三维等等,我们使用英文字符来表示对应的维度,怎么理解呢?比如一个数组有三维,那么我们就用三个英文字符来表示。但是三个英文字符分别代表哪一个维度呢,很简单,直接将英文字符进行升序排序,然后对应数组的维度。
比如:aMi,排完序之后是Mai,那么M代表第一个维度、a代表第二个维度,i代表第三个维度。
但是注意的是,虽然排完序对应的维度是固定的,但是aMi和aiM两个符号代表的含义是不一样的,这一点在演示代码的时候很容易看出来。
我们来代码实际演示一下:
import numpy as np
arr = np.array([1, 2, 3, 4])
# 这个数组是一维的,那么只需要一个英文字符即可。
# einsum中的符号只需要一个英文字符
arr_view = np.einsum("a", arr)
print(arr_view) # [1 2 3 4]
"""
这个会返回arr的一个视图,在视图上做修改会影响原来的数组
"""
arr_view[0] = 111
print(arr) # [111 2 3 4]
# 另外我们说可以是任意的英文字符,而目前的arr只有一个维度
# 那么我们输入任意的英文字符都是可以的
print(np.einsum("k", arr)) # [111 2 3 4]
print(np.einsum("P", arr)) # [111 2 3 4]
print(np.einsum("T", arr)) # [111 2 3 4]
print(np.einsum("v", arr)) # [111 2 3 4]
print(np.einsum("q", arr)) # [111 2 3 4]
如果你是第一次接触einsum,那么目前或许会有点懵,但是不要紧,正常现象。我们慢慢往下看,最后你一定会理解的。
我们使用二维数组演示一下
import numpy as np
arr = np.array([[1, 2, 3, 4]])
# 这个数组是二维的,那么需要两个英文字符。
print(np.einsum("ij", arr)) # [[1 2 3 4]]
"""
依旧返回arr的视图,我们在视图上进行修改会影响原来的数组本身
"""
# 我们说符号的英文字符是任意的,只是个数要和数组的维度进行匹配
# 我们这里的arr是二维的,那么符号里面的英文字符个数也要是两个,但是字符是什么英文字符则没有要求
print(np.einsum("av", arr)) # [[1 2 3 4]]
try:
print(np.einsum("abc", arr))
except Exception as e:
"""
这里就报错了,因为我们指定符号为"abc",三个字符
但是数组只有两个维度,于是不匹配,所以报错
"""
print(e) # einstein sum subscripts string contains too many subscripts for operand 0
# 我们虽然说,英文字符个数只要对应就行,但是英文字符是什么则没有要求
# 但是排列之后的顺序还是要对应的
print(np.einsum("sm", arr))
"""
[[1]
[2]
[3]
[4]]
"""
# 注意此时就变了,我们说"sm"和"ms"是不一样的,尽管它们都是m对应第一维、s对应第二维,因为排完序m在前s在后
# 原来数组的shape是(1, 4), m对应1,s对应4
# 但是符号如果是"sm",那么新返回的视图的shape变成(4, 1)。等于将数组转置了
所以ab、bc、xy、av这几个符号代表的含义是一样的,因为它们排序之后还是原来的顺序。
比如:数组的shape是(2, 3),那么它们得到的数组的shape还是(2, 3)
但如果符号是sm就不同了,s代表第二维,m代表第一维,所以sm等于将数组的shape变成(3, 2)
但是注意:sm将shape从(2, 3)变成(3, 2)并不是reshape成(3, 2),而是进行了转置
我们对比一下区别:
import numpy as np
arr = np.arange(0, 12).reshape((3, 4))
print(arr)
"""
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
"""
# reshape成(4, 3)
print(arr.reshape((4, 3)))
"""
[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
[ 9 10 11]]
"""
# 等价于转置
print(np.einsum("sm", arr))
"""
[[ 0 4 8]
[ 1 5 9]
[ 2 6 10]
[ 3 7 11]]
"""
# 因为转置之后,如果原来的shape为(a, b),那么会变成(b, a)
# 所以np.einsum("sm", arr)是将数组进行了转置
# 而reshape和转置是不一样的
所以我们目前使用爱因斯坦求和实现了转置的操作,那么它和直接使用转置之间的效率如何呢?
import numpy as np
arr = np.arange(0, 12).reshape((3, 4))
print(arr)
"""
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
"""
print(arr.T)
"""
[[ 0 4 8]
[ 1 5 9]
[ 2 6 10]
[ 3 7 11]]
"""
print(np.einsum("ba", arr))
"""
[[ 0 4 8]
[ 1 5 9]
[ 2 6 10]
[ 3 7 11]]
"""
我们注意到:这两个返回的结果都是一样的,那么我们来看看效率上的差别,下面我们在jupyter notebook上测试
>>> %timeit arr.T
122 ns ± 0.787 ns per loop
>>> %timeit np.einsum("ba", arr)
1.26 µs ± 91.3 ns per loop
1µs = 1000ns,所以我们看到使用爱因斯坦求和进行转至是没有arr.T快的,可以说慢了10倍。
另外,爱因斯坦求和进行转置、arr.T、以及reshape本质上都只是创建了一个视图(view),在视图上修改是会影响原来的数组的。
单个数组
通过上面的例子,相信各位对爱因斯坦求和应该有个大致的印象了,下面我们来看看它的其它操作。
我们知道对于一个二维数组,如果符号为"ab",那么会获取原来数组的view,如果是"ba",虽然获取的还是view,但是shape会改变,对于二维数组则相当于转置。
但是,如果我们指定为"aa"呢?
import numpy as np
arr = np.arange(0, 12).reshape((3, 4))
print(arr)
"""
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
"""
try:
print(np.einsum("aa", arr))
except Exception as e:
print(e) # dimensions in operand 0 for collapsing index 'a' don't match (3 != 4)
"""
我们看到报错了,我们知道a代表第一个维度,所以相当于reshape成(3, 3),但是维度不匹配
其实不是这样的,如果是两个字符都一样的话,那么相当于求主对角线的和,因此它要求必须是方阵
"""
arr = np.arange(0, 16).reshape((4, 4))
print(arr)
"""
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]
[12 13 14 15]]
"""
# 需要arr是一个方阵,主对角线:0 5 10 15,所以加在一起是30
print(np.einsum("aa", arr)) # 30
# 求主对角线的和等价于np.trace,另外主对角线的和也叫作该矩阵的"迹"
print(np.trace(arr)) # 30
说到求和,爱因斯坦求和也是支持的,毕竟名字本身就包含了求和
求和
求和在爱因斯坦求和的符号中使用->表示
import numpy as np
arr = np.array([1, 2, 3, 4])
# 表示对返回的视图里面的元素进行求和
print(np.einsum("k->", arr), np.sum(arr)) # 10 10
但是我们看到上面的那个"aa"并没有包含->啊,求主对角线的和我们用的是"aa",事实上,aa和aa->是一样的。
import numpy as np
arr = np.arange(0, 16).reshape((4, 4))
print(np.einsum("kk", arr)) # 30
print(np.einsum("kk->", arr)) # 30
然后老规矩,我们看看二维数组,好好感受一波。
import numpy as np
arr = np.arange(0, 12).reshape((3, 4))
print(arr)
"""
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
"""
print(np.einsum("ij->", arr), np.sum(arr)) # 66 66
# 我们看到对二维数组求和也是没有问题的,但是对于np.sum可以指定坐标轴
print(np.sum(arr, axis=0)) # [12 15 18 21]
print(np.sum(arr, axis=1)) # [ 6 22 38]
# 那么,对于爱因斯坦求和可不可以指定呢?答案是可以的
# 我们来看看怎么用
print(np.einsum("ij->i", arr)) # [ 6 22 38]
print(np.einsum("ij->j", arr)) # [12 15 18 21]
print(np.einsum("ji->i", arr)) # [12 15 18 21]
print(np.einsum("ji->j", arr)) # [ 6 22 38]
估计有人会郁闷,到底是沿着哪一个轴进行相加,不知道该怎么判断。当然如果你很清楚axis=0和axis=1之间的区别的话,那么你会很容易明白。
这个地方如何理解,有多种方式,这里介绍一种我个人理解的方式。首先我们只看->的右边,我们说i表示第一个维度,j代表第二个维度,而原来的数组的shape是(3, 4)。如果是->i,那么代表和第一个维度的数组长度保持一致,->j则表示和第二个维度的数组长度保持一致。
ij对应(3, 4),因此ij->i的话,那么加完之后数组的长度应该为3;而ij->j的话,那么加完之后数组的长度应该为4。
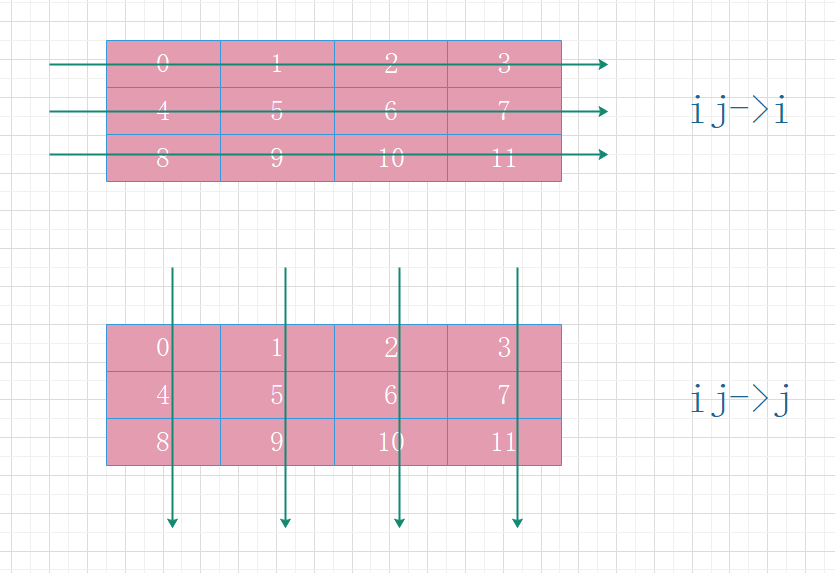
至于ji->i和ji->j,首先->右边的i和j代表的含义和上面一样,但是ji则是相当于将原来的数组转置了。原来数组的shape是(3, 4),那么转置完之后是(4, 3),所以ji->i,加完之后长度应该为4,因为第一个维度的数组长度变成了4,ji->j,加完之后长度应该为3。

相信此时你应该很对一个数组求和很清楚了,那么我们再看一下怎么获取主对角线
import numpy as np
arr = np.arange(0, 16).reshape((4, 4))
print(arr)
"""
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]
[12 13 14 15]]
"""
print(np.einsum("aa", arr)) # 30
print(np.einsum("aa->", arr)) # 30
# 我们说aa和aa->都是获取主对角线的和
# 而aa->a则是获取主对角线
print(np.einsum("aa->a", arr)) # [ 0 5 10 15]
"""
注意:我们这里的符号故意和之前写的不一样,因为aa->a、ii->i、BB->B都是一样的
"""
# 获取主对角线等价于
print(np.diag(arr)) # [ 0 5 10 15]
最后我们再比对一下效率问题:
>>> %timeit np.sum(arr)
3.27 µs ± 417 ns per loop
>>> %timeit np.einsum("ab", arr)
1.23 µs ± 38.5 ns per loop
>>> %timeit np.sum(arr, axis=0)
3.09 µs ± 10.9 ns per loop
>>> %timeit np.einsum("ab->b", arr) # ab->b等价于ij->j
1.72 µs ± 13.6 ns per loop
>>> %timeit np.sum(arr, axis=1)
3.97 µs ± 21.2 ns per loop
>>> %timeit np.einsum("ab->a", arr) # ab->a等价于ij->i
1.81 µs ± 74.6 ns per loop
可以看到,对于求和来说,爱因斯坦求和是有不小的优势的。
总结
对于单个数组来说,它的操作我们来总结一下。

两个一维数组
下面我们来看看两个数组之间怎么操作,我们上面是先介绍的einsum的符号,然后探究与之等价的其它方法。
现在我们先看两个数组之间有哪些操作,然后看怎么用einsum表达。
但是在此之前我们有一些概念需要了解。
向量的内积、外积和叉积
内积也叫作点积,两个向量如果想进行内积,那么这两个向量的分量个数必须相等。然后将对应位置的分量进行相乘,再整体求合,所以向量点积得到的结果是一个标量。
假设存在两个向量α和β,其中\(α = [a_{1}, a_{2}, ..., a_{n}]\),\(β = [b_{1}, b_{2}, ..., b_{n}]\),
那么向量α和β进行点积的结果就是\(a_{1} * b_{1} + a_{2} * b_{2} + ... + a_{n} * b_{n}\),
import numpy as np
arr1 = np.array([1, 2, 3])
arr2 = np.array([4, 5, 6])
# numpy中求两个向量的点积可以使用inner方法
print(np.inner(arr1, arr2)) # 32
向量的外积,看个公式和栗子就明白了
假设存在两个向量α和β,其中\(α = [a_{1}, a_{2}, ..., a_{m}]\),\(β = [b_{1}, b_{2}, ..., b_{n}]\),
那么向量α和β进行进行外积的结果就是:
\(\begin{bmatrix}a_{1}*b_{1},a_{1}*b_{2},...,a_{1}*b_{n}\\a_{2}*b_{1},a_{2}*b_{2},...,a_{2}*b_{n}\\a_{3}*b_{1},a_{3}*b_{2},...,a_{3}*b_{n}\\a_{m}*b_{1},a_{m}*b_{2},...,a_{m}*b_{n}\end{bmatrix}\)
import numpy as np
arr1 = np.array([2, 3, 4])
arr2 = np.array([3, 3, 3])
print(np.outer(arr1, arr2))
"""
[[ 6 6 6]
[ 9 9 9]
[12 12 12]]
"""
arr1 = np.array([2, 3, 4, 5, 6])
arr2 = np.array([3, 3, 3])
print(np.outer(arr1, arr2))
"""
[[ 6 6 6]
[ 9 9 9]
[12 12 12]
[15 15 15]
[18 18 18]]
"""
arr1 = np.array([2])
arr2 = np.array([3, 3, 3])
print(np.outer(arr1, arr2))
"""
[[6 6 6]]
"""
arr1 = np.array([2, 3, 4])
arr2 = np.array([3])
print(np.outer(arr1, arr2))
"""
[[ 6]
[ 9]
[12]]
"""
# 我们看到两个向量进行外积的话,不要求两个向量的分量个数相等
# 并且两个向量进行外积得到的是一个二维数组,也就是矩阵
# 在numpy中,我们把一维数组称之为向量,二维数组称之为矩阵。
向量的叉积,同样要求两个向量的分量个数必须一样。
假设存在两个向量α和β,其中\(α = [a_{1}, a_{2}, ..., a_{n}]\),\(β = [b_{1}, b_{2}, ..., b_{n}]\),
那么向量α和向量β进行叉积的结果就是下面
\(\begin{bmatrix}1 ,1,1,...,1\\a_{1},a_{2},a_{3},...,a_{n}\\b_{1},b_{2},b_{3},...,b_{n}\end{bmatrix}\)
这个矩阵的第一行的每个元素的代数余子式组成的向量。
import numpy as np
arr1 = np.array([2, 3, 4])
arr2 = np.array([4, 5, 3])
print(np.cross(arr1, arr2))
"""
[-11 10 -2]
"""
# 我们来看看是怎么计算的
# 我们说结果就是下面
"""
1, 1, 1
2, 3, 4
4, 5, 3
"""
# 这个矩阵的第一行的每个元素的代数余子式组成的向量
# 如果不知道代数余子式是什么,可以去百度一下,这里不提了
# 3 * 3 - 5 * 4, -1 * (2 * 3 - 4 * 4), 2 * 5 - 3 * 4
# 所以结果是(-11, 10, -2)
矩阵的相乘和点乘
下面解释一下矩阵的相乘和点乘,相乘就是对应位置的元素直接相乘即可;而点乘则是矩阵间的运算,如果两个矩阵A和B,想要进行A点乘B,那么需要满足A的列数等于B的行数,然后运算得到矩阵的行数等于矩阵A的行数、列数等于矩阵B的列数。
import numpy as np
arr1 = np.array([[1, 2, 3], [2, 3, 4]])
arr2 = np.array([[3, 1, 2], [2, 5, 1]])
print(arr1)
"""
[[1 2 3]
[2 3 4]]
"""
print(arr2)
"""
[[3 1 2]
[2 5 1]]
"""
print(arr1 * arr2)
"""
[[ 3 2 6]
[ 4 15 4]]
"""
# 说白了相乘就是对应位置的元素进行相乘
# 当然向量也是可以进行相乘的,如果相乘完了再把所有的元素相加就等价于两个向量的内积
# 而向量间的点乘,在python中使用@表示
try:
print(arr1 @ arr2)
except Exception:
print("error occurred") # error occurred
所以矩阵之间相乘是很好理解的,就是对应位置的元素相乘。但是点乘不一样,点乘就是要求第一个矩阵的列数等于第二个矩阵的行数。arr1和arr2的shape都是(2, 3),所以arr1的列数为3,arr2的行数为2,它们不相等,所以报错了
import numpy as np
arr1 = np.array([[1, 2, 3], [2, 3, 4]])
arr2 = np.array([[3, 1], [2, 5], [1, 3]])
print(arr1)
"""
[[1 2 3]
[2 3 4]]
"""
print(arr2)
"""
[[3 1]
[2 5]
[1 3]]
"""
try:
print(arr1 * arr2)
except Exception:
# 我们说相乘是对应位置的元素进行相乘,但是这两个矩阵的形状不一样
# 元素无法一一对应,所以报错了
print("error occurred") # error occurred
print(arr1 @ arr2)
"""
[[10 20]
[16 29]]
"""
# 但是点乘可以,点乘就是arr1的每一行和arr2的每一列进行内积
# 所以才要arr1的列数和arr2的行数相同,只有这样arr1的一行才可以arr2的一列进行内积
"""
arr1:
[[1 2 3]
[2 3 4]]
arr2:
[[3 1]
[2 5]
[1 3]]
arr1 @ arr2:
[[1 * 3 + 2 * 2 + 3 * 1, 1 * 1 + 2 * 5 + 3 * 3]
[2 * 3 + 3 * 2 + 4 * 1, 2 * 1 + 3 * 5 + 4 * 3]]
==>
[[10, 20]
[16, 29]]
"""
使用爱因斯坦求和
使用einsum对两个一维数组相乘
import numpy as np
arr1 = np.array([1, 2, 3])
arr2 = np.array([3, 4, 5])
print(arr1 * arr2) # [ 3 8 15]
"""
两个数组相乘,就是将里面的对应元素相乘
如果再将所有元素相加就是内积
"""
# 我们看到此时有两个数组,所以"->"的左侧出现了用于分隔的逗号
print(np.einsum("i,i->i", arr1, arr2)) # [ 3 8 15]
使用einsum对两个一维数组内积
import numpy as np
arr1 = np.array([1, 2, 3])
arr2 = np.array([3, 4, 5])
print(np.inner(arr1, arr2)) # 26
"""
就是矩阵内的对应元素彼此相乘,然后再将所有元素加在一起
1 * 3 + 2 * 4 + 3 * 5 = 26
"""
print(np.einsum("i,i->", arr1, arr2)) # 26
使用einsum对两个一维数组外积
import numpy as np
arr1 = np.array([1, 2, 3])
arr2 = np.array([3, 4, 5])
print(np.outer(arr1, arr2))
"""
[[ 3 4 5]
[ 6 8 10]
[ 9 12 15]]
"""
print(np.einsum("i,j->ij", arr1, arr2))
"""
[[ 3 4 5]
[ 6 8 10]
[ 9 12 15]]
"""
估计这里可能有人会懵,我们来解释一下。首先两个一维数组,那么它们的符号都只能是一个英文字符,然后使用逗号分割。如果是i,i->i,那么表示两个向量里面的元素进行相乘,乘完之后的元素个数和原来一样。
如果是i,i->,那么很好理解,则是乘完之后就相加。
最后是i,j->ij,可能有点难理解。我们说单个二维数组ij,那么等于返回一个视图。但如果类似i,j,是两个数组,那么就表示两个数组相乘,至于怎么相乘,则取决于符号本身。而i,j->ij表示进行外积,因为->ij表示要返回一个二维数组,shape为(i, j)。
import numpy as np
arr1 = np.array([1, 2, 3])
arr2 = np.array([3, 4, 5])
print(np.outer(arr1, arr2))
"""
[[ 3 4 5]
[ 6 8 10]
[ 9 12 15]]
"""
print(np.sum(np.outer(arr1, arr2))) # 72
print(np.einsum("i,j->", arr1, arr2)) # 72
"""
i,j->ij: 返回一个shape为(i, j)的二维数组
i,j->: 返回一个shape为(i, j)的二维数组的所有元素的和
i,i->i: 返回一个shape为(i,)的一维数组
i,i->: 返回一个shape为(i,)的一维数组的所有元素的和
"""
然后来看个稍微拐个弯的
import numpy as np
arr1 = np.array([1, 2, 3])
arr2 = np.array([3, 4, 5])
print(np.outer(arr1, arr2))
"""
[[ 3 4 5]
[ 6 8 10]
[ 9 12 15]]
"""
print(np.einsum("i,j->i", arr1, arr2)) # [12 24 36]
print(np.einsum("i,j->j", arr1, arr2)) # [18 24 30]
"""
我们说i,j可以看成是一个二维数组,shape为(i, j)
如果是i,j->ij,那么就返回这个shape为(i, j)的二维数组
如果是i,j->,那么就返回这个shape为(i, j)的二维数组的所有元素的和
但如果是i,j->i的话,显然是在某一个方向上进行求和。至于在哪一个方向,可以看我们上面说的单个二维数据的求和
"""
print(np.einsum("j,i->i", arr1, arr2)) # [18 24 30]
print(np.einsum("j,i->j", arr1, arr2)) # [12 24 36]
"""
我们说i,j可以看成是返回一个shape为(i, j)的二维数组,而j,i则还是可以看成是返回一个shape为(i, j)的二维数组
所以结果是相反的
"""
# 仔细感受一下下面几个式子的不同
print(np.einsum("i,j->ij", arr1, arr2))
"""
[[ 3 4 5]
[ 6 8 10]
[ 9 12 15]]
"""
print(np.einsum("i,j->ji", arr1, arr2))
"""
[[ 3 6 9]
[ 4 8 12]
[ 5 10 15]]
"""
print(np.einsum("j,i->ji", arr1, arr2))
"""
[[ 3 4 5]
[ 6 8 10]
[ 9 12 15]]
"""
print(np.einsum("j,i->ij", arr1, arr2))
"""
[[ 3 6 9]
[ 4 8 12]
[ 5 10 15]]
"""
# i,j->ij:arr1的长度为i,arr2的长度为j,返回的数组shape为(i, j)
# j,i->ji:arr1的长度为j,arr2的长度为i,返回的数组shape为(j, i)
# 所以i,j->ij和j,i->ji是一样的
# 但是如果是->i或者->j,需要对某一方向进行求和,那么无论是i,j->i还是j,i->,默认返回的都是二维数组的shape都是(i,j)
两个二维数组
这里介绍两个二维数组之间的爱因斯坦求和,关于一维数组和二维数组之间由于涉及到广播运算,我们就不说了
实现两个矩阵的相乘
import numpy as np
arr1 = np.array([[1, 2, 3], [2, 3, 4]])
arr2 = np.array([[3, 4, 5], [5, 1, 2]])
print(arr1)
"""
[[1 2 3]
[2 3 4]]
"""
print(arr2)
"""
[[3 4 5]
[5 1 2]]
"""
print(arr1 * arr2)
"""
[[ 3 8 15]
[10 3 8]]
"""
print(np.einsum("ij,ij->ij", arr1, arr2))
"""
[[ 3 8 15]
[10 3 8]]
"""
# 我们说两个一维数组、也就是向量相乘是"i,i->i",表示两个向量对应元素相乘,返回shape为(i,)的向量
# 而矩阵相乘,则是"ij,ij->ij",表示两个矩阵对应位置的元素相乘,返回shape为(i,j)的矩阵
# 所以如果想对应位置的元素相乘,那么就用相同的符号表示就可以了
# 同理"ij,ji->ij"表示arr1和arr2的转置进行相乘,当然这里会报错,因为arr2转置之后和arr1就不能一一对应了
实现两个矩阵的点乘
import numpy as np
arr1 = np.array([[1, 2, 3], [2, 3, 4]])
arr2 = np.array([[3, 1], [2, 5], [1, 3]])
print(arr1)
"""
[[1 2 3]
[2 3 4]]
"""
print(arr2)
"""
[[3 1]
[2 5]
[1 3]]
"""
print(arr1 @ arr2)
"""
[[10 20]
[16 29]]
"""
# 点乘,arr1的每一行要和arr2的每一列内积,最终计算之后的矩阵的行数为arr1的行数,列数为arr2的列数
# 并且arr1的第二个维度要和arr2的第一个维度的数组长度一致
# 所以"ij,jk->ik",
print(np.einsum("ij,jk->ik", arr1, arr2))
"""
[[10 20]
[16 29]]
"""
带上转置
import numpy as np
arr1 = np.array([[1, 2, 3], [2, 3, 4]])
arr2 = np.array([[3, 4, 5], [5, 1, 2]])
# 我们说arr1和arr2之间可以相乘,但是无法点乘
# 但如果将arr2转置一下不就可以了吗?
print(np.einsum("ij,kj->ik", arr1, arr2))
"""
[[26 13]
[38 21]]
"""
print(arr1 @ arr2.T)
"""
[[26 13]
[38 21]]
"""
# "ij,kj",因为j是第一个维度、k是第二个维度,所以"ij,kj->ik"表示将arr1和转置之后的arr2进行点乘
import numpy as np
arr1 = np.array([[1, 2, 3], [2, 3, 4]])
arr2 = np.array([[3, 1], [2, 5], [1, 3]])
print(arr1 * arr2.T)
print(np.einsum("ij,ji->ij", arr1, arr2))
"""
[[ 3 4 3]
[ 2 15 12]]
"""
# "ij,ij->ij"表示对应元素相乘
# "ij,ji->ij"表示将arr2转置之后,再和arr1对应元素相乘
总结
我个人觉得这个爱因斯坦算法确实有点太难理解了,个人建议没事的话还是不要乱用,其实用普通的numpy的方法完全可以轻松的实现。目前介绍的算是比较浅显的了,更复杂的用法可以参考官网。