Автор: Ю Фань
фон
Развитие искусственного интеллекта (ИИ) открыло новую парадигму научных открытий. Сегодня ИИ начал улучшать, ускорять и обеспечивать наше понимание природных явлений в широком диапазоне пространственных и временных масштабов, тем самым способствуя развитию естествознания и создавая новую область исследований AI4Science. Недавно в обзорной статье «Искусственный интеллект для науки в квантовых, атомистических и континуальных системах», написанной совместно более чем 60 авторами, представлен углубленный технический обзор в подобластях субатомных, атомных и континуальных систем. Здесь мы извлекаем техническую основу этого обзора и сосредоточиваемся на том, как построить эквивариантную модель при преобразовании симметрии.
1. Введение
В 1929 году квантовый физик Поль Дирак отмечал: «Фундаментальные физические законы, необходимые для математической теории большей части физики и всей химии, нам уже полностью известны, и трудность заключается в том, что точное применение этих законов приводит к комплекс. Это справедливо от уравнения Шредингера в квантовой физике до уравнения Навье-Стокса в механике жидкости. Глубокое обучение может ускорить решение этих уравнений. Используя результаты традиционных методов моделирования в качестве обучающих данных, после обучения эти модели могут делать прогнозы намного быстрее, чем традиционное моделирование.
В других областях, таких как биология, лежащие в основе биофизические процессы могут быть не полностью поняты и в конечном итоге не могут быть описаны математическими уравнениями. В этих случаях модели глубокого обучения можно обучать с использованием экспериментально сгенерированных данных, таких как модели прогнозирования белков AlphaFold, RoseTTAFold, ESMFold и других 3D-структур, полученных в ходе экспериментов, так что точность предсказанных вычислительными методами 3D-структур белков может быть сопоставима с экспериментальными результатами. .
1.1 Научные области
Научные области, представляющие интерес в этой статье, организованы в виде обзора на рисунке ниже в соответствии с пространственными и временными масштабами моделируемой физической системы.
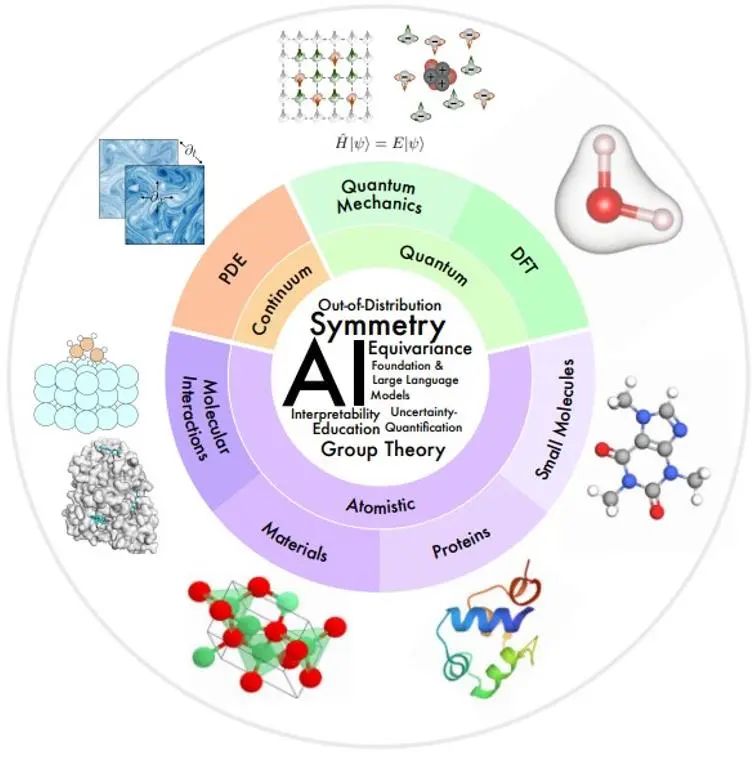
Малый масштаб: Квантовая механика использует волновую функцию для изучения физических явлений в наименьшем масштабе. Уравнение Шредингера, которому она подчиняется, описывает полный динамический процесс квантовой системы, но оно приводит к экспоненциальной сложности. Теория функционала плотности (DFT) и методы квантовой химии ab initio представляют собой методы первых принципов, широко используемые на практике для расчета электронной структуры и физических свойств молекул и материалов, а также могут дополнительно определять электронные и механические свойства молекул и твердых тел, оптические. , магнитные и каталитические свойства. Однако эти методы по-прежнему являются дорогостоящими в вычислительном отношении, что ограничивает их использование небольшими системами (~ 1000 атомов). Модель искусственного интеллекта может помочь повысить скорость и точность.
Мезомасштаб: небольшие молекулы, обычно размером от десятков до сотен атомов, играют важную регуляторную и сигнальную роль во многих химических и биологических процессах. Белки — это большие молекулы, состоящие из одной или нескольких цепей аминокислот. Последовательность аминокислот определяет структуру белков, которая, в свою очередь, определяет их функцию. Исследования в области материаловедения изучают взаимосвязь между обработкой, структурой, свойствами и материалами. Молекулярные взаимодействия изучают, сколько физических и биологических функций выполняются посредством молекулярных взаимодействий, таких как взаимодействия лиганд-рецептор и взаимодействие молекула-материал. В этих областях ИИ добился большого прогресса в молекулярной характеристике и создании, молекулярной динамике, прогнозировании и проектировании структуры белков, прогнозировании свойств материалов и создании структур.
Большой масштаб: механика сплошной среды использует уравнения в частных производных для моделирования физических процессов, которые развиваются во времени и пространстве на макроскопическом уровне, включая поток жидкости, теплопередачу, электромагнитные волны и т. д. Методы искусственного интеллекта обеспечивают некоторые решения таких проблем, как повышение эффективности вычислений, обобщение и анализ с несколькими разрешениями.
1.2 Область технологий искусственного интеллекта
Во многих областях научного ИИ существует общий набор технических проблем.
**Симметрия.**Симметрия — это очень сильная индуктивная паранойя, поэтому ключевой задачей AI4Science является то, как эффективно интегрировать симметрию в модели ИИ.
**Интерпретируемость:**Интерпретируемость имеет решающее значение в AI4Science для понимания законов физического мира.
**Обобщение и причинно-следственная связь вне распределения (OOD): **Чтобы избежать создания обучающих данных для каждого отдельного параметра, необходимо определить причинные факторы, которые делают возможным обобщение OOD.
**Базовые модели и большие языковые модели:**Базовые модели для задач обработки естественного языка предварительно обучаются под самоконтролируемым или обобщаемым контролем для выполнения различных последующих задач с помощью нескольких или нулевых шагов. В статье представлен взгляд на то, как эта парадигма может ускорить открытия AI4Science.
**Количественная оценка неопределенности (UQ): **Изучает, как обеспечить надежное принятие решений в условиях неопределенности данных и модели.
**Образование.** Чтобы облегчить обучение и образование, в этой статье представлен категоризированный список ресурсов, которые автор считает полезными, а также представлены взгляды на то, как сообщество может лучше способствовать интеграции ИИ с наукой и образованием.
**2. ** Симметрия, эквивариантность и их теории.
Во многих научных задачах интересующий объект обычно расположен в трехмерном пространстве, и любое математическое представление объекта опирается на опорную систему координат, создавая такое представление относительно системы координат. Однако системы координат не существуют в природе, поэтому необходимо представление, независимое от системы координат. Поэтому одна из ключевых задач AI4Science — как добиться инвариантности или эквивариантности при преобразовании системы координат.
2.1 Обзор
Симметрия означает тот факт, что свойства физического явления остаются неизменными при определенных преобразованиях, например преобразованиях координат. Если в системе существуют определенные симметрии, цель прогнозирования естественным образом инвариантна или эквивариантна относительно соответствующего преобразования симметрии. Например, при прогнозировании энергии трехмерной молекулы прогнозируемое значение остается неизменным при перемещении или вращении трехмерной молекулы. Альтернативной стратегией обучения с учетом симметрии является использование увеличения данных в контролируемом обучении, в частности применение случайных преобразований симметрии к входным данным и меткам, чтобы заставить модель выводить приблизительно эквивариантные прогнозы. Но у этого есть много недостатков:
1) Учитывая дополнительные степени свободы в выборе системы координат, модель требует большей мощности для представления изначально простых закономерностей в фиксированной системе координат;
2) Многие преобразования симметрии, такие как трансляция, могут создавать бесконечное количество эквивариантных выборок, что затрудняет ограниченное улучшение данных для полного отражения симметрии в данных;
3) В некоторых случаях необходимо построить очень глубокую модель для достижения хороших результатов прогнозирования. Если каждый уровень модели не может поддерживать эквивариантность, будет сложно предсказать общий результат эквивариантности;
4) В научных задачах, таких как молекулярное моделирование, крайне важно обеспечить прогноз, устойчивый к преобразованиям симметрии, чтобы машинное обучение можно было использовать надежным образом.
Из-за множества недостатков увеличения данных все больше и больше исследований сосредотачиваются на разработке моделей машинного обучения, отвечающих требованиям симметрии. В рамках архитектуры адаптации симметрии модель может сосредоточиться на задаче прогнозирования цели обучения без улучшения данных.
2.2 Эквивариантность при дискретном преобразовании симметрии
В этом разделе автор приводит пример сохранения эквивариантности при дискретных преобразованиях симметрии в модели ИИ. Этот пример задачи имитирует отображение скалярного поля потока в двумерной плоскости от одного момента к другому. Когда поле входного потока поворачивается на 90, 180 и 270 градусов, поле выходного потока также будет вращаться соответственно. Его математическое выражение выглядит следующим образом:
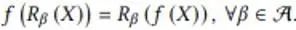
где f представляет собой функцию отображения поля потока, а R представляет преобразование дискретного вращения. Коэн и др. предложили эквивариантные групповые сверточные нейронные сети (G-CNN) для решения этой проблемы. Его простейшим базовым компонентом является восходящая свертка:
1) Сначала поверните ядро свертки на все углы в симметричном преобразовании и используйте повернутое ядро свертки для выполнения соответствующих операций свертки на входе, чтобы получить несколько слоев объектов, и сложите эти слои объектов в вновь созданное измерение вращения α Вместе 2; ) Объединение выполняется в этом измерении вращения α, так что результирующий выход будет производить соответствующее вращение при вращении входа X.
Из-за существования операции объединения, хотя эквивариантные строки сохраняются, эти функции не могут нести информацию о направлении. Обычно G-CNN принимают структуру, как показано на следующем рисунке:
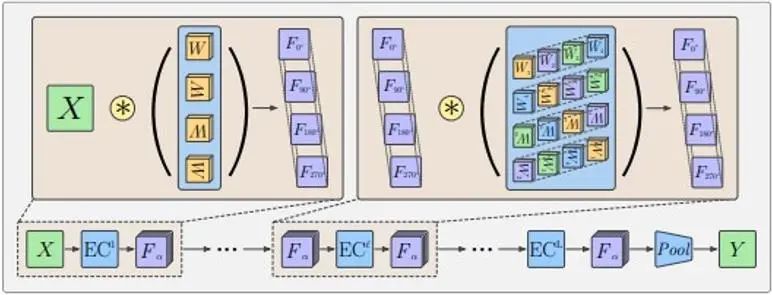
Сначала используется ядро вращательной свертки для увеличения размерности входных данных, затем используется многослойный групповой слой свертки, чтобы каждый слой признаков соответствовал требованиям вращательной эквивалентности при сохранении вращательной размерности, и, наконец, слой объединения используется для устранения вращательного размера. Это позволяет промежуточному слою объектов лучше обнаруживать закономерности в относительном положении и ориентации объектов. Смысл эквивалентности промежуточного векторного слоя заключается в том, что векторный слой вращается соответствующим образом при преобразовании вращения, а также вращается порядок в измерении вращения, а также вращается и конструкция вращения ядра свертки в используемом слое групповой свертки; выходные данные Слой объектов может поддерживать эту характеристику эквивалентности.
2.3-2.5 Построение эквивариантной модели непрерывного 3D преобразования
Во многих научных задачах мы фокусируемся на непрерывной симметрии вращения и перемещения в трехмерном пространстве. Например, когда структура химических молекул вращается и перемещается, вектор, состоящий из предсказанных молекулярных атрибутов, претерпевает соответствующие преобразования. Эти преобразования непрерывного вращения R и преобразования перемещения t составляют элементы группы SE(3), и эти преобразования могут быть выражены как матрицы преобразования в векторном пространстве. Матрицы преобразования в разных векторных пространствах могут быть разными, но эти векторные пространства можно разложить на независимые подвекторные пространства. В каждом подпространстве действуют одни и те же правила преобразования, то есть вектор, полученный применением всех элементов преобразования в группе к вектору подпространства, все еще находится в подпространстве. Следовательно, элементы преобразования в группе могут быть неприводимыми в подпространстве. Матричное представление подпространства. Например, такие скаляры, как полная энергия и энергетическая щель, остаются неизменными под действием элементов группы SE(3), а их матрица преобразования выражается как D^0(R)=1 под элементами группы SE(3); Трехмерные векторы, такие как силовые поля. Соответствующее вращение происходит под действием, и его матрица преобразования выражается как D^1(R)=R в векторном пространстве более высокой размерности, D^l(R) представляет собой 2l+1; -мерная квадратная матрица. Эти матрицы преобразования D^l(R) называются матрицей Вигнера-D l-порядка, соответствующей вращению R, а соответствующее субвекторное пространство становится неприводимым инвариантным подпространством l-порядка группы SE(3), а Вектор в нем называется l Порядково-эквивариантным вектором. При трансляционном преобразовании эти векторы всегда остаются неизменными, поскольку свойства, которые нас интересуют, связаны только с относительным положением.
Обычный способ сопоставить трехмерную геометрическую информацию с объектами в инвариантном подпространстве группы SE(3) — использовать отображение сферических гармонических функций. Функция сферической гармоники Y^l отображает трехмерный вектор в 2l+1-мерный вектор, который представляет собой коэффициент при разложении входного вектора на 2l+1 базовую сферическую гармоническую функцию. Как показано на рисунке ниже, поскольку используется только ограниченное количество оснований, дельта-функция на сфере, представленной трехмерным вектором, будет в определенной степени расширена.

Сферические гармоники обладают следующими эквивариантными свойствами:
Среди них D — упомянутая ранее матрица Вигнера-D l-порядка. Таким образом, пространственная функция разлагается на комбинацию эквивариантных векторов разных порядков при преобразовании вращения.
Предполагая, что в нейронной сети графа с атомными координатами в качестве узлов признак узла h является эквивариантным вектором порядка l_1, тогда следующая передача и обновление информации графа может гарантировать, что обновленный h также поддерживает эквивариантность:
Ключевым шагом в этом является операция тензорного произведения (TP) во время передачи информации. Среди них vec означает векторизацию матрицы, а коэффициент C представляет собой матрицу с 2l_3+1 строками (2l_1+1) (2l_2+1) столбцами.
Узловой признак h является вектором в неприводимом инвариантном подпространстве порядка l_1. Сферическая гармоническая функция Y направления ребра r_ij является вектором в неприводимом инвариантном подпространстве порядка l_2. Вектор, полученный прямым произведением этих двух векторов. пространство приводимо, а коэффициент C представляет собой отношение преобразования этого приводимого пространства в неприводимое инвариантное подпространство порядка l_3. Например, пространство прямого произведения двух трехмерных векторов выглядит следующим образом:
Матрицу преобразования вращения пространства прямого произведения можно преобразовать в трехблочную диагональную матрицу в середине рисунка выше, что означает, что это пространство можно разложить на три неприводимых инвариантных подпространства с размерностями 1, 3 и 5. то есть 3⨂ Разложение векторного пространства 3=1⊕3⊕5. Коэффициент C представляет собой матрицу преобразования этого девятимерного пространства в одномерное, трехмерное и пятимерное пространства соответственно. В приведенной выше формуле l_1, l_2 и l_3 принимают только одно значение и являются эквивариантными признаками фиксированного порядка. Объекты в реальной сети могут представлять собой комбинацию этих объектов разного порядка.
2.6-2.7 В предыдущих примерах использовалась теория групп и свойства сферических гармонических функций. Базовые знания теории групп и сферических гармонических функций подробно представлены в этих двух главах статьи.
2.8 Управляемое ядро представляет собой общую форму эквивариантной сети.
Предыдущие эквивариантные слои сети при дискретных и непрерывных преобразованиях можно описать в виде единой переменной свертки (управляемой CNN):
Среди них x и y — это пространственные координаты, f_in(y) представляет собой входной вектор объектов в координате y, f_out(x) представляет собой выходной вектор объектов в координате x, а K — преобразование из входного пространства объектов в выходной объект. космос. Операция свертки обеспечивает трансляционную эквивалентность. Чтобы гарантировать эквивалентность при других пространственных аффинных преобразованиях, ядро свертки K также должно удовлетворять следующим ограничениям симметрии:
Среди них g — преобразование в группе пространственных преобразований, а ρ_in и ρ_out представляют представление преобразования во входном и выходном пространствах признаков (т. е. матрице преобразования) соответственно.
На этом этапе теоретическое объяснение симметрии и эквивариантности в статье практически подошло к концу, после чего следует отдельный обзор многочисленных полей, перечисленных в главе 1.
Рекомендации
[1] Рен П., Рао С., Лю Ю и др. PhyCRNet: сверточно-рекуррентная сеть с учетом физики для решения пространственно-временных уравнений в уравнениях [J]. Компьютерные методы в прикладной механике и технике, 2022, 389:114399.
[2] https://www.sciencedirect.com/science/article/abs/pii/S0045782521006514?via%3Dihub
【1】 Сюань Чжан, Лимей Ван, Джейкоб Хельвиг и др. 2023. Искусственный интеллект для науки в квантовых, атомистических и континуальных системах. arXiv: https://arxiv.org/abs/2307.08423
【2】 Тако Коэн и Макс Веллинг. 2016. Групповые эквивариантные сверточные сети. На Международной конференции по машинному обучению. ПМЛР, 48:2990–2999.
【3】 Натаниэль Томас, Тесс Смидт, Стивен Кирнс и др. 2018. Тензорные полевые сети: нейронные сети, эквивариантные по вращению и перемещению для трехмерных облаков точек. arXiv: https://arxiv.org/abs/1802.08219
Морис Вейлер, Марио Гейгер, Макс Веллинг и др. 2018. 3D-управляемые CNN: изучение вращательно-эквивариантных функций в объемных данных. В достижениях в области нейронных систем обработки информации
Программист, родившийся в 1990-х годах, разработал программу для переноса видео и заработал более 7 миллионов менее чем за год. Концовка была очень суровой! Google подтвердил увольнения, связанные с «проклятием 35-летней давности» китайских программистов в командах Flutter, Dart и . Python Arc Browser для Windows 1.0 через 3 месяца официально Доля рынка Windows 10 достигает 70%, Windows 11 GitHub продолжает снижаться GitHub выпускает собственный инструмент разработки AI GitHub Copilot Workspace JAVA. — единственный запрос строгого типа, который может обрабатывать OLTP+OLAP. Это лучший ORM. Мы встречаемся слишком поздно.