[TSP] Решение TSP, основанное на алгоритме роя частиц Matlab Hopfield [включая исходный код Matlab 224]

1. Введение

1 Нейронная сеть Хопфилда
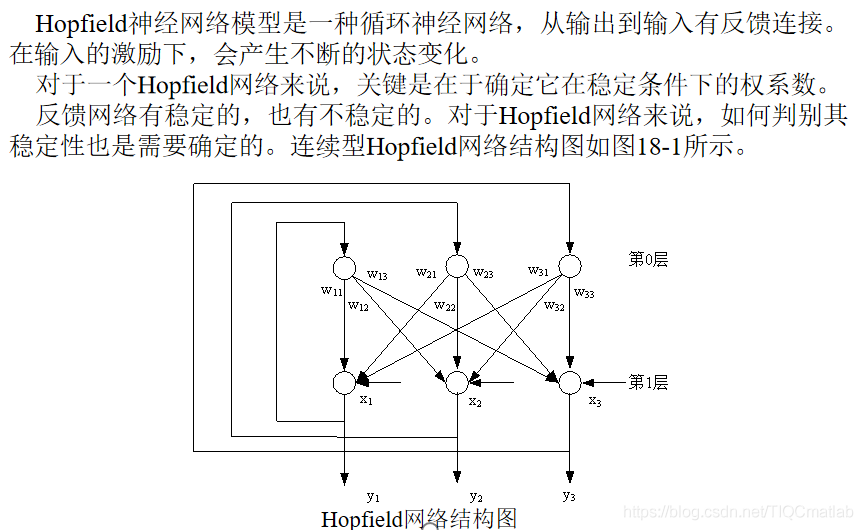
Вставьте описание изображения сюда
2 Дискретная сеть Хопфилда

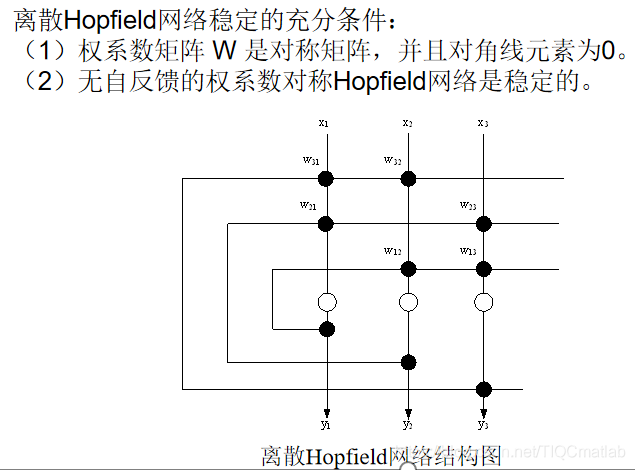
3 Непрерывная сеть Хопфилда

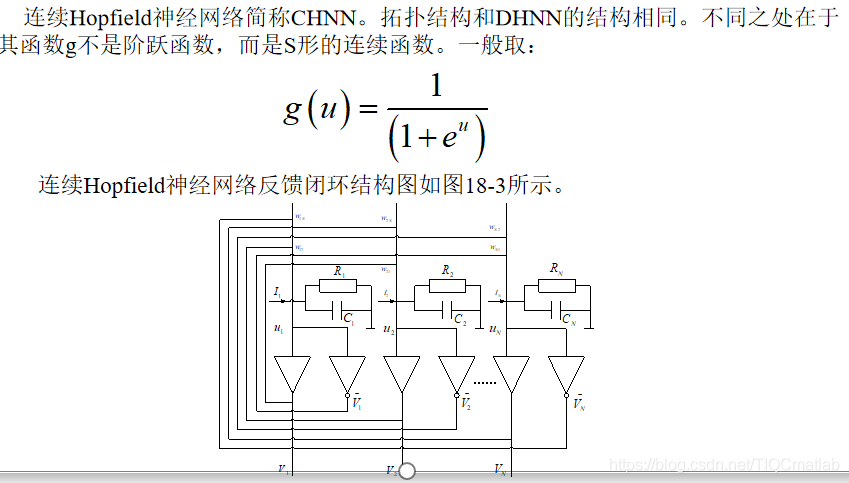
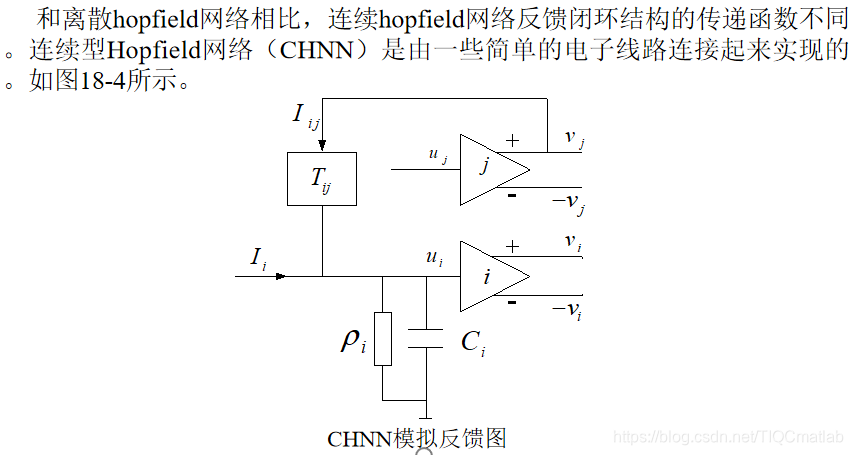
CHNN описывается нелинейными дифференциальными уравнениями.Стабильность сети описывается путем построения ее энергетической функции (также известной как функция Ляпунова), и с использованием вторых теорем Ляпунова об устойчивости делаются заключения.
Пояснение:
(1) функция Ляпунова не уникальна;
(2) если функция Ляпунова сети не может быть найдена, сеть не может быть доказана как нестабильная;
(3) в настоящее время не существует единого метода функции поиска Ляпунова;
(4 ) Использование метода энергетической функции для исследования устойчивости сети не является математически строгим.
Если целевая функция задачи оптимизации преобразована в функцию энергии сети, а переменные задачи соответствуют состоянию сети, то нейронная сеть Хопфилда может быть использована для решения задачи комбинации оптимизации.
Общие шаги по применению нейронной сети Хопфилда для решения задач оптимизационного расчета:
(1) Проанализировать проблему: выход сети соответствует решению задачи;
(2) Построить функцию энергии сети: сделать минимальное значение, соответствующее наилучшему решение проблемы;
(3) проектирование структуры сети: проектирование параметров сети из энергетической функции и условий устойчивости сети для получения динамического уравнения;
(4) программное моделирование MATLAB.

Во-вторых, исходный код

%% 连续Hopfield神经网络的优化—旅行商问题优化计算
% function main
%% 清空环境变量、定义全局变量
clc % 清屏
clear all; % 删除workplace变量
close all; % 关掉显示图形窗口
global A D
%% 导入城市位置
load city_location
%% 计算相互城市间距离
distance=dist(citys,citys');
%% 初始化网络
N=size(citys,1);
A=200;
D=100;
U0=0.1;
step=0.0001;
delta=2*rand(N,N)-1;
U=U0*log(N-1)+delta;
V=(1+tansig(U/U0))/2;
iter_num=10000;
E=zeros(1,iter_num);
%% 寻优迭代
for k=1:iter_num  
    % 动态方程计算
    dU=diff_u(V,distance);
    % 输入神经元状态更新
    U=U+dU*step;
    % 输出神经元状态更新
    V=(1+tansig(U/U0))/2;
    % 能量函数计算
    e=energy(V,distance);
    E(k)=e;  
end
 %% 判断路径有效性
[rows,cols]=size(V);
V1=zeros(rows,cols);
[V_max,V_ind]=max(V);
for j=1:cols
    V1(V_ind(j),j)=1;
end
C=sum(V1,1);
R=sum(V1,2);
flag=isequal(C,ones(1,N)) & isequal(R',ones(1,N));
%% 结果显示
if flag==1
   % 计算初始路径长度
   sort_rand=randperm(N);
   citys_rand=citys(sort_rand,:);
   Length_init=dist(citys_rand(1,:),citys_rand(end,:)');
   for i=2:size(citys_rand,1)
       Length_init=Length_init+dist(citys_rand(i-1,:),citys_rand(i,:)');
   end
   % 绘制初始路径
   figure(1)
   plot([citys_rand(:,1);citys_rand(1,1)],[citys_rand(:,2);citys_rand(1,2)],'o-')
   for i=1:length(citys)
       text(citys(i,1),citys(i,2),['   ' num2str(i)])
   end
   text(citys_rand(1,1),citys_rand(1,2),['       起点' ])
   text(citys_rand(end,1),citys_rand(end,2),['       终点' ])
   title(['优化前路径(长度：' num2str(Length_init) ')'])
   axis([0 1 0 1])
   grid on
   xlabel('城市位置横坐标')
   ylabel('城市位置纵坐标')
   % 计算最优路径长度
   [V1_max,V1_ind]=max(V1);
   citys_end=citys(V1_ind,:);
   Length_end=dist(citys_end(1,:),citys_end(end,:)');
   for i=2:size(citys_end,1)
       Length_end=Length_end+dist(citys_end(i-1,:),citys_end(i,:)');
   end
   disp('最优路径矩阵');V1
   % 绘制最优路径
   figure(2)
   plot([citys_end(:,1);citys_end(1,1)],...
       [citys_end(:,2);citys_end(1,2)],'o-')
   for i=1:length(citys)
       text(citys(i,1),citys(i,2),['  ' num2str(i)])
   end
   text(citys_end(1,1),citys_end(1,2),['       起点' ])
   text(citys_end(end,1),citys_end(end,2),['       终点' ])
   title(['优化后路径(长度：' num2str(Length_end) ')'])
   axis([0 1 0 1])
   grid on
   xlabel('城市位置横坐标')
   ylabel('城市位置纵坐标')
   % 绘制能量函数变化曲线
   figure(3)
   plot(1:iter_num,E);
   ylim([0 2000])
   title(['能量函数变化曲线(最优能量：' num2str(E(end)) ')']);
   xlabel('迭代次数');
   ylabel('能量函数');
else
   disp('寻优路径无效');
end
%% 连续Hopfield神经网络的优化—旅行商问题优化计算
% function TSP_hopfield()
%% 清空环境变量、定义全局变量
clc % 清屏
clear all; % 删除workplace变量
close all; % 关掉显示图形窗口
% step 1
A=1.5;
D=1;
u0=0.02;
step=0.01;
% step 2
N=8;
DistanceCity=dist(citys,citys');
% step 3
u=2*rand(N,N)-1;
U=0.5*u0*log(N-1)+u;
V=(1+tanh(U/u0))/2;
end

Три, результаты бега

Вставьте описание изображения сюда

Четыре, примечания

Полный код или написание добавить QQ1564658423 прошлый обзор
>>>>>>
[модель прогнозирования] прогноз lssvm на основе роя частиц Matlab [включая исходный код 103 Matlab]
[прогноз lSSVM] на основе алгоритма оптимизации китов Matlab прогнозирование данных lSSVM [включая исходный код Matlab 104]
[прогноз lstm] Улучшенное прогнозирование lstm на основе алгоритма оптимизации кита Matlab [Включая исходный код Matlab 105]
[Предсказание SVM] Улучшенное прогнозирование SVM на основе алгоритма bat matlab (1) [Включая исходный код Matlab 106]
[ Прогнозирование SVM】 На основе алгоритм matlab серого волка для оптимизации прогнозирования векторной машины поддержки svm [включая исходный код 107 Matlab]
[модель прогнозирования] на основе прогнозирования нейронной сети Matlab BP [включая исходный код 108 Matlab]
[модель прогнозирования lssvm] на основе алгоритма летучих мышей улучшенный метод наименьших квадратов Вектор поддержки машинное предсказание lssvm [проблема Matlab 109]
[предсказание lssvm] Наименьшие квадраты поддерживают векторное машинное предсказание lssvm на основе алгоритма гашения моли улучшено [Matlab 110]
[предсказание SVM] Улучшено предсказание SVM на основе алгоритма bat Matlab (два) [Включить исходный код Matlab 141 период]