
1. Descrição
2. Introdução à biblioteca de métodos
Os métodos de Monte Carlo (MC) e de diferença temporal (TD) são técnicas fundamentais no campo da aprendizagem por reforço; eles resolvem problemas de previsão com base na experiência com o ambiente, e não em um modelo do ambiente. No entanto, os métodos TD são uma combinação de métodos MC e programação dinâmica (DP) e, portanto, diferem dos métodos MC em termos de regras de atualização, bootstrapping e viés/variância. Os métodos TD também comprovadamente apresentam melhor desempenho e convergência mais rápida do que MC na maioria dos casos.
Neste post comparamos os métodos TD(2) e α MC constante no ambiente de grade simples e no ambiente de passeio aleatório [0] mais abrangente. Esperamos que esta postagem ajude os leitores interessados em aprendizado por reforço a entender melhor como cada método atualiza a função de valor de estado e como eles funcionam de maneira diferente no mesmo ambiente de teste.
Implementaremos o algoritmo e comparação em Python, as bibliotecas utilizadas neste artigo são as seguintes:
python==3.9.16
numpy==1.24.3
matplotlib==3.7.13. A diferença entre TD e MC
3.1 Introduzir TD(0) e constante α MC
Um método α MC constante é um método MC regular com um parâmetro de tamanho de passo constante α, o que ajuda a tornar a estimativa do valor mais sensível à experiência recente. Na prática, a escolha do valor de α depende do compromisso entre estabilidade e adaptabilidade. A seguir está a fórmula para o método MC atualizar a função de valor do estado no tempo t:

TD(0) é um caso especial de TD(λ), que está apenas um passo à frente e é a forma mais simples de aprendizagem de TD. Este método atualiza a função valor-estado com o erro TD, que é a diferença entre a estimativa do estado e a recompensa mais a estimativa do próximo estado. O parâmetro de tamanho de passo constante α funciona da mesma maneira que o método MC acima. A seguir está a equação TD(0) para atualizar a função de valor de estado no tempo t:

Em geral, as diferenças entre os métodos MC e TD ocorrem de três maneiras:
- Regra de atualização: O método MC só atualiza o valor após o término do episódio; isso pode tornar o programa mais lento se o episódio for longo ou pode ser problemático em tarefas contínuas onde não há nenhum episódio. Em contraste, os métodos TD atualizam estimativas de valor a cada passo de tempo; isto é aprendizagem online, que é especialmente útil em tarefas contínuas.
- Bootstrapping: O termo “ bootstrapping ” na aprendizagem por reforço refere-se à atualização de uma estimativa de valor com base em outras estimativas de valor. A atualização do método TD(0) é baseada no valor do estado seguinte, portanto é um método bootstrap; em contrapartida, MC não utiliza bootstrap porque atualiza o valor diretamente do valor de retorno (G).
- Viés/variância : os métodos MC são imparciais porque estimam valores ponderando os retornos reais observados sem fazer estimativas durante os episódios; no entanto, os métodos MC apresentam alta variância, especialmente quando o tamanho da amostra é pequeno. Em contraste, os métodos TD são tendenciosos porque usam bootstrapping, e o viés pode variar com base na implementação real; os métodos TD têm menor variância porque usam recompensas imediatas mais uma estimativa do próximo estado, eliminando recompensas e flutuações de ações causadas pela aleatoriedade.
3.2 Avaliação de TD(0) e α MC constante em uma configuração mundial de grade simples
Para tornar suas diferenças mais diretas, podemos configurar um ambiente de teste Gridworld simples com duas trajetórias fixas, executar ambos os algoritmos na configuração até a convergência e verificar como eles atualizam os valores de forma diferente.
Primeiro, podemos configurar o ambiente de teste com o seguinte código:
# Environment setup
def get_env():
grid = np.zeros(shape=(6, 6), dtype=float)
grid[:, -1] = -1
grid[2, -1] = 1
return grid
# Pre-defined paths
def get_paths():
path_1 = [(4, 0), (4, 1), (3, 1), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5)]
path_2 = [(5, 3), (4, 3), (3, 3), (2, 3), (1, 3), (0, 3), (0, 4), (0, 5)]
return path_1, path_2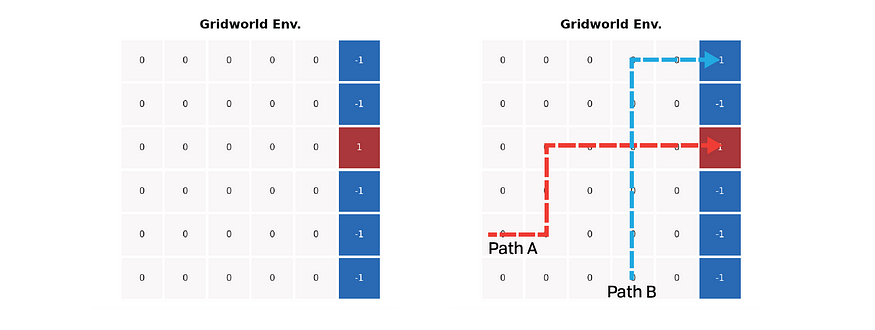
A imagem acima mostra uma configuração simples do ambiente mundial em grade. Todas as células coloridas representam estados terminais; o agente recebe uma recompensa de +1 ao entrar em uma célula vermelha, mas uma recompensa de -1 ao entrar em uma célula azul. Todas as outras etapas da grade retornam uma recompensa zero. Os dois caminhos predefinidos estão marcados no lado direito da figura acima: um atinge a célula azul e o outro para na célula vermelha; a intersecção dos caminhos ajuda a maximizar a diferença de valor entre os dois métodos.
Podemos então usar as equações da seção anterior para avaliar o ambiente. Não descontamos retornos ou estimativas e definimos α com um valor pequeno de 1e-3. Consideramos que o valor convergiu quando a soma absoluta dos incrementos de valor está abaixo do limite 1e-3.
# Monte Carlo Evaluation
def mc_sweep():
env = get_env()
V = np.zeros_like(env)
alpha = 1e-3
trajs = get_paths()
while True:
increment = np.zeros_like(V)
for traj in trajs:
G = env[traj[-1][0], traj[-1][1]]
for i in range(len(traj) - 2, -1, -1):
row, col = traj[i]
increment[row, col] += G - V[row, col]
increment *= alpha
if np.abs(increment).sum() < 1e-3:
break
V += increment
return V
# TD evaluation
def td_sweep():
env = get_env()
V = np.zeros_like(env)
alpha = 1e-3
trajs = get_paths()
while True:
increment = np.zeros_like(V)
for traj in trajs:
for i in range(len(traj) - 1):
curr_row, curr_col = traj[i]
next_row, next_col = traj[i + 1]
increment[curr_row, curr_col] += (
env[next_row, next_col]
+ V[next_row, next_col]
- V[curr_row, curr_col]
)
increment *= alpha
if np.abs(increment).sum() < 1e-3:
break
V += increment
return V
if __name__ == "__main__":
env = get_env()
V_mc = mc_sweep()
V_td = td_sweep()
V_mc[:, -1] = env[:, -1]
V_td[:, -1] = env[:, -1]
titles = ["Gridworld Env.", "Monte Carlo", "Temporal-Difference"]
plt.figure(figsize=(9, 3), dpi=300)
for i, V in enumerate([env, V_mc, V_td]):
ax = plt.subplot(1, 3, i + 1)
ax.set_title(titles[i], fontdict={"fontsize": 7, "fontweight": "bold"})
ax = sns.heatmap(
V,
linewidths=1,
annot=True,
annot_kws={"fontsize": 5},
cmap="vlag",
square=True,
cbar=False,
xticklabels=False,
yticklabels=False,
)
plt.show()Os resultados da avaliação são os seguintes:

As diferentes maneiras pelas quais os dois algoritmos estimam os valores ficam bem aparentes na figura acima. O método MC é fiel ao retorno de caminhos, portanto o valor de cada caminho indica diretamente como ele termina. Ainda assim, o método TD fornece melhores previsões, especialmente no caminho azul – os valores no caminho azul antes da intersecção também indicam a probabilidade de atingir o glóbulo vermelho.
Com este caso mínimo em mente, estamos prontos para passar para um exemplo mais complexo e tentar encontrar a diferença de desempenho entre as duas abordagens.
4. Tarefa de caminhada aleatória
A tarefa de passeio aleatório é um processo simples de recompensa de Markov proposto por Sutton et al ., para fins de previsão de TD e MC [2], conforme mostrado na figura abaixo. Nesta tarefa, o agente parte do nó central C. O agente dá um passo para a direita ou para a esquerda com igual probabilidade em cada nó. Existem dois estados terminais em ambas as extremidades da cadeia. A recompensa por ir para a extremidade esquerda é 0 e a recompensa por ir para a extremidade direita é +1. Todas as etapas antes do término rendem uma recompensa de 0.

Podemos usar o seguinte código para criar um ambiente de passeio aleatório:
import numpy as np
# Using node to represent the states and the connection between each pair
class Node:
def __init__(self, val: str):
self.value = val
self.right = None
self.left = None
self.r_reward = 0 # the reward of stepping right
self.l_reward = 0 # the reward of stepping right
def __eq__(self, other_val) -> bool:
return self.value == other_val
def __repr__(self) -> str:
return f"Node {self.value}"
# Build the Random Walk environment
class RandomWalk:
def __init__(self):
self.state_space = ["A", "B", "C", "D", "E"]
# We need to make the mapping start from 1 and reserve 0 for the terminal state
self.state_idx_map = {
letter: idx + 1 for idx, letter in enumerate(self.state_space)
}
self.initial_state = "C"
self.initial_idx = self.state_idx_map[self.initial_state]
# Build environment as a linked list
self.nodes = self.build_env()
self.reset()
def step(self, action: int) -> tuple:
assert action in [0, 1], "Action should be 0 or 1"
if action == 0:
reward = self.state.l_reward
next_state = self.state_idx_map[self.state.value] - 1
self.state = self.state.left
else:
reward = self.state.r_reward
next_state = self.state_idx_map[self.state.value] + 1
self.state = self.state.right
terminated = False if self.state else True
return next_state, reward, terminated
# reset the state to the initial node
def reset(self):
self.state = self.nodes
while self.state != self.initial_state:
self.state = self.state.right
# building the random walk environment as a linked list
def build_env(self) -> Node:
values = self.state_space
head = Node(values[0])
builder = head
prev = None
for i, val in enumerate(values):
next_node = None if i == len(values) - 1 else Node(values[i + 1])
if not next_node:
builder.r_reward = 1
builder.left = prev
builder.right = next_node
prev = builder
builder = next_node
return head=====Test: checking environment setup=====
Links: None ← Node A → Node B
Reward: 0 ← Node A → 0
Links: Node A ← Node B → Node C
Reward: 0 ← Node B → 0
Links: Node B ← Node C → Node D
Reward: 0 ← Node C → 0
Links: Node C ← Node D → Node E
Reward: 0 ← Node D → 0
Links: Node D ← Node E → None
Reward: 0 ← Node E → 1 O valor real de cada nó no ambiente sob a estratégia aleatória é [1/6, 2/6, 3/6, 4/6, 5/6]. Este valor é calculado pela avaliação da estratégia utilizando a equação de Bellam:

Nossa tarefa aqui é descobrir quão próximos os valores estimados pelos dois algoritmos estão do valor verdadeiro; podemos assumir arbitrariamente que o algoritmo produz uma função de valor que está mais próxima da função de valor verdadeiro, medida pela raiz média erro quadrático médio (RMS), indicando que o desempenho é melhor.
5. Desempenho de TD(0) e MC constante em passeio aleatório
5.1 Algoritmo
Depois que o ambiente estiver preparado, podemos começar a executar os dois métodos em um ambiente de passeio aleatório e comparar seu desempenho. Primeiro, vamos dar uma olhada nos dois algoritmos:


Conforme mencionado anteriormente, o método MC deve esperar até o final do episódio para atualizar o valor no final da trajetória, enquanto o método TD atualiza o valor de forma incremental. Essa diferença traz um truque ao inicializar a função valor-estado: em MC, a função valor-estado não inclui o estado terminal, enquanto em TD(0), a função deve incluir um estado terminal com valor 0, porque TD( 0) O método está sempre um passo à frente do final do episódio.
5.2 Implementação
A seleção do parâmetro α nesta implementação refere-se aos parâmetros propostos no livro [2], os parâmetros são [0,01, 0,02, 0,03, 0,04] para o método MC e [0,05, 0,10, 0,15] para o método TD. Eu me perguntei por que os autores não escolheram o mesmo conjunto de parâmetros em ambos os algoritmos, até executar o método MD com o parâmetro TD: o parâmetro TD é muito alto para o método MC, não revelando assim o melhor desempenho do MC. Portanto, nos ateremos às configurações deste livro nas varreduras de parâmetros. Agora, vamos executar os dois algoritmos para descobrir como eles funcionam na configuração do passeio aleatório.
5.3 Resultados
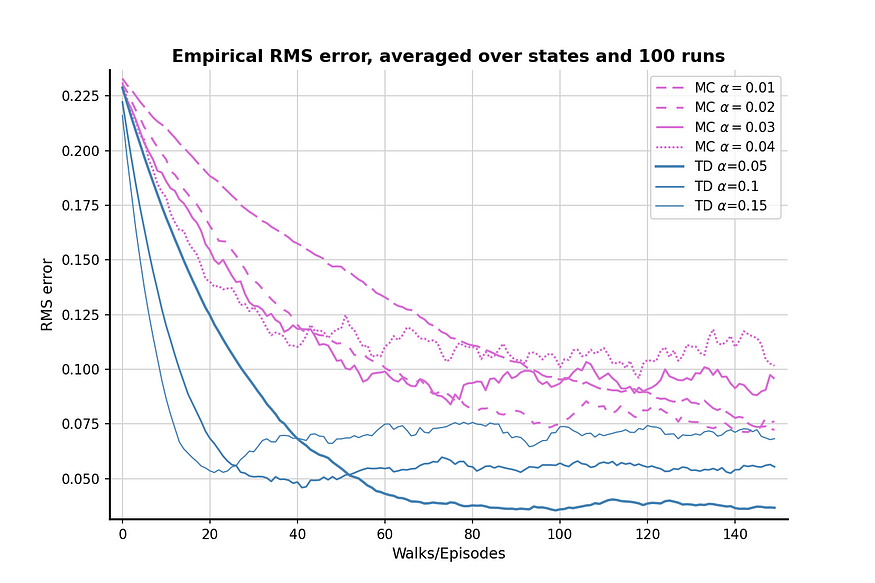
O resultado após 100 comparações é mostrado na figura acima. Os métodos TD geralmente produzem melhores estimativas de valor do que os métodos MC, e TD com α = 0,05 pode estar muito próximo do valor verdadeiro. O gráfico também mostra que o método MC tem maior variância em comparação ao método TD porque a linha orquídea flutua mais do que a linha azul aço.
É importante notar que para ambos os algoritmos, quando α é (relativamente) alto, a perda RMS primeiro diminui e depois aumenta novamente. Esse comportamento se deve ao efeito combinado da inicialização do valor e dos valores alfa. Inicializamos um valor relativamente alto de 0,5, que é superior ao valor real dos nós A e B. Como a política aleatória tem 50% de chance de escolher o passo “errado”, afastando assim o agente do estado terminal correto, um valor alto de α também enfatizará o passo errado e afastará o resultado do valor verdadeiro.
Agora vamos tentar reduzir o valor inicial para 0,1 e executar a comparação novamente para ver se o problema diminui:

Um valor inicial mais baixo obviamente ajuda a aliviar o problema; não há efeito aparente de "para baixo, depois para cima". No entanto, um efeito colateral de valores iniciais mais baixos é o aprendizado menos eficiente, uma vez que a perda RMS nunca cai abaixo de 05,150 após 0 episódios. Portanto, existe um compromisso entre valores iniciais, parâmetros e desempenho do algoritmo.
6. Treinamento em lote
O último ponto que quero destacar neste post é a comparação do treinamento em lote dos dois algoritmos.
Considere que estamos diante de uma situação em que acumulamos apenas uma quantidade finita de experiência em uma tarefa de passeio aleatório ou só podemos executar um certo número de episódios devido a restrições de tempo e computacionais. A ideia de atualização em lote [2] foi proposta para lidar com esta situação, utilizando totalmente as trajetórias existentes.
A ideia do treinamento em lote é atualizar repetidamente os valores em um lote de trajetórias até que os valores convirjam para a resposta. Esses valores só são atualizados depois que todas as experiências em lote forem totalmente processadas. Vamos implementar o treinamento em lote de ambos os algoritmos em uma configuração de passeio aleatório e ver se o método TD ainda tem um desempenho melhor que o método MC.
6.1 Resultados

Os resultados do treinamento em lote mostram que o método TD ainda tem um desempenho melhor do que o método MC com experiência limitada, e a diferença de desempenho entre os dois algoritmos é bastante óbvia.
7. Conclusão
Neste post, discutimos a diferença entre métodos α MC constantes e métodos TD(0) e comparamos seu desempenho em tarefas de passeio aleatório. Os métodos TD cobrem os métodos MC em todos os testes deste artigo, portanto é preferível tratar o TD como um método para tarefas de aprendizagem por reforço. No entanto, isso não significa que o TD seja sempre melhor que o MC, porque este último tem uma das vantagens mais óbvias: a ausência de viés. Se a tarefa que enfrentamos não tolera preconceitos, então MC pode ser uma escolha melhor; caso contrário, TD pode lidar melhor com o caso geral.
referência
[1] Termos de serviço do meio da jornada: Termos de serviço do meio da jornada
[2] Sutton, Richard S. e Andrew G. Barto. Aprendizagem por Reforço: Uma Introdução . Imprensa do MIT, 2018.
Meu repositório GitHub para este artigo: [ link ].