Zusätzliches Kapitel über die Entwicklung von Programmierern – wie man Newtons iterative Methode versteht und wie man Newtons iterative Methode verwendet, um die Quadratwurzel einer Zahl zu finden

Es ist lange her, Freunde, ich bin wieder hier, dieses Mal teile ich mit, wie man Newtons iterative Methode versteht und wie man Newtons iterative Methode verwendet, um die Quadratwurzel einer Zahl zu finden

Was ist Newtons Iterationsmethode?

Amtssprache : Die Newton-Iterationsmethode, auch bekannt als Newton-Raphson-Methode (Newton-Raphson-Methode), ist eine von Newton im 17. Jahrhundert vorgeschlagene Methode zur Approximation der Lösung von Gleichungen im reellen und komplexen Bereich.
Kurz gesagt, ein Algorithmus zur Simulation von Näherungen.

Hintergrund generiert durch Newtons iterative Methode

Für die meisten Gleichungen gibt es keine Formeln zur Wurzelfindung, daher ist es sehr schwierig oder sogar unlösbar, exakte Wurzeln zu finden. Daher ist es besonders wichtig, ungefähre Wurzeln von Gleichungen zu finden.

Wozu dient Newtons Iterationsmethode?

Newtons iterative Methode kann zur Lösung von Szenarien verwendet werden, in denen Funktionen wie arithmetische Quadratwurzeln zweite Ableitungen haben.

Die Grundidee der Newtonschen Iterationsmethode? (Nehmen Sie als Beispiel die arithmetische Quadratwurzel)

Übersicht: Durch kontinuierliches Erstellen von Tangenten, um den Schnittpunkt mit der x-Achse zu finden und sich dem Nullpunkt unendlich zu nähern

1. Der Konstruktor y=x^2 - n
   
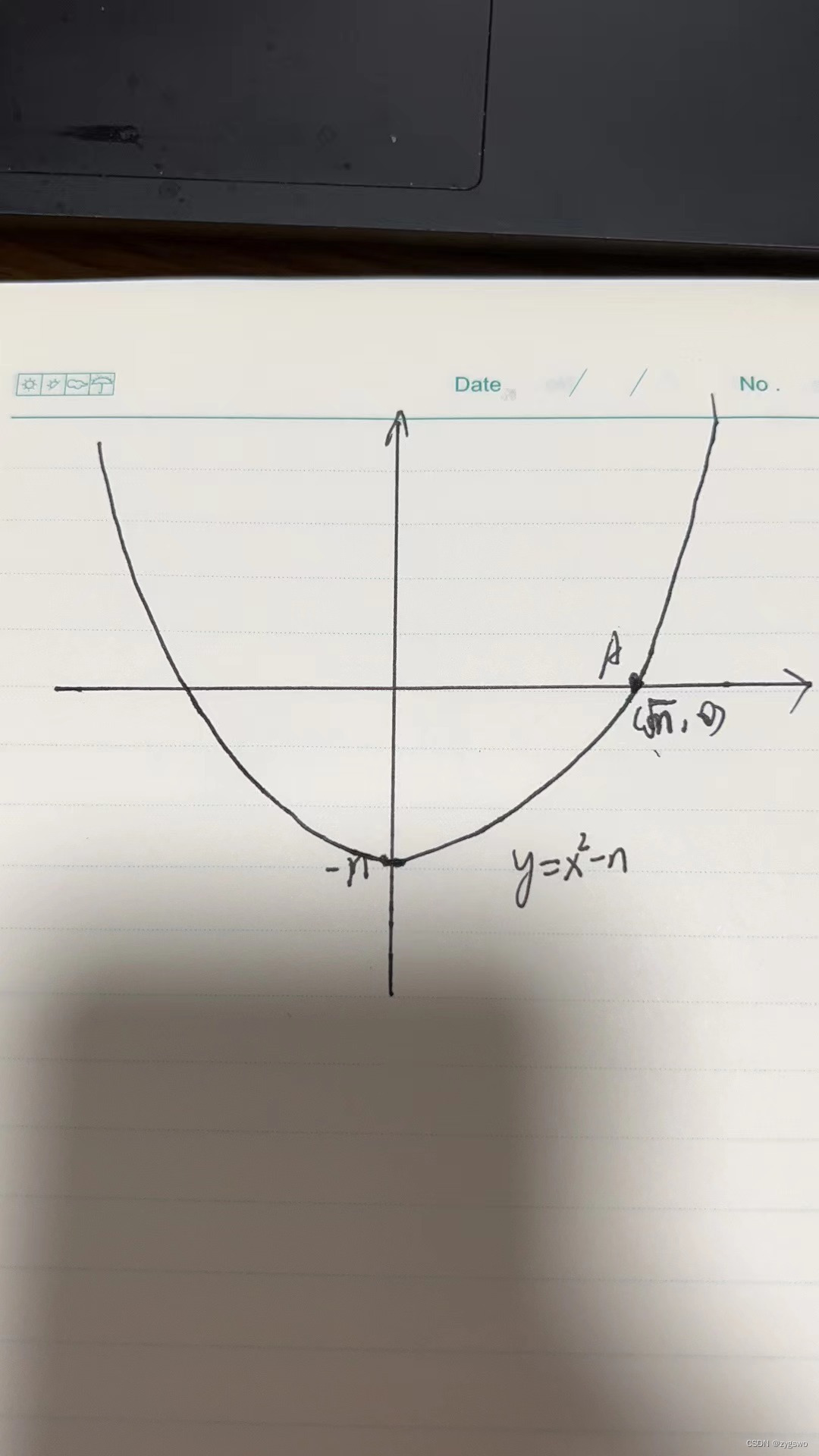
   erklärt hier den Grund für diese Konstruktion. Wenn y=0 ist, ist der Wert von x die erforderliche Quadratzahl, und diese Funktion kann zweimal abgeleitet werden, sodass die Wurzel mit der Newton-Iterationsmethode gefunden werden kann Ungefährer Wert von n
2. Nehmen Sie danach den Punkt C(1, 1-n) nahe 0 und ziehen Sie dann die Tangente der Funktion durch diesen Punkt, um die x-Achse am Punkt B(k', 0) zu schneiden, und finden Sie den Punkt B '(k) auf der Funktion, wenn x=k'',k'^2 - n)
   
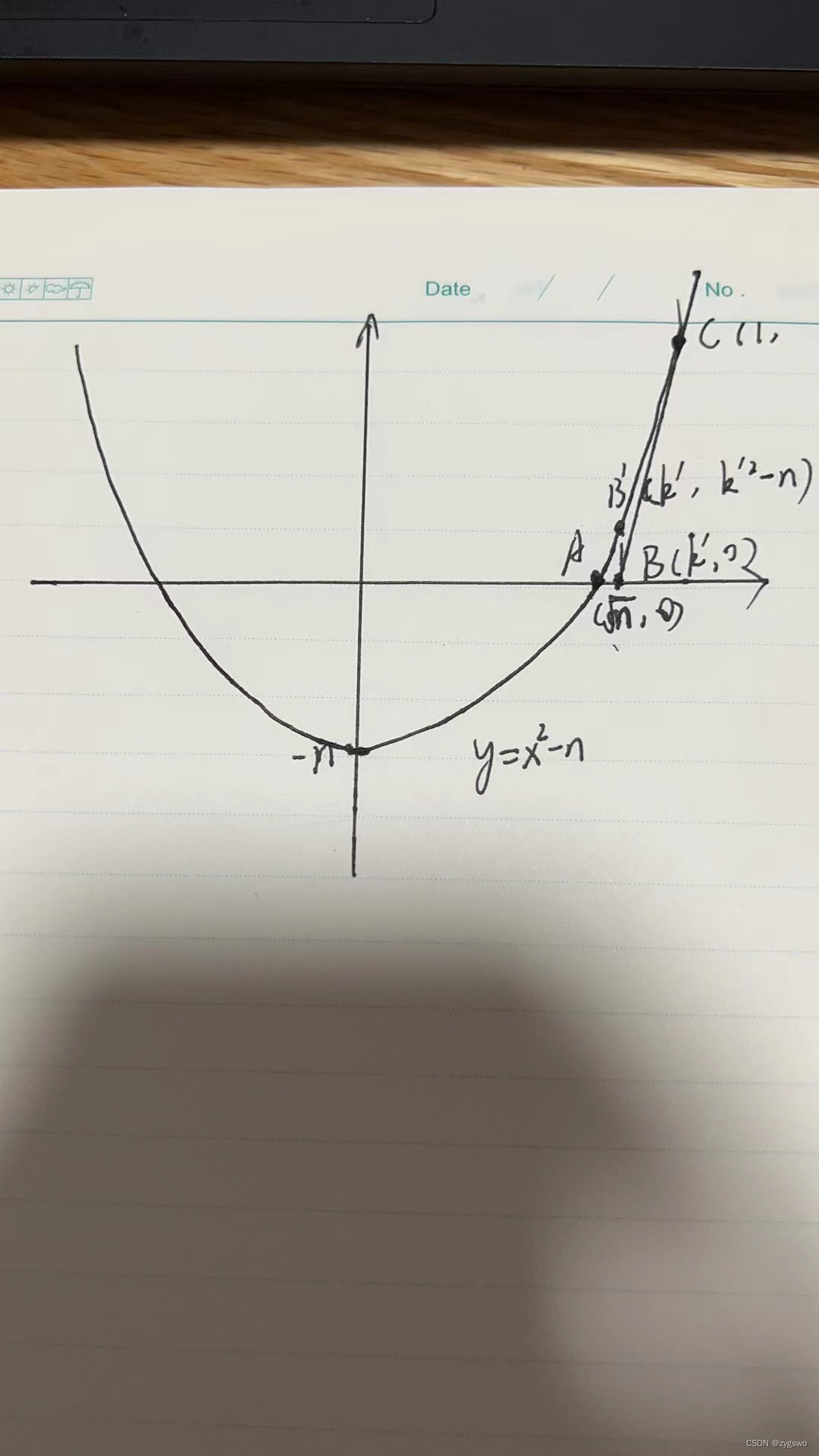
3. Nach unendlichen Iterationen, nach vielen Iterationen haben wir festgestellt, dass dieser Wert immer näher an A(Quadratwurzel n,0) herankommt.
4. Der Wert des Grenzwerts ist der Wert der Quadratwurzel n

Der Code zum Finden der Quadratwurzel der iterativen Methode von Newton

public static double sqrt(double n) {
    
    
    double threshold= 1e-15;
    double k = 1.0;
    while (Math.abs(k*k - n) > threshold) {
    
    
        k = (k + n/k) / 2.0;
    }
    return k;
}

Beweis für die Bestimmung der Quadratwurzel der iterativen Methode von Newton

1. Die bekannte konstruierte Funktion ist y = x^2 - n
2. Sei C ein Punkt auf der Funktion und der Abszissenwert von C wird auf k gesetzt, d. h. x = k, und y = k^2 - n, d. h. C(k,k^2-n).
3. Die Steigung der Tangente am Punkt C wird auf m = (x^2 - n)' = 2x = 2k gesetzt
4. Dann gibt es den Schnittpunkt B(k',0) der Tangente und der Abszisse und m = Δy/Δx, dann gibt es Δx = Δy/m = (k^2 - n)/ 2k, also gibt es k' = k - Δx = k - (k^2 - n)/ 2k = (k^2 + n)/2k = (k + n/k) / 2, dann verwenden Sie den Punkt von x=k' auf dem Funktionieren Sie als Punkt C, um Schritt 2, 3, 4 zu wiederholen
5. Wenn Δy -> 0, d. h. k^2 - n -> 0, d. h. wenn Punkt C sich unendlich Null nähert, ist k die gesuchte Lösung, d. h. die Wurzelzahl n
6. Vollendet

————————————— Wenn Sie Fragen haben, hinterlassen Sie bitte eine Nachricht im Kommentarbereich ——————————