[Estrutura de dados e implementação do algoritmo C++] 2. Pesquisa binária e recursão simples

O vídeo original é o ensino da estação B de Zuo Chengyun

---

---

1 dicotomia

Pesquisa binária é um algoritmo de pesquisa para encontrar um elemento específico em uma matriz ordenada . Sua ideia básica é dividir a matriz do meio e, em seguida, julgar a relação de tamanho entre o elemento de destino e o elemento do meio para determinar se o elemento de destino está na metade esquerda ou na metade direita. Em seguida, continue a executar a mesma operação no subarray correspondente até que o elemento de destino seja encontrado ou seja determinado que o elemento de destino não existe.

As etapas específicas são as seguintes:

• Define o limite esquerdo da matriz para a esquerda e o limite direito para a direita.
• Calcule a posição intermediária do meio, ou seja, meio = (esquerda + direita) / 2.
• Compare a relação de tamanho entre o elemento de destino e o elemento intermediário:
• Se o elemento de destino for igual ao elemento do meio, o elemento de destino será encontrado e seu índice será retornado.
• Se o elemento de destino for menor que o elemento do meio, atualize o limite direito right = mid - 1 e continue a pesquisa binária na metade esquerda.
• Se o elemento de destino for maior que o elemento do meio, atualize o limite esquerdo left = mid + 1 e continue a pesquisa binária na metade direita.
• Repita as etapas 2 e 3 até que o elemento de destino seja encontrado ou o limite esquerdo seja maior que o limite direito.

Complexidade de tempo O(logN) , onde n é o comprimento da matriz. Como o intervalo de pesquisa é reduzido pela metade a cada vez, o algoritmo é muito eficiente. Mas a matriz precisa ser ordenada, caso contrário, a dicotomia não pode ser aplicada para pesquisa.

1.1 有序Encontre um elemento específico em uma matriz

A ideia básica é reduzir o intervalo de pesquisa pela metade comparando a relação de tamanho entre o elemento intermediário e o elemento de destino até que o elemento de destino seja encontrado ou o intervalo de pesquisa esteja vazio.

Como, por exemplo, o número de arrays é N=16, o pior caso é dividido em 4 vezes $([8|8]\to [4|4]\to [2|2]\to [1|1])$ , e$4=lo{g}_{}16$ . Ou seja, a complexidade de tempo é$O\left(logN\right)$

/* 注意：题目保证数组不为空，且 n 大于等于 1 ，以下问题默认相同 */
int binarySearch(std::vector<int>& arr, int value)
{
    
    
    int left = 0;
    int right = arr.size() - 1;
    // 如果这里是 int right = arr.size() 的话，那么下面有两处地方需要修改，以保证一一对应：
    // 1、下面循环的条件则是 while(left < right)
    // 2、循环内当 array[middle] > value 的时候，right = middle

    while (left <= right)
    {
    
    
        int middle = left + ((right - left) >> 1);  // 不用right+left，避免int溢出，且更快
        if (array[middle] > value)
            right = middle - 1;
        else if (array[middle] < value)
            left = middle + 1;
        else
            return middle;
        // 可能会有读者认为刚开始时就要判断相等，但毕竟数组中不相等的情况更多
        // 如果每次循环都判断一下是否相等，将耗费时间
    }
    return -1;
}

Cuidado com esquerda + ((direita - esquerda) >> 1) resultados etc para (direita + esquerda) / 2, mas mais rápido sem estouro int

1.2 Encontre a posição mais à esquerda de >= um certo número em uma matriz ordenada

A ideia ainda é o método da dicotomia, que é diferente de encontrar um determinado valor e parar a dicotomia quando o valor alvo for encontrado. O problema de encontrar a posição mais à esquerda/mais à direita deve ser dicotômico até o fim

int nearLeftSearch(const std::vector<int>& arr, int target)
{
    
    
	int left = 0;
	int right = arr.size() - 1;
	int result = -1;
	
	while (left <= right)
	{
    
    
		int mid = left + ((right - left) >> 1);
		if (target <= arr[mid]){
    
     // 目标值小于等于mid，就要往左继续找
			result = mid;// 暂时记录下这个位置，因为左边可能全都比目标值小了，就已经找到了
			right = mid - 1;
		} else{
    
    		// target > arr[mid]
			left = mid + 1;
		}
	}
	return result;
}

1.3 Encontre a posição mais à direita de <= um certo número em uma matriz ordenada

• Se o elemento do meio for maior que o valor de destino, isso significa que o valor de destino deve estar na metade esquerda, portanto, limitamos a pesquisa à metade esquerda e atualizamos da direita para o meio - 1.
• Se o elemento do meio for menor ou igual ao valor de destino, isso significa que o valor de destino deve estar na metade direita ou na posição atual, portanto, atualizamos o resultado para o índice do meio atual mid para registrar a posição mais à direita encontrada e restringir o intervalo de pesquisa para a metade direita, atualização da esquerda para o meio + 1.

int nearRightSearch(const std::vector<int>& arr, int target) 
{
    
    
    int left = 0;
    int right = arr.size() - 1;
    int result = -1;

    while (left <= right) {
    
    
        int mid = left + (right - left) / 2;

        if (target < arr[mid]) {
    
    
            right = mid - 1;
        } else {
    
    	// target >= arr[mid]
            result = mid;
            left = mid + 1;
        }
    }

    return result;
}

1.4 Problema de mínimo local (um caso de arranjo não ordenado usando dicotomia)

A matriz arr não está ordenada, quaisquer dois números adjacentes não são iguais , encontre uma posição mínima local (valor mínimo) e a complexidade de tempo deve ser melhor que O(N)

A desordem também pode ser dicotomizada , desde que o problema-alvo deva ter uma solução de um lado e o outro lado não importe, a dicotomia pode ser usada

1. Primeiro, julgue os dois limites da matriz

• Encontrado se o limite esquerdo arr[0] < arr[1]
• Encontrado se houver um limite arr[n-1] < arr[n-2]
• Se nenhum dos dois limites for um mínimo local, e porque quaisquer dois números adjacentes não são iguais, o limite esquerdo é monotonicamente decrescente localmente e o limite direito é monotonicamente crescente localmente . Portanto, na matriz, deve haver um ponto de valor mínimo
  

2. Faça a dicotomia e julgue a relação entre as posições intermediária e adjacente, que se dividem em 3 situações: (Lembrete: dois elementos adjacentes na matriz não são iguais!) 3. Repita o processo 2

até encontrar o valor mínimo

int LocalMinimumSearch(const std::vector<int>& arr) 
{
    
    
    int n = arr.size();
    // 先判断元素个数为0，1的情况，如果题目给出最少元素个>1数则不需要判断
    if (n == 0) return -1;
    if (n == 1) return 0; // 只有一个元素，则是局部最小值
	
	if (arr[0] < arr[1]) return 0;
	
	int left = 0;
    int right = n - 1;
	// 再次提醒，数组中相邻两个元素是不相等的！
    while (left < right) 
    {
    
    
        int mid = left + ((right - left) >> 1);

        if (arr[mid] < arr[mid - 1] && arr[mid] < arr[mid + 1]) {
    
    
            return mid;  // 找到局部最小值的位置
        } else if (arr[mid - 1] < arr[mid]) {
    
    
            right = mid - 1;  // 局部最小值可能在左侧
        } else {
    
    
            left = mid + 1;  // 局部最小值可能在右侧
        }
    }

    // 数组中只有一个元素，将其视为局部最小值
    return left;
}

2 Pensamento recursivo simples

Desde o início do Zuoge P4 , pertence ao pré-conhecimento do merge sort. A dicotomia também é usada aqui. Principalmente para entender o processo de execução

Exemplo: encontre o valor máximo no intervalo especificado da matriz, usando recursão para obter

#incldue <vector>
#include <algorithm>
int process(const std::vector<int>& arr, int L, int R)
{
    
    
	if (L == R) return arr[L]; 
	
	int mid = L + ((R - L) >> 1);	// 求中点,右移1位相当于除以2
	int leftMax = process(arr, L, mid);
	int rightMax = process(arr, mid + 1, R);
	return std::max(leftMax, rightMax);
}

Quando a função process(arr, L, R) é chamada, ela faz o seguinte:

1. Primeiro, a condição de término da recursão é verificada. Se L e R forem iguais, significa que o intervalo mínimo da matriz foi recursado e há apenas um elemento. Neste momento, o elemento arr[L] é retornado diretamente.
2. Se a condição de término não for atendida, a recursão precisa continuar. Primeiro, calcule o ponto médio e divida o intervalo [L, R] em dois subintervalos [L, mid] e [mid+1, R].
3. Em seguida, chame recursivamente process(arr, L, mid) para processar o subintervalo esquerdo. Essa etapa coloca a função atual na pilha, inserindo um novo nível de recursão.
4. No novo nível recursivo, execute as etapas 1 a 3 novamente até que a condição de término seja satisfeita e retorne o valor máximo leftMax do subintervalo esquerdo.
5. Em seguida, chame recursivamente process(arr, mid+1, R) para processar o subintervalo correto. Novamente, esta etapa coloca a função atual na pilha, inserindo um novo nível de recursão.
6. No novo nível recursivo, execute as etapas 1 a 3 novamente até que a condição de término seja satisfeita e retorne o valor máximo rightMax do subintervalo direito.
7. Por fim, compare os valores máximos leftMax e rightMax dos subintervalos esquerdo e direito, tome o maior valor como o
   valor máximo de todo o intervalo [L, R] e retorne-o como resultado.
8. Ao retornar recursivamente para a camada anterior, passe o valor máximo obtido para a camada anterior até retornar ao ponto de chamada original para obter o valor máximo de todo o array.

No processo de recursão, cada chamada recursiva criará um novo quadro de pilha de funções para salvar as variáveis ​​locais e os parâmetros da função. Quando a condição de término é atendida, a recursão começa a retroceder e o resultado final é retornado camada por camada. Ao mesmo tempo, as variáveis ​​locais e os parâmetros de cada camada também são destruídos e os quadros da pilha de funções são retirados da pilha por sua vez.

gráfico de dependência

• Suponha que a matriz de destino seja [3, 2, 5, 6, 7, 4], chame process(0,5) para encontrar o valor máximo e o parâmetro arr seja omitido
• O número vermelho é o fluxo de execução do processo, que omite o processo de comparação e retorno de std::max
  

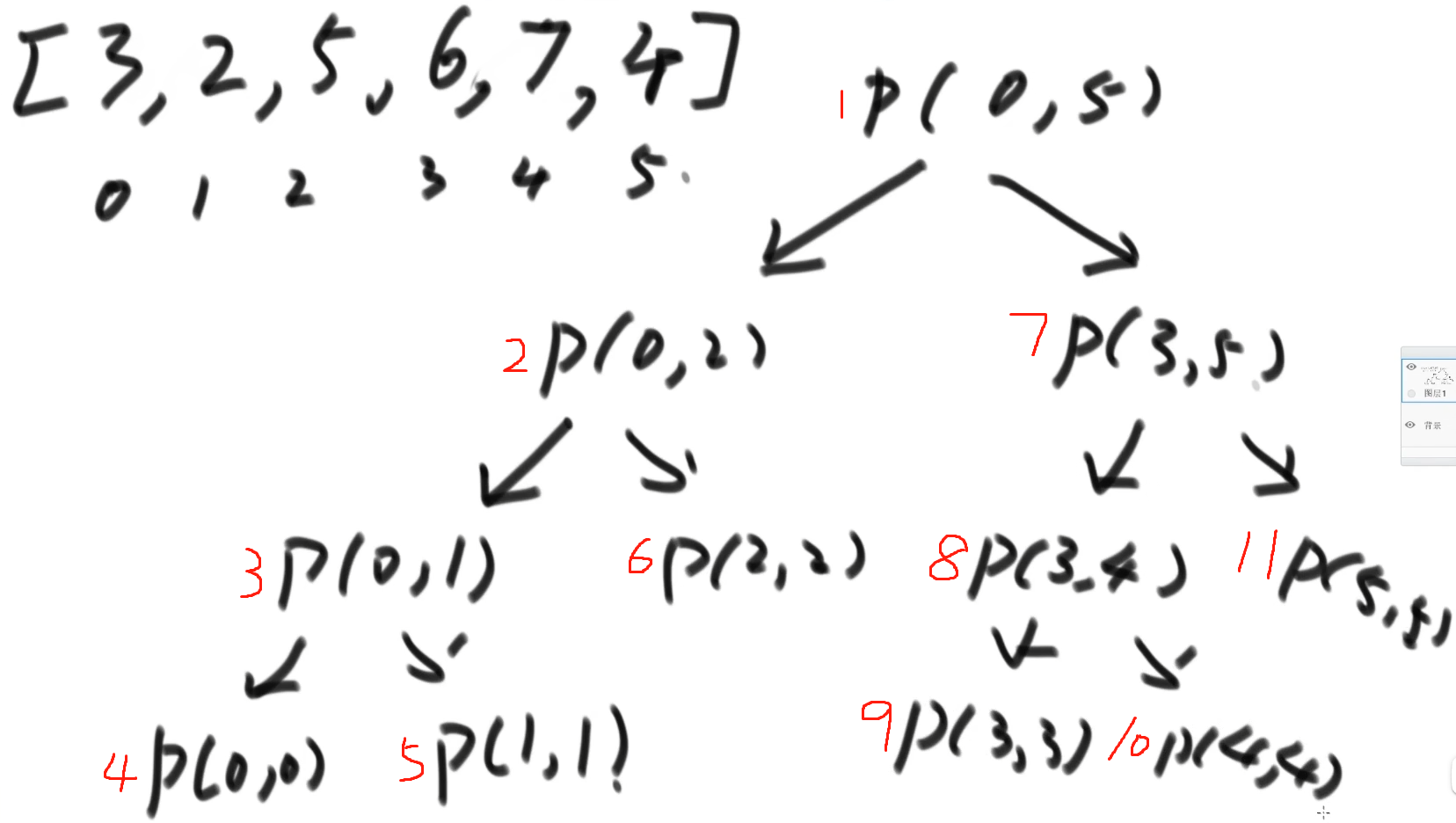
Palavras humanas: Se você deseja obter o valor de retorno do array, ou seja, 1o valor de retorno da primeira etapa, primeiro deve obter 2o valor máximo, e seu valor máximo deve ser executado primeiro de acordo com o código 3e 3deve também será executado primeiro 4. Quando os dois pontos atingirem 4esta etapa, há apenas um elemento L==R, observe o código, este elemento é o valor máximo do intervalo atual (0,0), retorne para, 3após 3obter leftMax , você precisa do valor máximo da parte direita, execute-o 5, obtenha rightMax e, finalmente, compare o valor máximo dos intervalos esquerdo e direito, obtenha o valor máximo do intervalo (0,1) e retorne a ele 2. 2é necessário 6retornar para obter o valor máximo de (0,2) após a comparação 6e 2retornar a ele 1. Então faça o da direita. . . . mais tarde omitido

2.1 Complexidade de Tempo do Algoritmo Recursivo (Fórmula Mestre)

Na programação, a recursão é um algoritmo muito comum. É amplamente utilizado devido ao seu código conciso. No entanto, em comparação com a execução sequencial ou programas cíclicos, a recursão é difícil de calcular. A fórmula mestre é usada para calcular a complexidade de tempo dos programas recursivos.

Condições de uso: Todos os subproblemas devem ter o mesmo tamanho . Para ser franco, é basicamente o algoritmo recursivo criado por árvores binárias e binárias.

公式: $T\left(N\right)=aT(N/b)+O\left(N^d\right)$

• $N$ : o tamanho dos dados do processo pai é N
• $N/b$ : Tamanho dos dados do subprocesso
• $a$ : o número de chamadas para a sub-rotina
• $O\left(N^d\right)$: Complexidade de tempo de outros processos, exceto a invocação de subproblemas

Depois de obter o abd, obtenha a complexidade de tempo de acordo com as seguintes situações diferentes

• $lo{g}_{}a>d$ : complexidade de tempo é$O\left(N^{lo{g}_{}a}\right)$
• $lo{g}_{}a=d$ : A complexidade de tempo é$O(N^d\cdot logN)\_\_$
• $lo{g}_{}a<d$ : A complexidade de tempo é$O\left(N^d\right)$

Por exemplo, o exemplo de encontrar o valor máximo mencionado acima pode usar esta fórmula:

$N=2\cdot T\left(\frac{}{2}\right)+O\left(1\right)$ . onde a = 2; b = 2; d = 0

$lo{g}_{}2=1>0$ Portanto, a complexidade de tempo é:$O\left(N\right)$