Chapitre 2 Complexité temporelle et spatiale des algorithmes
1. Efficacité algorithmique
Comment mesurer la qualité d'un algorithme ?
Généralement , elle est mesurée par la complexité temporelle et la complexité spatiale de l'algorithme.
La complexité temporelle mesure principalement la vitesse d'exécution d'un algorithme , tandis que la complexité spatiale mesure principalement l'espace supplémentaire requis pour exécuter un algorithme . Au début du développement informatique, la capacité de stockage des ordinateurs était très faible. Il est donc très préoccupé par la complexité de l'espace. Mais après le développement rapide de l'industrie informatique,
la capacité de stockage de l'ordinateur a atteint un niveau très élevé. Nous n'avons donc plus besoin de prêter une attention particulière à la complexité spatiale d'un algorithme .
2 fois la complexité
2.1 Le concept de complexité temporelle
Définition : En informatique, la complexité temporelle d'un algorithme est une fonction qui décrit quantitativement le temps d'exécution de cet algorithme. Le nombre d'exécutions des opérations de base dans l'algorithme est la complexité temporelle de l'algorithme.
C'est-à-dire : trouver l'expression mathématique entre un certain énoncé de base et la taille du problème N, c'est calculer la complexité temporelle de l'algorithme.
Exemple:
Q : Combien de fois l'instruction ++count dans Func1 est-elle exécutée ?
void Func1(int N)
{
int count = 0;
for (int i = 0; i < N; ++i)
{
for (int j = 0; j < N; ++j)
{
++count;
}
}
for (int k = 0; k < 2 * N; ++k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}
}
Le nombre d'exécutions est exprimé comme une fonction comme suit :
F(N) = N^2^ + 2 * N + 10Du point de vue des fonctions mathématiques,
l'image de 2 * N + 10 au résultat de l'opération finale de la fonction devient progressivement plus petite à mesure que N augmente. Lorsque la zone N est infinie, nous pouvons même l'ignorer, c'est-à-dire le résultat final de la fonction tend vers N. Elle n'est liée à N 2
.
2.2 Notation asymptotique pour Big O
Notation Big O : est une notation mathématique utilisée pour décrire le comportement asymptotique d'une fonction.
Dérivez la méthode big-O :
- Remplacez toutes les constantes additives à l'exécution par la constante 1 (si le nombre d'exécutions de l'instruction de base d'une fonction est une certaine constante).
- Dans la fonction des temps d'exécution modifiés, seuls les termes d'ordre le plus élevé sont conservés.
- Si le terme d'ordre le plus élevé existe et n'est pas 1, supprimer la constante multipliée par ce terme (c'est-à-dire supprimer le coefficient du terme d'ordre le plus élevé). Le résultat est une commande big-O.(La complexité temporelle est mesurée en ordres de grandeur)
Après avoir utilisé la notation asymptotique big-O, la complexité temporelle de Func1 est :
O (N 2 )
À travers ce qui précède, nous constaterons que la représentation asymptotique du grand O supprime les éléments qui ont peu d'effet sur le résultat et montre le nombre d'exécutions de manière succincte et claire.
De plus, la complexité temporelle de certains algorithmes a un cas meilleur, moyen et pire :
Dans le pire des cas : nombre maximal d'exécutions pour toute taille d'entrée (limite supérieure)
Cas moyen : nombre d'exécutions souhaité pour toute taille d'entrée
Meilleur cas : nombre minimal d'exécutions pour toute taille d'entrée (limite inférieure)
En pratique, la préoccupation générale est le pire cas de fonctionnement de l'algorithme, de sorte que la complexité temporelle de la recherche de données dans le tableau est O (N).
2.3 Exemple de calcul de complexité temporelle
2.3.1 Exemple 1
// 计算Func2的时间复杂度?
void Func2(int N)
{
int count = 0;
for (int k = 0; k < 2 * N; ++k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}
printf("%d\n", count);
}
L'opération de base est effectuée 2N+10 fois, et la complexité temporelle est O(N) en dérivant la grande méthode d'ordre O.
2.3.2 Exemple 2
// 计算Func3的时间复杂度?
void Func3(int N, int M)
{
int count = 0;
for (int k = 0; k < M; ++k)
{
++count;
}
for (int k = 0; k < N; ++k)
{
++count;
}
printf("%d\n", count);
}
L'opération de base est effectuée M+N fois, il y a deux inconnues M et N, et la complexité temporelle est O(N+M)
Conclusion : La complexité temporelle n'a pas forcément une seule inconnue, mais il peut y en avoir deux, cela dépend des inconnues de paramètres spécifiques, mais si le titre nous dit :
- M est beaucoup plus grand que N, et la complexité temporelle devient O(M).
- M et N ont à peu près la même taille, et la complexité temporelle deviendra O(M) ou O(N), qui peuvent toutes deux être écrites.
2.3.3 Exemple 3
// 计算Func4的时间复杂度?
void Func4(int N)
{
int count = 0;
for (int k = 0; k < 100; ++k)
{
++count;
}
printf("%d\n", count);
}
L'opération de base est effectuée 100 fois et la complexité temporelle est O (1) en dérivant la méthode du grand O-ordre
2.3.4 Exemple 4
//计算strchr的时间复杂度?
const char* strchr(const char* str, int character);
Voici une implémentation approximative de cette fonction :
while(*str)
{
if(*str == character)
return str;
else
++str;
}
return NULL;
L'opération de base est mieux exécutée une fois, la pire est N fois, la complexité temporelle est généralement la pire et la complexité temporelle est O(N)
2.3.5 Exemple 5
//计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}
Remarque : La boucle à deux couches n'est pas nécessairement O(N 2 ), mais dépend également de l'implémentation spécifique de la fonction.
Nombre de premières comparaisons : N - 1
第二次比较次数:N - 2
第三次比较次数:N - 3
···
第N-1次比较次数:1
最坏情况:F(N) = (N*(N-1))/2
最好情况:F(N) = N - 1(比较第一轮,没有发生交换,说明所给数据是有序的,就不必继续进行排序)
复杂度:O(N2)(取最坏的情况)
2.3.6 实例6
//计算BinarySearch的时间复杂度?
int BinarySearch(int* a, int n, int x)
{
assert(a);
int begin = 0;
int end = n;
while (begin < end)
{
int mid = begin + ((end - begin) >> 1);
//用右移运算符是为了防止(end+begin)的值溢出,超出最大整数值
if (a[mid] < x)
begin = mid + 1;
else if (a[mid] > x)
end = mid;
else
return mid;
}
return -1;
}
上述代码采用了二分查找法。
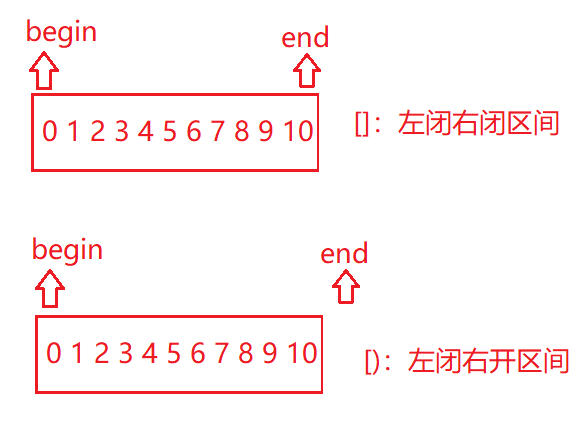
上面的代码是左闭右开区间,两种写法的区别就是对于边界的处理,无论是哪种区间,都应该贯彻保持到底,下面是左闭右闭区间的二分查找法代码:
int BinarySearch(int* a, int n, int x)
{
assert(a);
int begin = 0;
int end = n - 1;
while (begin <= end)
{
int mid = begin + ((end - begin) >> 1);
if (a[mid] < x)
begin = mid + 1;
else if (a[mid] > x)
end = mid - 1;
else
return mid;
}
return -1;
}
最好情况:O(1)
最坏情况:
假设我们找了X次,最后只剩一个元素,我们仍然没有找到,那么
1(剩下的一个元素) * 2X = N
X = log2N
时间复杂度:O(log2N)(有的简写成logN,甚至有的还会简写成lgN,但是最后这种写法是存在误差的,也是不推荐的)
结论:要准确分析算法的思想,而不要仅看循环的层数。
2.3.7 实例7
//计算阶乘递归Fac的时间复杂度?
long long Fac(size_t N)
{
if (0 == N)
return 1;
return Fac(N - 1) * N;
}
通过计算分析发现基本操作递归了N次(当然,函数调用的次数是N+1次),时间复杂度为O(N)。
下面是上面函数的变形:
long long Fac(size_t N)
{
if (0 == N)
return 1;
for(size_t i = 0;i < N;i++)
{
printf("%d",i);//看这个语句的执行次数
}
return Fac(N - 1) * N;
}
第一次函数调用:N
第二次函数调用:N - 1
···
第N次函数调用:1
第N + 1次函数调用:0(for循环无法进行,因为N = 0)
F(N) = (N + 1) * N / 2
所以时间复杂度为:O(N2)
注意:
递归算法时间复杂度计算:
- 每次函数调用是O(1),那么就看它的递归次数
- Chaque appel de fonction n'est pas O(1), cela dépend du cumul du nombre d'appels récursifs.
2.3.8 Exemple 8
//计算斐波那契递归Fib的时间复杂度?
long long Fib(size_t N)
{
if (N < 3)
return 1;
return Fib(N - 1) + Fib(N - 2);
}
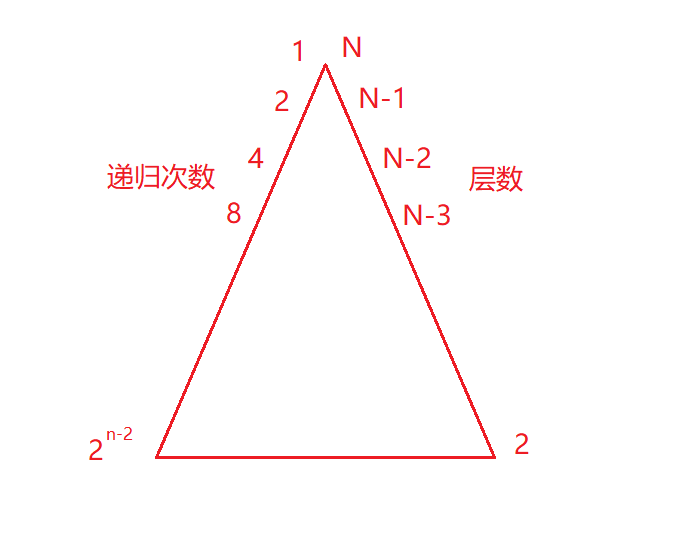
À ce stade, vous pouvez utiliser la formule de la série proportionnelle pour calculer (1*(1 - 2 N-1 ))/(1-2) = 2 N-1 -
1 (à ce moment, nous avons imaginé une situation complète, mais dans fait Y a-t-il un endroit où il est plein, par exemple, il n'y a pas de place dans le coin inférieur droit au-dessus, car ces chiffres sont relativement petits et ne peuvent pas y parvenir)Grâce à une analyse informatique, on constate que l'opération de base se répète 2 N fois (2 N-1 est considéré comme une puissance de 2 N ) fois et que la complexité temporelle est O(2 N ).
3. Complexité spatiale
La complexité de l'espace est également une expression mathématique, qui est une mesure de la quantité d'espace de stockage temporairement occupée par un algorithme pendant son fonctionnement.
La complexité de l'espace n'est pas le nombre d'octets d'espace occupé par le programme, car cela n'a pas beaucoup de sens, donc ** la complexité de l'espace compte le nombre de variables. **
Les règles de calcul de la complexité spatiale sont fondamentalement similaires à la complexité pratique et utilisent également la notation asymptotique big-O.
Remarque : L'espace de pile (paramètres de stockage, variables locales, certaines informations de registre, etc.) requis par la fonction pour s'exécuter a été déterminé lors de la compilation, de sorte que la complexité de l'espace est principalement déterminée par l'espace supplémentaire explicitement demandé par la fonction au moment de l'exécution.
3.1 Exemple 1 :
//计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}
Analyse : Un total de trois variables de fin, d'échange et de i sont ouvertes, c'est-à-dire qu'une quantité constante d'espace supplémentaire est utilisée, de sorte que la complexité de l'espace est O (1).
3.2 Exemple 2 :
//计算Fibonacci的空间复杂度?
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{
if (n == 0)
return NULL;
long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n; ++i)
{
fibArray[i] = fibArray[i - 1] + fibArray[i - 2];
}
return fibArray;
}
Analyse : Un total de (n+1) espaces entiers sont dynamiquement ouverts, donc la complexité de l'espace est O(N).
3.3 Exemple 3 :
//计算阶乘递归Fac的空间复杂度?
long long Fac(size_t N)
{
if (N == 0)
return 1;
return Fac(N - 1) * N;
}
Analyse : L'appel récursif est effectué N fois, et N cadres de pile sont ouverts, et chaque cadre de pile utilise une quantité constante d'espace. La complexité spatiale est O(N)
3.4 Exemple 4
//计算斐波那契递归Fib的空间复杂度?
long long Fib(size_t N)
{
if (N < 3)
return 1;
return Fib(N - 1) + Fib(N - 2);
}
Remarque : Le temps est cumulatif et l'espace peut être réutilisé.
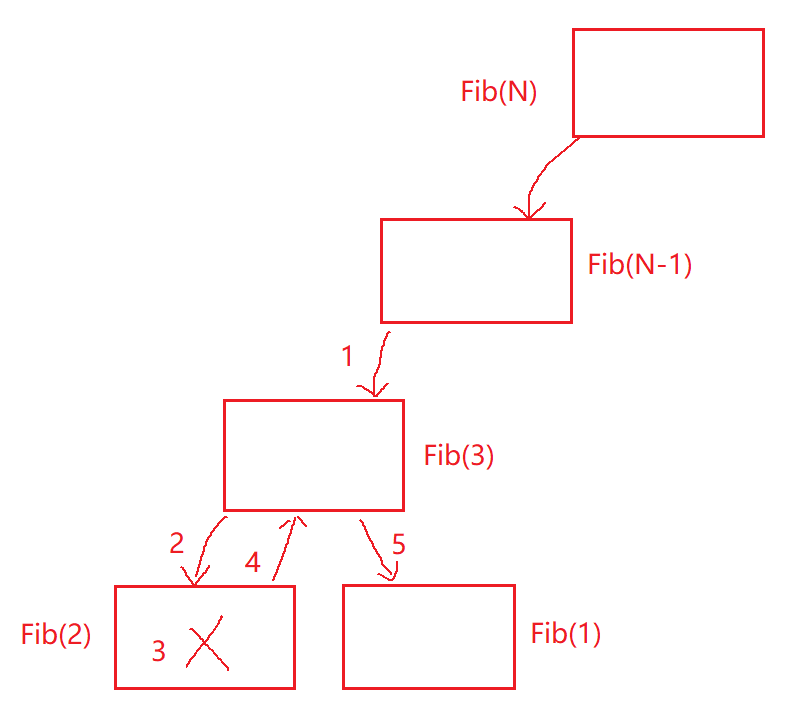
Analyse : Après avoir appelé Fib(3), appelez d'abord Fib(2). Après l'appel de Fib(2), le cadre de pile de Fib(2) sera détruit. Une fois le cadre de pile de Fib(2) détruit, continuez pour appeler Fib(1), l'espace utilisé par le cadre de pile Fib(1) à ce moment est le même espace que l'espace utilisé par le cadre de pile Fib(2) tout à l'heure. L'espace occupé par les cadres de pile ouverts par la même couche est le même espace. C'est,À un moment donné, un total de cadres de pile N-1 sont ouverts, de sorte que la complexité de l'espace est O(N).
Par exemple:
Explication : Après la destruction de l'espace du cadre de pile de f1, f2 écrase l'espace du cadre de pile f1 d'origine.(La destruction de l'espace n'est que pour rendre le droit d'utilisation au système)
4. Comparaison de complexité commune
La complexité commune de l'algorithme général est la suivante :
| 5201314 | O(1) | ordre constant |
|---|---|---|
| 3n + 4 | Au) | Ordre linéaire |
| 3n 2 + 4*n + 5 | O(n 2 ) | Commande carrée |
| 3log 2 n + 4 | O(log 2 n) | logarithmique |
| 2n + 3nlog 2 n + 4 | O(nlog 2 n) | nlog 2 nième commande |
| n 3 + 2n 2 + 4n + 6 | O(n 3 ) | ordre cubique |
| 2 n | O(2^n) | Ordre exponentiel |
Comparaison de complexité :
O(n!) > O(2 n ) > O(n 2 ) > O(nlog 2 n) > O(n) > O(log 2 n) > O(1)
5. jo exercices pour la complexité
5.1 Numéros qui disparaissent
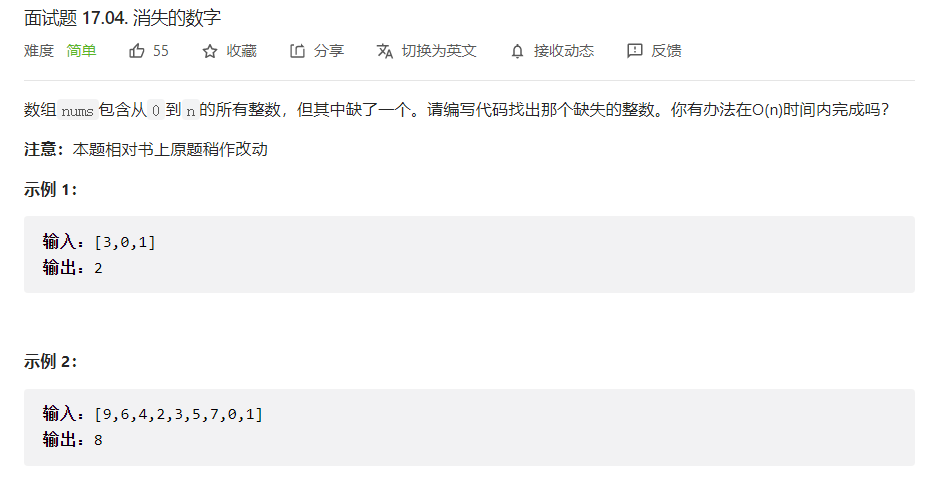
Solution:
sort (bulle(N 2 ), qsort(nlog 2 N)) (non éligible)
Mapping (méthode des indices : à combien d'indices chaque valeur correspond) (O(N)), mais cette méthode a une complexité d'espace O(N)
Affichage des codes :
int *ret = (int*)malloc(sizeof(int)*(numsSize+1)); int i = 0; for(i = 0;i<numsSize+1;i++) { ret[i] = -1; } for(i = 0;i<numsSize;i++) { ret[nums[i]] = nums[i]; } for(i = 0;i<numsSize+1;i++) { if(ret[i]==-1) { return i; } } return -1; } ```XOR (utilisez une valeur variable pour XOR les données de 0 à N, puis XOR avec les données données) (O(N))
int value = 0; int i = 0; for (i = 0; i <= numsSize; i++) { value ^= i; } for (i = 0; i < numsSize; i++) { value ^= nums[i]; } return value; } ```Formule arithmétique . Soustrayez toutes les données du tableau d'origine de la somme de 0 ~ N. (AU))
int sum = 0; int i = 0; int n = numsSize; sum = (n + 1) * n / 2;//等差数列的和的公式 for (i = 0; i < numsSize; i++) { sum -= nums[i]; } return sum; } ```
5.2 Réseaux rotatifs
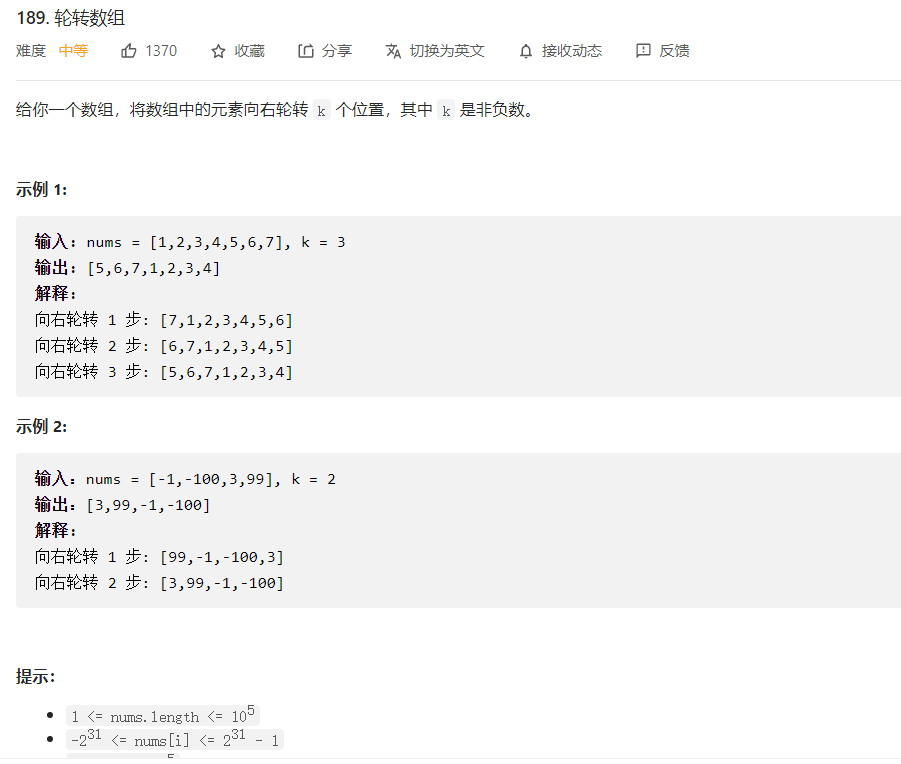
Avancée:
- Trouvez autant de solutions que possible, il y a au moins trois façons différentes d'aborder ce problème.
- Pouvez-vous résoudre ce problème en utilisant un algorithme en place
O(1)avec une complexité spatiale ?
Faites pivoter vers la droite k fois, un caractère à la fois.
complexité temporelle :
Dernier cas : O(N)
Dans le pire des cas : O(N*K) (bien sûr, cela peut aussi s'écrire O(N 2 )
Complexité spatiale : O(1)
Pour ouvrir un tableau supplémentaire, placez le dernier k à l'avant du tableau ouvert et placez le premier N - k à l'arrière du tableau.
Complexité temporelle : O(N) (N boucles à travers des éléments de tableau mobiles)
Complexité spatiale : O(N)
Trois temps d'inversion : le premier temps : les premiers N - K sont inversés ; le deuxième temps : les derniers K sont inversés ; le troisième temps : l'ensemble est inversé.
Complexité temporelle : O(N) (un total de 2N éléments sont inversés)
Complexité spatiale : O(1)
Code:
while(left<=right) { int temp = nums[left]; nums[left] = nums[right]; nums[right] = temp; left++; right--; } } void rotate(int* nums, int numsSize, int k){ k%=numsSize; reverse(0,numsSize - k-1,nums); reverse(numsSize - k,numsSize-1,nums); reverse(0,numsSize - 1,nums); } ```