Référence de la note et source de l'image : "Les mathématiques de l'apprentissage profond"
Les mathématiques de l'apprentissage profond (ituring.com.cn)

Table des matières
4.2 Inégalité de Cauchy-Schwarz
4.3 Représentation coordonnée du produit intérieur
4.4 Généralisation des vecteurs
6. Dérivée (fonction à variable unique)
6.2 Dérivées de fonctions fractionnaires et dérivées de fonctions sigmoïdes
6.3 Comment trouver la valeur minimale
7. Dérivées partielles (fonctions multivariables)
7.3 Comment trouver la valeur minimale
7.4 Multiplication des nombres de Lagrange
8.2 Formule dérivée d'une fonction composée d'une variable unique
8.3 Formule dérivée de fonctions composites multivariables
9. Formule approximative de la fonction variable
9.1 Formules approximatives pour les fonctions d'une variable
9.2 Formules approximatives pour les fonctions multivariables
9.3 Représentation vectorielle de formules approchées
10. Méthode de descente de gradient
10.1 Formule de base de la méthode de descente de gradient pour les fonctions à deux variables
10.3 Formule de base de la méthode de descente de gradient pour une fonction à trois variables
La signification de 10,5 η : taux d’apprentissage
11. Problèmes d'optimisation et analyse de régression
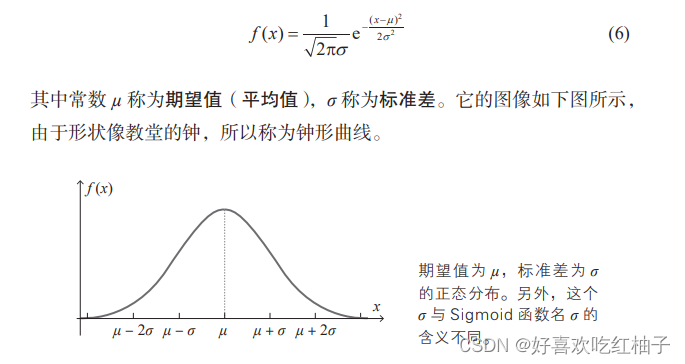
1. Répartition normale
L'utilisation de nombres aléatoires qui suivent une distribution normale lors de la définition des valeurs initiales des poids et des biais donne généralement de bons résultats.
2. Relation de récursion
Les ordinateurs sont bons pour calculer les relations.
Par exemple, regardons le calcul factoriel. La factorielle d'un nombre naturel n est le produit d'entiers de 1 à n, représenté par le symbole n!.
n! = 1×2×3×…×n
Dans la plupart des cas, les gens calculent n ! sur la base de la formule ci-dessus, tandis que les ordinateurs utilisent généralement la relation de récursion suivante pour calculer.
a1 = 1,an + 1 = (n + 1)an
La méthode de rétro-propagation des erreurs utilise cette méthode de calcul dans laquelle les ordinateurs sont doués pour calculer les réseaux de neurones.
3. Symbole ∑

4. Vecteur
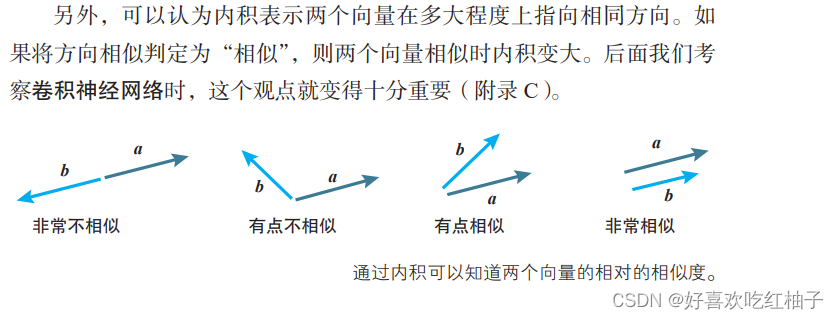
4.1 Produit interne vectoriel
a⋅b = | a | | b |cosθ (θ est l'angle entre a et b)

4.2 Inégalité de Cauchy-Schwarz

La propriété 1 peut être appliquée à la méthode de descente de gradient (la direction opposée du gradient descend le plus rapidement).
4.3 Représentation coordonnée du produit intérieur
Espace bidimensionnel :

Espace tridimensionnel :

4.4 Généralisation des vecteurs

Dans le processus de calcul des réseaux de neurones, la perspective vectorielle est très bénéfique.
Lorsque l'unité neuronale dispose de plusieurs entrées x1, x2,…, xn, elles peuvent être organisées selon les entrées pondérées suivantes.


5. Matrice
5.1 Matrice d'identité
La matrice d'identité, qui est une matrice carrée avec des éléments 1 sur la diagonale et d'autres éléments 0, est généralement représentée par E.
Par exemple, la matrice identité E à 2 lignes et 2 colonnes et 3 lignes et 3 colonnes (appelées matrice identité d'ordre 2 et matrice identité d'ordre 3) sont représentées respectivement comme suit.

La matrice identité est une matrice ayant les mêmes propriétés que 1. Le produit de la matrice identité E et de toute matrice A satisfait la loi commutative suivante.
AE = EA = A
5.2 Produit Hadamard

6. Dérivée (fonction à variable unique)
6.1 Définition des dérivés

6.2 Dérivées de fonctions fractionnaires et dérivées de fonctions sigmoïdes
Dérivées de fonctions fractionnaires :

Dérivé de la fonction sigmoïde :

6.3 Comment trouver la valeur minimale
Lorsque la fonction f(x) prend la valeur minimale à x = a, f'(a) = 0.
7. Dérivées partielles (fonctions multivariables)
7.1 Fonctions multivariables
Une fonction avec plus de deux variables indépendantes est appelée fonction multivariable .
f(x1, x2, …, xn) : Une fonction à n variables indépendantes x1, x2, …, xn.
Il existe des milliers de variables fonctionnelles dans les réseaux de neurones.
7.2 Dérivées partielles
La dérivée par rapport à une variable spécifique est appelée dérivée partielle.

7.3 Comment trouver la valeur minimale

7.4 Multiplication des nombres de Lagrange

8. Règle de chaîne
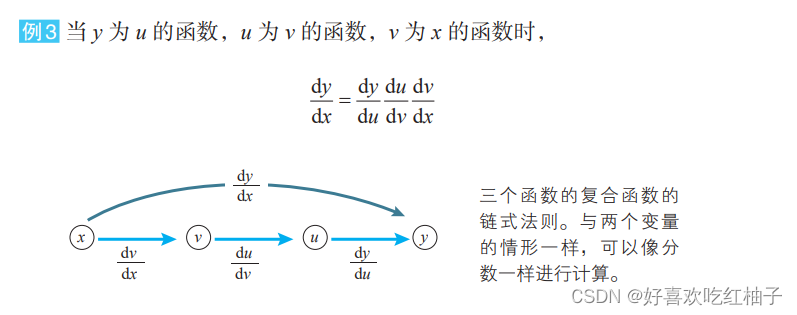
8.1 Fonctions composites
On sait que la fonction y = f(u), lorsque u est exprimé par u = g(x), y en fonction de x peut être exprimé comme une structure imbriquée de la forme y = f(g(x)) (u et x représentent Multivarié). À l’heure actuelle, la fonction f(g(x)) de la structure imbriquée est appelée la fonction composite de f(u) et g(x) .
La fonction dans le réseau neuronal est également une fonction composite typique.

8.2 Formule dérivée d'une fonction composée d'une variable unique

8.3 Formule dérivée de fonctions composites multivariables
z = f(u,v), trouvez la dérivée partielle de la variable x :
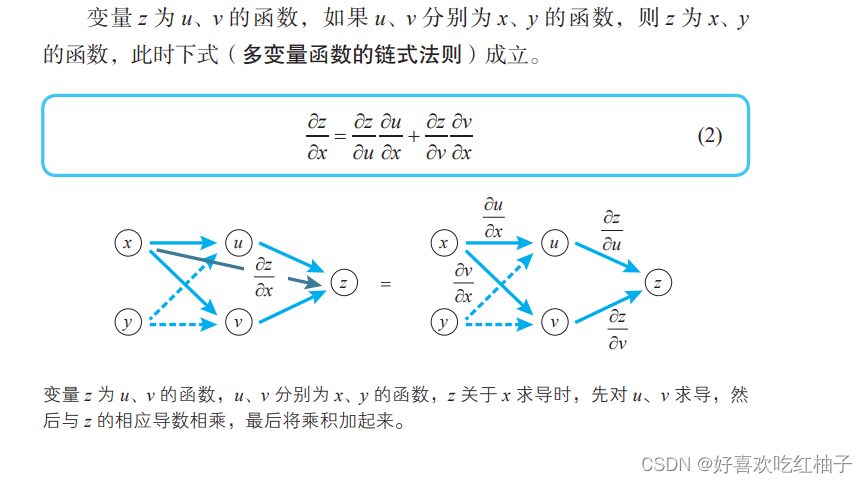
Trouvez la dérivée partielle de la variable y :

C = f(u,v,w) , trouvez la dérivée partielle de u : (Idem pour v et w)

9. Formule approximative de la fonction variable
La méthode de descente de gradient est une méthode représentative pour déterminer les réseaux de neurones. Lors de l'application de la méthode de descente de gradient, une formule approximative pour une fonction multivariable doit être utilisée.
9.1 Formules approximatives pour les fonctions d'une variable

9.2 Formules approximatives pour les fonctions multivariables
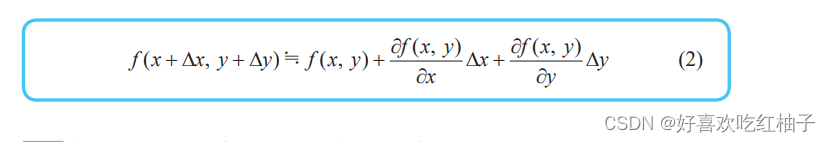
Simplifiez la formule et utilisez la lettre z pour représenter le changement de fonction z = f(x, y) lorsque x et y changent de Δx et Δy :

La version simplifiée de la formule approchée est la suivante. De la même manière, la formule approchée d'une fonction à trois variables peut également être exprimée de cette manière.

9.3 Représentation vectorielle de formules approchées
La formule approximative peut être exprimée comme le produit scalaire des deux vecteurs suivants ∇ z⋅Δ x.

10. Méthode de descente de gradient
La méthode de descente de gradient est la méthode la plus couramment utilisée pour trouver la valeur minimale d'une fonction, c'est-à-dire utiliser la direction du gradient négatif pour déterminer la nouvelle direction de recherche pour chaque itération, afin que chaque itération puisse réduire progressivement la fonction objectif à optimiser. .
10.1 Formule de base de la méthode de descente de gradient pour les fonctions à deux variables
Le processus de dérivation
Lorsque x change Δx et y change Δy, le changement Δz de la fonction f (x, y) est :
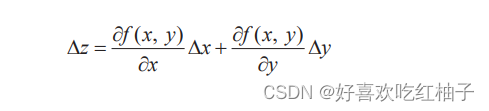
La formule ci-dessus peut être exprimée sous la forme du produit scalaire de deux vecteurs a et b.


On sait que lorsque la direction de b est opposée à celle de a, le produit scalaire ab.b prend la valeur minimale. Autrement dit, lorsque le vecteur b satisfait b= - ka (k est une constante positive), le produit scalaire a·b prend la valeur minimale.
C'est-à-dire que lorsque les directions des deux vecteurs a et b sont exactement opposées, Δz peut être minimisé (c'est-à-dire diminuer le plus rapidement)

De là, nous pouvons obtenir la formule de base de la méthode de descente de gradient d’une fonction à deux variables.
Lors du déplacement du point (x, y) au point (x + Δx, y + Δy), lorsque :

La fonction z = f (x, y) diminue le plus rapidement.
10.2 Dégradé
Le gradient est un vecteur (vecteur) , ce qui signifie que la dérivée directionnelle d'une certaine fonction à ce point prend la valeur maximale dans cette direction, c'est-à-dire que la fonction change le plus rapidement dans cette direction (la direction du gradient) à ce point et a le taux de changement le plus élevé (c'est le module du gradient).

10.3 Formule de base de la méthode de descente de gradient pour une fonction à trois variables
La formule de base de la méthode de descente de gradient pour les fonctions à deux variables peut être facilement étendue à des situations comportant plus de trois variables. Lorsque la fonction f est constituée de n variables indépendantes x1, x2,…, xn, la formule de base de trois variables peut être généralisée.

10.4 Opérateur hamiltonien


La signification de 10,5 η : taux d’apprentissage
Dans le monde des réseaux de neurones, l'êta est appelé taux d'apprentissage . Il n'existe pas de norme claire pour sa méthode de détermination, et la valeur appropriée ne peut être trouvée que par essais et erreurs.

11. Problèmes d'optimisation et analyse de régression
En termes d'optimisation, la somme des erreurs peut être appelée « fonction d'erreur », « fonction de perte », « fonction de coût », etc. La méthode d'optimisation utilisant la somme des erreurs quadratiques est appelée méthode des moindres carrés .