Aujourd'hui, nous allons parler de quelque chose de purement technique. Cette chose est la base et nous ne pouvons pas l'expliquer plus tard. Dans le domaine de l'apprentissage automatique, nous pouvons empêcher le surapprentissage grâce à la régularisation. Qu'est-ce que la régularisation ? Les plus courants sont la régression de crête, la régression LASSO et le réseau élastique.
Tout d’abord, parlons de ce qu’est le surapprentissage ? Regardons l'image ci-dessous
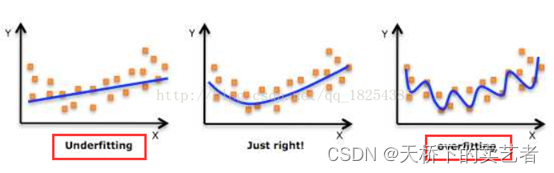
Le 1 de gauche est appelé sous-ajustement, celui du milieu est mieux ajusté et le 1 de droite est surajustement, car il accorde trop d'attention à la zone locale, ce qui rend la limite du graphique trop compliquée et nous ne pouvons pas ajuster pour le plaisir d'ajuster. , comme le droit 1 La situation doit très bien s'adapter à ces données, mais elle ne fonctionnera pas dans d'autres données, donc le surajustement n'a aucune utilité pratique. L'image suivante classe également les données de la même manière :
Figure 2 :
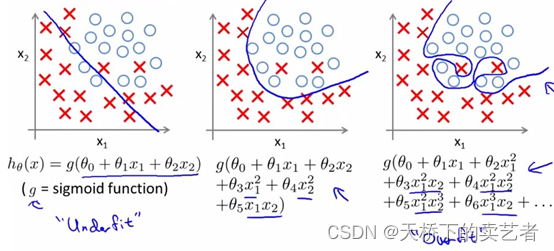
Nous pouvons voir à quel point l'algorithme sur le côté droit de l'image ci-dessus est compliqué afin d'augmenter le degré d'ajustement. Le but de la régularisation est de supprimer les algorithmes complexes pour réaliser un surajustement. Ceci est principalement réalisé en compressant les coefficients du modèle via une fonction de pénalité. Avant cela, parlons de la méthode des moindres carrés et de la fonction de perte.
La méthode des moindres carrés est largement utilisée en statistiques et en apprentissage automatique.
Il y a 4 points rouges dans l'image ci-dessous. Nous devons adapter la tendance de ces 4 points. Ensuite, nous devons trouver une ligne. En supposant que nous l'avons trouvée, il s'agit de la ligne bleue dans l'image ci-dessous. Ensuite, le Y de la position du point rouge est la valeur réelle de Y, et la valeur Y de la ligne bleue sur le même axe X est la valeur prédite de Y. C'est compréhensible. La différence entre la valeur réelle de Y et la valeur prédite de Y est notre erreur, également appelée résidu en statistique, qui est la partie verte.
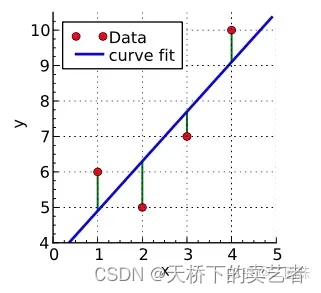
Alors, comment trouver la ligne la plus appropriée pour correspondre à la tendance de 4 points, qui est
Y1 (valeur réelle) - Y1 (valeur d'erreur) + Y2 (valeur réelle) - Y2 (valeur d'erreur) + Y3 (valeur réelle) - Quand Y3 (valeur d'erreur) + Y4 (valeur réelle) - Y4 (valeur d'erreur) est égal au minimum.
C’est à ce moment-là que la somme des longueurs de toutes les lignes vertes est la plus petite. Parce que parfois la valeur réelle moins la valeur moyenne peut avoir une valeur négative, nous mettons donc leurs différences au carré puis les additionnons, ce qui est
(Y1 (valeur réelle) - Y1 (valeur d'erreur)) 2+ (Y2 (valeur réelle)) -Y2 (valeur d'erreur)) 2+ (Y3 (valeur réelle)-Y3 (valeur d'erreur)) 2+ (Y4 (valeur réelle)-Y4 (valeur d'erreur)) 2 Dans les statistiques de données, nous pouvons utiliser Y_i pour représenter Y
Le valeur réelle de
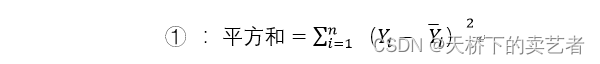
En apprentissage automatique, la fonction combinée à des paramètres optimisés est appelée fonction de perte. Dans cet exemple, notre fonction somme des carrés est la fonction de perte, qui est en fait la fonction qui minimise l’erreur. Nous trouvons une droite qui minimise la somme de tous les carrés, qui est notre droite d’ajustement la plus appropriée.
La situation actuelle est relativement simple. Lorsqu'elle est compliquée, comme dans la situation de droite sur la figure 2, un surajustement peut se produire afin de minimiser la fonction de perte. Les méthodes de régularisation courantes que nous utilisons pour éviter le surajustement incluent la régression de crête, la régression LASSO et les réseaux élastiques. Parlons maintenant du retour en ligne de Xialing.
La régression Ridge ajoute une fonction de pénalité, appelée norme L2, à la fonction de perte ① à l'instant, qui est accumulée après le carré de β, puis multipliée par le coefficient λ. Il convient de noter ici que le coefficient n’inclut pas ici le terme d’origine.
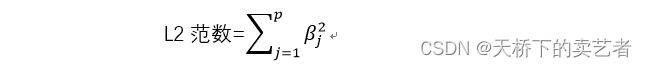
Après avoir ajouté la norme L2, la formule de la fonction de perte est la suivante :
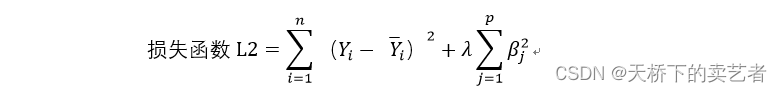
On voit qu'après avoir ajouté le paramètre λ à la norme L2, s'il y a beaucoup de β dans le modèle, la valeur augmentera après l'accumulation du carré de β. À ce stade, λ peut compresser la somme accumulée de β au carré et optimiser notre fonction de perte. La fonction λ est un hyperparamètre et ne peut pas être estimée à partir des données. Un λ optimal ne peut être obtenu que par des itérations continues de validation croisée du modèle. Dans notre article précédent "Vous apprendre étape par étape comment utiliser le langage R pour faire une régression LASSO" nous pouvons voir l'image suivante (l'image ci-dessous est générée par la régression LASSO, mais le principe est le même). En fait, un λ garde devenir plus grand,
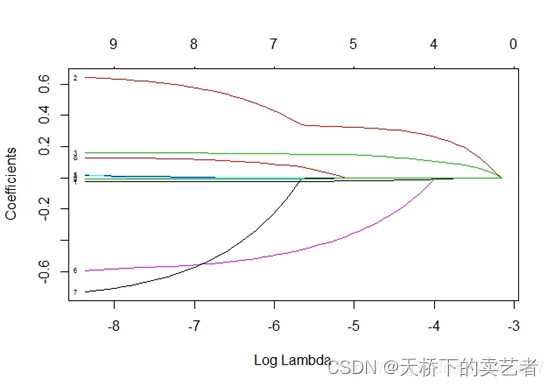
validé de manière croisée, puis le meilleur résultat est obtenu.Un processus de performance optimale, dans lequel les coefficients peuvent être vus comme compressés.
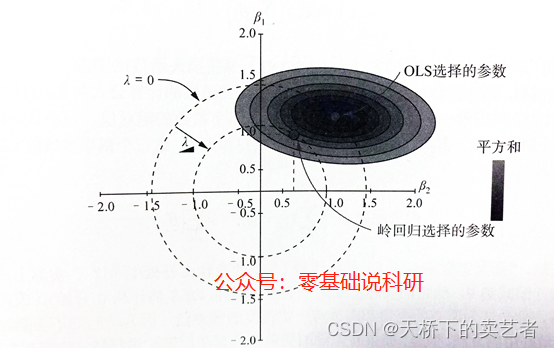
À partir de la figure ci-dessus, nous pouvons constater que lorsque λ = 0, les coefficients de β1 et β2 sont tous deux égaux à 1,5. De cette façon, lorsque λ est davantage comprimé dans le cercle, les coefficients de β1 et β2 deviennent plus petits et le coefficient de β2 au point sélectionné par la régression de crête a été compressé à 0,6, donc l'utilisation de la régression de crête évite un surajustement du modèle d'entraînement aux données.
Parlons ensuite de la régression LASSO. Quelle est la différence entre celle-ci et la régression Ridge ? La régression Ridge utilise la norme L2, tandis que LASSO utilise la norme L1. La formule est la suivante :
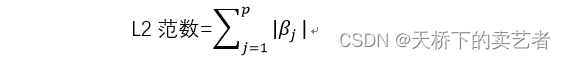
La norme de la régression de crête est l'accumulation de carrés de coefficients β, tandis que LASSO est l'accumulation des valeurs absolues des coefficients β. Voici la formule de la fonction de perte de régression LASSO. La question est donc de savoir quelle est la différence entre ces deux fonctions
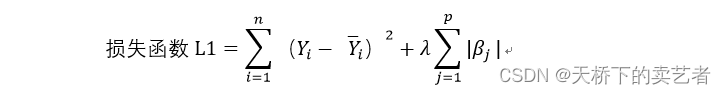
? La régression Ridge compressera les coefficients, mais les coefficients ne seront pas compressés à 0, mais la régression LASSO peut compresser les coefficients à 0. Cela peut nous aider à filtrer les indicateurs.
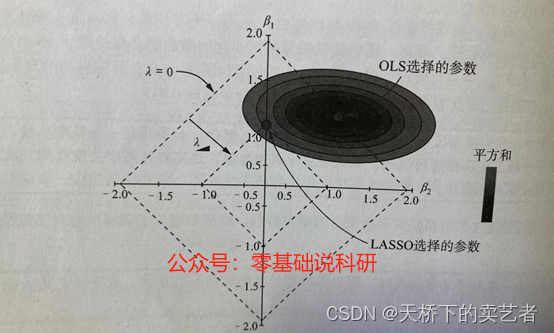
Nous pouvons voir que la fonction de pénalité de la régression Ridge est circulaire, tandis que la fonction de pénalité de la régression LASSO est en forme de losange. Dans la même régression Lambda Ridge, le coefficient de β2 est de 0,6, tandis que le coefficient de β2 dans la régression LASSO est de 0, indiquant que β2 a été supprimé.
Enfin, parlons de ce qu'est un réseau élastique. Le réseau élastique est une combinaison packagée de régression de crête et de régression LASSO. Sa formule est la suivante : On peut voir que le réseau élastique introduit l'hyperparamètre α. Lorsque α est égal à 0, le réseau
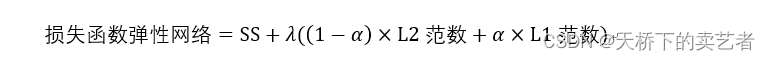
élastique réseau élastique Il est égal à la régression ridge. Lorsque α est égal à 1, il est égal à la régression LASSO. Par conséquent, il présente les avantages de la régression ridge et de la régression LASSO et est plus populaire.
À ce stade, la théorie est pratiquement terminée et parler de théorie prend vraiment beaucoup de temps. Revenons sur l'article suivant en combinant le package glmnet avec mon article " Vous apprendre étape par étape à utiliser le langage R pour effectuer une régression LASSO ". Jetons un coup d'œil à l'explication des paramètres
de la fonction glmnet dans le glmnet emballer.
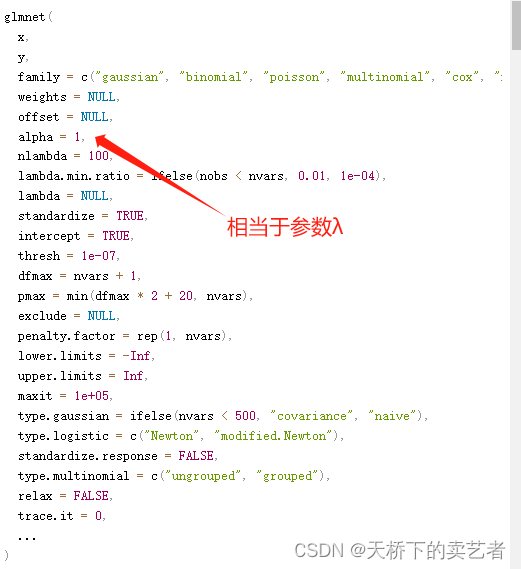
Cela dépend principalement du paramètre alpha. 1 est le lasso et 0 est la pénalité de crête. Est-il très similaire à notre réseau élastique ?

Jetons ensuite un œil au graphique du coefficient de compression généré dans LASSO.
cvfit=cv.glmnet(x,y)
plot(cvfit)
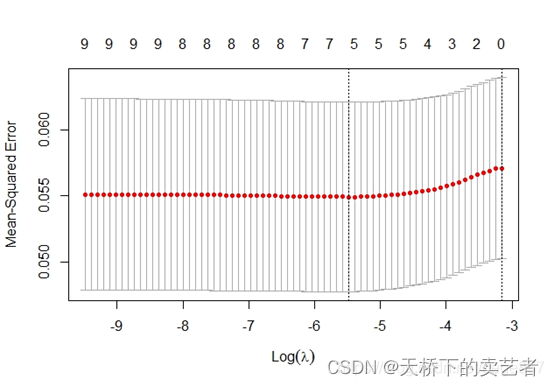
On peut voir que la fonction cv.glmnet génère un tracé du MSE de ce changement lambda,

On voit que la fonction cv.glmnet est une fonction de validation croisée, elle calcule le MSE grâce à la valeur lambda fournie et obtient finalement une solution optimale. Cela confirme ce que nous disions ci-dessus.
Enfin, pour résumer, nous avons aujourd'hui une introduction préliminaire à la régression ridge, à la régression LASSO, au réseau élastique et à la fonction de perte. La fonction de perte est une partie importante de l'apprentissage automatique. Il n'y a aucun moyen d'en parler sans le mentionner. Lorsque nous aurons le temps plus tard, nous présenterons comment dériver manuellement les résultats de la régression logistique ou de la régression linéaire en langage R. Après avoir compris le principe et comment la régression génère des résultats, de nombreux problèmes dans R peuvent être résolus facilement, comme l'erreur suivante : 1 : glm.fit : l'algorithme n'agrège pas 2 : glm.fit : la probabilité d'ajustement est calculée comme étant un valeur de zéro ou un
Tout cela est dû au fait que le modèle ne converge pas, parlons-en quand nous aurons le temps.