1. Descriptif
Dans cette série , nous apprendrons à écrire des algorithmes d'apprentissage en profondeur indispensables tels que les convolutions, la rétropropagation, les fonctions d'activation, les optimiseurs, les réseaux de neurones profonds, etc., en utilisant uniquement du C++ simple et moderne.
Dans cette histoire, nous présenterons l'ajustement des noyaux de convolution 2D aux données en introduisant l'algorithme de descente de gradient . Nous allons tout coder en C++ et Eigen modernes en utilisant des convolutions et le concept de fonction de coût introduit dans l'histoire précédente .

Cette histoire est : Gradient Descent en C++, voir d'autres histoires :
0 — Principes de base de la programmation d'apprentissage en profondeur C++ moderne
1 — Codage de la convolution 2D en C++
2 — Fonction de coût utilisant Lambda
... et bien d'autres à venir.
2. L'approximation de fonctions comme problème d'optimisation
Si vous avez lu nos exposés précédents, vous savez déjà que dans l'apprentissage automatique, nous nous concentrons la plupart du temps sur l'utilisation de données pour trouver des approximations de fonctions.
Habituellement, nous obtenons une approximation de la fonction en trouvant les coefficients qui minimisent la valeur du coût . Par conséquent, notre problème d'approximation est transformé en un problème d'optimisation, où nous essayons de minimiser la valeur de la fonction de coût.
3. Fonction de coût et descente de gradient
La fonction de coût calcule le coût d' approximation de la fonction objectif F(X ) à l'aide de la fonction H(X ) . Par exemple, si H(X) est une convolution entre l'entrée X et le noyau k , la fonction de coût MSE est donnée par :
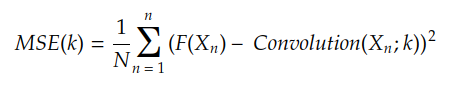
On fait habituellement Y n = F (Xn), le résultat est :
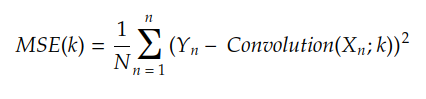
MSE est l'erreur quadratique moyenne et est la fonction de coût introduite dans l'histoire précédente
Par conséquent, notre objectif est de trouver la valeur du noyau k m qui minimise MSE(k) . L'algorithme le plus basique (mais le plus puissant) pour trouver k m est la descente de gradient.
La descente de gradient utilise le gradient de la fonction de coût pour trouver le coût minimum. Pour comprendre ce qu'est un gradient, parlons des surfaces de coût.
4. Dessinez la surface de coût
Pour une meilleure compréhension, supposons temporairement que le noyau se compose de seulement deux coefficients. Si nous traçons la valeur de MSE(k) pour chaque combinaison possible , nous obtenons une surface comme celle-ci :k[k00, k01][k00, k01]

En chaque point, la surface a une inclinaison sur l'axe 0k₀₀ et une autre inclinaison sur l' axe 0k₀₁ :(k00, k01, MSE(k00, k01))
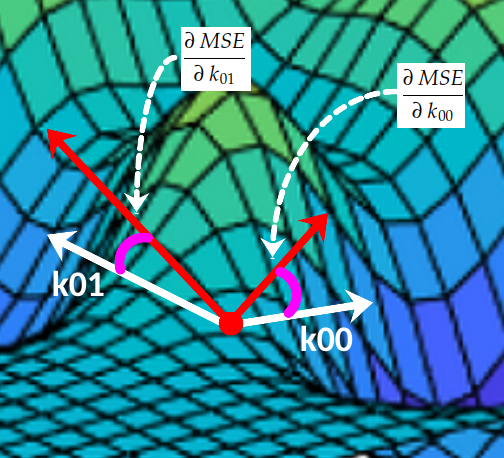
Dérivée partielle
Ces deux pentes sont les dérivées partielles de la courbe MSE par rapport aux axes O k₀₀ et O k₀₁ , respectivement . En calcul, nous utilisons beaucoup la notation ∂ pour désigner les dérivées partielles :
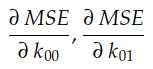
Ces deux dérivées partielles constituent ensemble le gradient de l'EQM par rapport aux axes O k₀₀ et O k₀₁ . Ce gradient est utilisé pour piloter l'exécution de l'algorithme de descente de gradient comme suit :
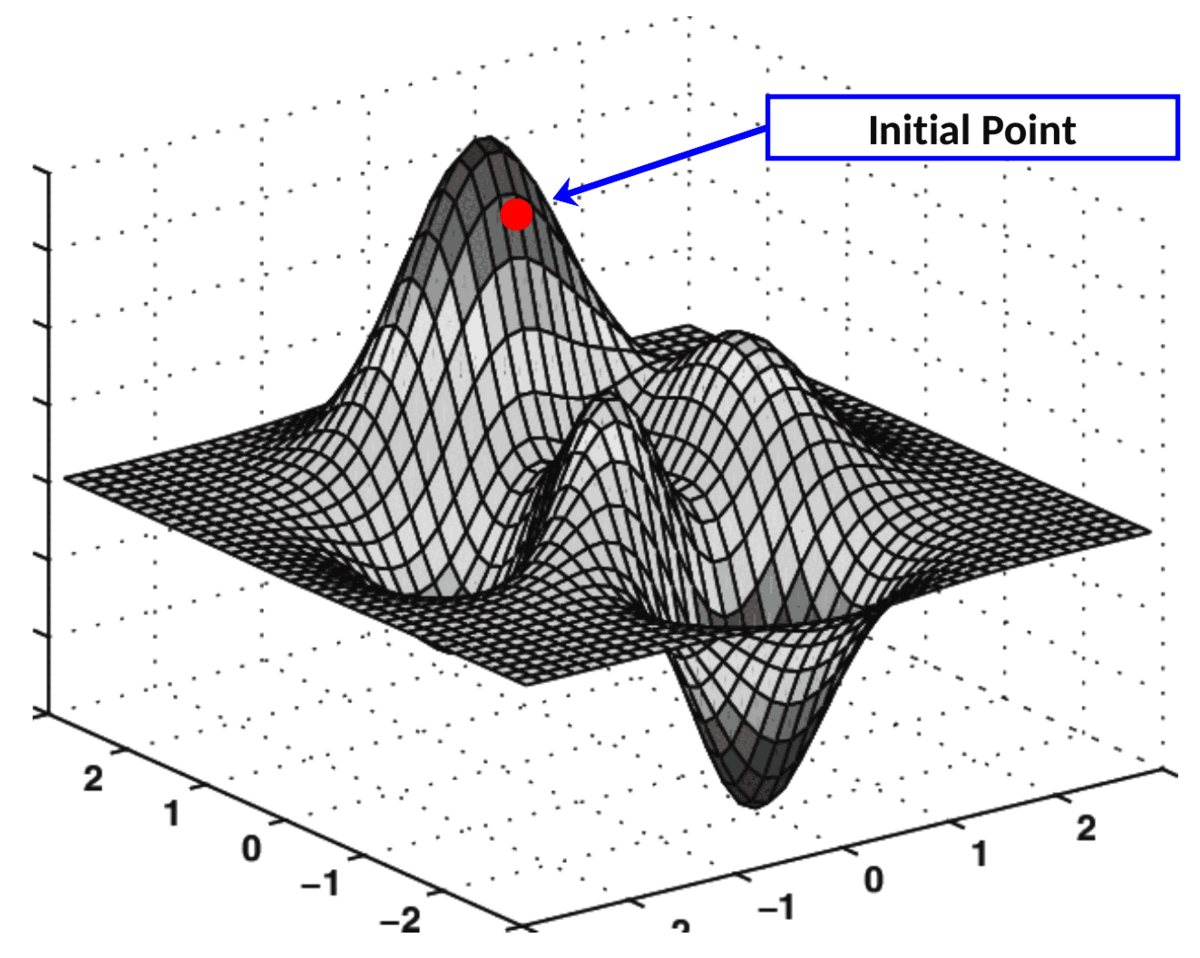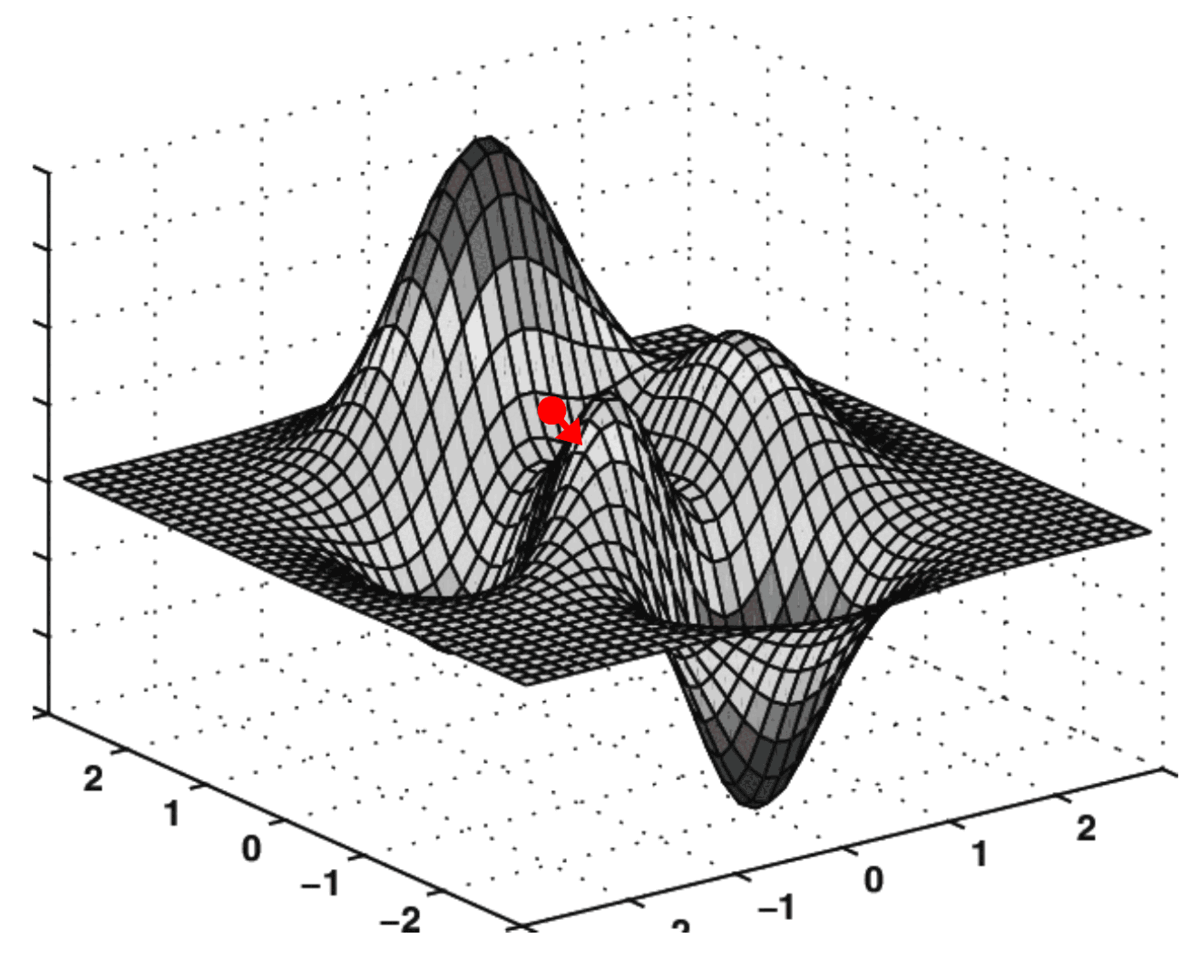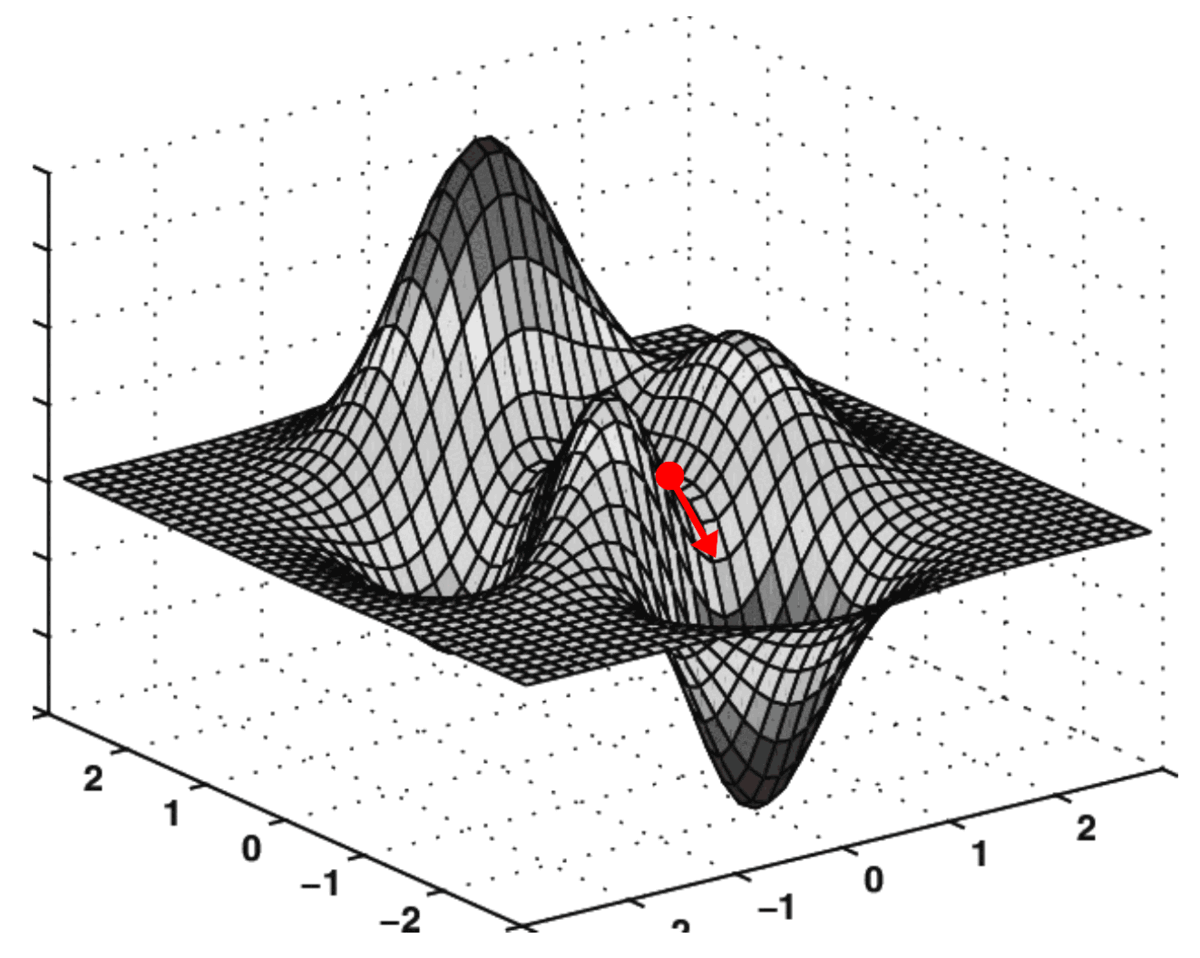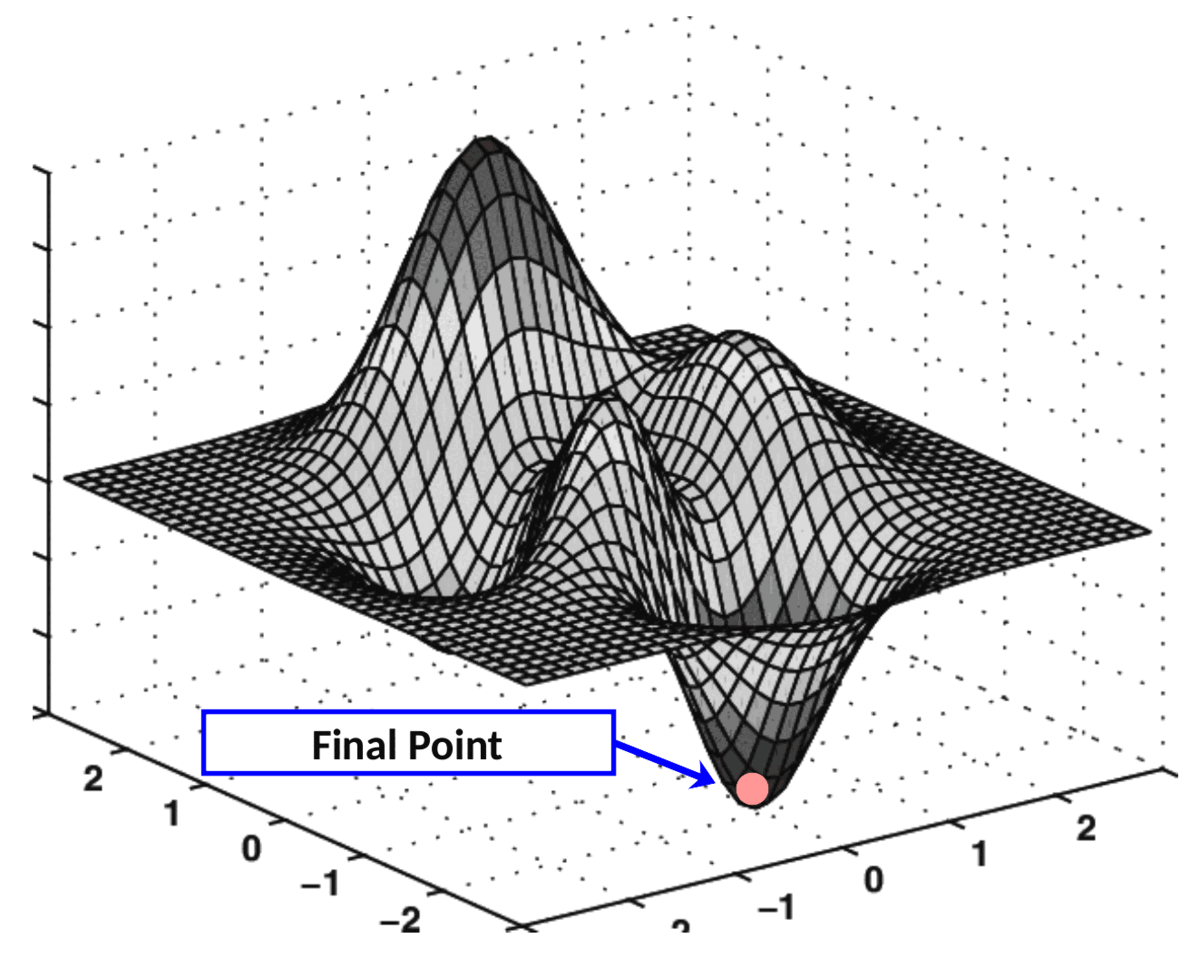
Applications pratiques de la descente de gradient
L'algorithme qui effectue cette "navigation" sur une surface de coût est appelé descente de gradient.
5. Descente en dégradé
Le pseudocode de descente de gradient est décrit comme suit :
gradient_descent:
initialize k, learning_rate, epoch = 1
repeat
k = k - learning_rate x ∇Cost(k)
until epoch <= max_epoch
return kLa valeur de learning_rate x ∇Cost(k) est souvent appelée mise à jour du poids . On peut restaurer le comportement de descente de gradient avec :
for each iteration:
calculate the weight update
subtract it from the parameter kComme son nom l'indique, Cost(k) est la fonction de coût pour la configuration k . Le but de la descente de gradient est de trouver la valeur de k qui minimise le coût (k) .
learning_rate est généralement un scalaire comme 0,1, 0,01, 0,001 ou plus. Cette valeur contrôle la taille du pas pendant l'optimisation.
L'algorithme boucle max_epoch fois. Parfois, nous arrêtons l'algorithme plus tôt, c'est-à-dire même si epoch < max_epoch , dans le cas où Cost(k) est trop petit.
Nous nous référons généralement à des paramètres tels que learning_rate et max_epoch par les noms d'hyperparamètres .
Pour implémenter la descente de gradient, la dernière chose que nous devons savoir est de savoir comment calculer le gradient de C(k) . Heureusement, dans le cas où la fonction de coût est MSE, trouver ∇Cost(k) est trivial, comme mentionné précédemment.
6. Trouver le gradient MSE
Jusqu'ici nous avons vu que les composantes du gradient sont les pentes de la surface de coût pour chaque axe 0 k ij . On voit aussi que le gradient de MSE ( k ) par rapport au coefficient j- de chaque i , noyau k est donné par :
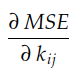
Rappelons que MSE(k) est donné par :
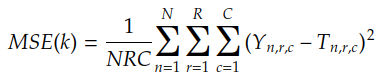
où n est l'indice de chaque paire ( Y n, T n) et r & c sont les indices des coefficients de la matrice de sortie :
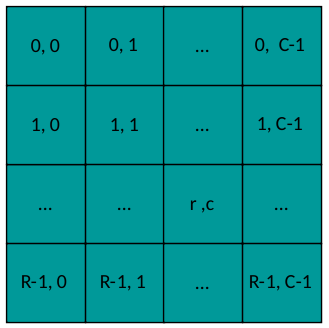
mise en page de sortie
En utilisant la règle de chaîne et la règle de combinaison linéaire, nous pouvons trouver le gradient MSE de la manière suivante :
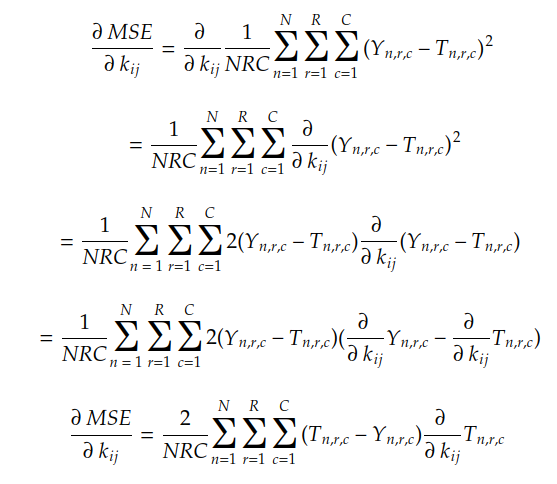
Puisque les valeurs de N , R , C , Y n et T n sont connues, il suffit de calculer la dérivée partielle de chaque coefficient de T n par rapport au coefficient kij . Dans le cas de la convolution avec bourrage P, cette dérivée est donnée par :
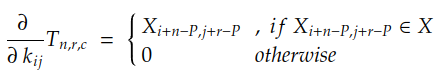
Si nous développons la somme de r et c , nous pouvons trouver que le gradient est donné par :
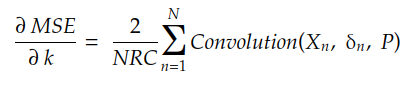
où δn est la matrice :
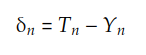
Le code suivant fait cela :
auto gradient = [](const std::vector<Matrix> &xs, std::vector<Matrix> &ys, std::vector<Matrix> &ts, const int padding)
{
const int N = xs.size();
const int R = xs[0].rows();
const int C = xs[0].cols();
const int result_rows = xs[0].rows() - ys[0].rows() + 2 * padding + 1;
const int result_cols = xs[0].cols() - ys[0].cols() + 2 * padding + 1;
Matrix result = Matrix::Zero(result_rows, result_cols);
for (int n = 0; n < N; ++n) {
const auto &X = xs[n];
const auto &Y = ys[n];
const auto &T = ts[n];
Matrix delta = T - Y;
Matrix update = Convolution2D(X, delta, padding);
result = result + update;
}
result *= 2.0/(R * C);
return result;
};Maintenant que nous savons comment obtenir des gradients, implémentons l'algorithme de descente de gradient.
7. Encodage de la descente de gradient
Enfin, notre code de descente de gradient est ici :
auto gradient_descent = [](Matrix &kernel, Dataset &dataset, const double learning_rate, const int MAX_EPOCHS)
{
std::vector<double> losses; losses.reserve(MAX_EPOCHS);
const int padding = kernel.rows() / 2;
const int N = dataset.size();
std::vector<Matrix> xs; xs.reserve(N);
std::vector<Matrix> ys; ys.reserve(N);
std::vector<Matrix> ts; ts.reserve(N);
int epoch = 0;
while (epoch < MAX_EPOCHS)
{
xs.clear(); ys.clear(); ts.clear();
for (auto &instance : dataset) {
const auto & X = instance.first;
const auto & Y = instance.second;
const auto T = Convolution2D(X, kernel, padding);
xs.push_back(X);
ys.push_back(Y);
ts.push_back(T);
}
losses.push_back(MSE(ys, ts));
auto grad = gradient(xs, ys, ts, padding);
auto update = grad * learning_rate;
kernel -= update;
epoch++;
}
return losses;
};C'est le code de base. Nous pouvons l'améliorer de plusieurs façons, par exemple :
- en utilisant la perte de chaque instance pour mettre à jour le noyau. C'est ce qu'on appelle la descente de gradient stochastique (SGD) , qui est très utile dans les scénarios du monde réel ;
- le regroupement des instances en batch et la mise à jour du noyau après chaque batch, que l'on appelle Minibatch ;
- Utilisez un calendrier de taux d'apprentissage pour réduire le taux d'apprentissage à travers les époques ;
- Dans cette ligne, nous pouvons connecter un optimiseur tel que Momentum , RMSProp ou Adam. Nous discuterons des optimiseurs dans la prochaine histoire ;
kernel -= update; - Apportez un ensemble de validation ou utilisez une architecture de validation croisée ;
- Remplacement des boucles imbriquées par la vectorisation pour les performances et l'utilisation du processeur (comme mentionné dans l'histoire précédente) ;
for(auto &instance: dataset) - Ajoutez des rappels et des crochets pour personnaliser plus facilement notre boucle de formation.
Nous pouvons oublier ces améliorations pour un moment. Maintenant, l'accent est mis sur la compréhension de la façon dont les gradients sont utilisés pour mettre à jour les paramètres (les noyaux dans notre cas). Il s'agit d'un concept fondamental et central de l'apprentissage automatique aujourd'hui, et d'un facteur clé pour faire avancer des sujets plus avancés.
Mettons cela en action avec une expérience illustrative pour voir comment ce code fonctionne.
Huit, l'expérience réelle : réparer le détecteur de bord Sobel
Dans la dernière histoire, nous avons appris que nous pouvons appliquer un filtre de Sobel Gx pour détecter les bords verticaux :
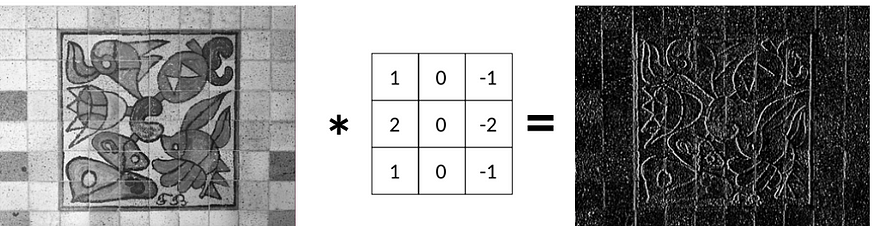
Maintenant, la question est : compte tenu de l'image d'origine et de l'image des contours, a-t-on réussi à récupérer le filtre de Sobel Gx ?

En d'autres termes, pouvons-nous ajuster un noyau étant donné une entrée X et une sortie attendue Y ?
La réponse est oui, nous utiliserons la descente de gradient pour ce faire.
9. Charger et préparer les données
Tout d'abord, nous lisons quelques images d'un dossier à l'aide d'OpenCV. Nous leur appliquons le filtre Gx et les stockons par paires dans notre objet dataset :
auto load_dataset = [](std::string data_folder, const int padding) {
Dataset dataset;
std::vector<std::string> files;
for (const auto & entry : fs::directory_iterator(data_folder)) {
Mat image = cv::imread(data_folder + entry.path().c_str(), cv::IMREAD_GRAYSCALE);
Mat formatted_image = resize_image(image, 640, 640);
Matrix X;
cv::cv2eigen(formatted_image, X);
X /= 255.;
auto Y = Convolution2D(X, Sobel.Gx, padding);
auto pair = std::make_pair(X, Y);
dataset.push_back(pair);
}
return dataset;
};
auto dataset = load_dataset("../images/");Nous utilisons l'utilitaire d'assistance .resize_image pour formater chaque image d'entrée pour qu'elle tienne sur une grille 640x640

Centrez chaque image dans une grille noire 640x640 comme indiqué ci-dessus sans étirer l'image en la redimensionnant simplement. redimensionner_image
Nous utilisons le filtre Gx pour générer la sortie de vérité terrain Y pour chaque image. Maintenant, nous pouvons oublier ce filtre. Nous allons le récupérer à partir des données en utilisant la descente de gradient et la convolution 2D.
10. Exécutez l'expérience
En connectant toutes les pièces, on peut enfin voir la formation effectuer :
int main() {
const int padding = 1;
auto dataset = load_dataset("../images/", padding);
const int MAX_EPOCHS = 1000;
const double learning_rate = 0.1;
auto history = gradient_descent(kernel, dataset, learning_rate, MAX_EPOCHS);
std::cout << "Original kernel is:\n\n" << std::fixed << std::setprecision(2) << Sobel.Gx << "\n\n";
std::cout << "Trained kernel is:\n\n" << std::fixed << std::setprecision(2) << kernel << "\n\n";
plot_performance(history);
return 0;
}La séquence suivante illustre le processus d'ajustement :

Au début, le noyau est rempli de nombres aléatoires. Par conséquent, à la première époque, l'image de sortie est généralement une sortie noire.
Cependant, après quelques époques, la descente de gradient commence à ajuster le noyau au minimum global.
Enfin, à la dernière époque, la sortie est presque égale à la vérité terrain. À ce stade, la valeur de perte se déplace asymptotiquement vers la valeur la plus basse. Vérifions les performances de perte au fil du temps :
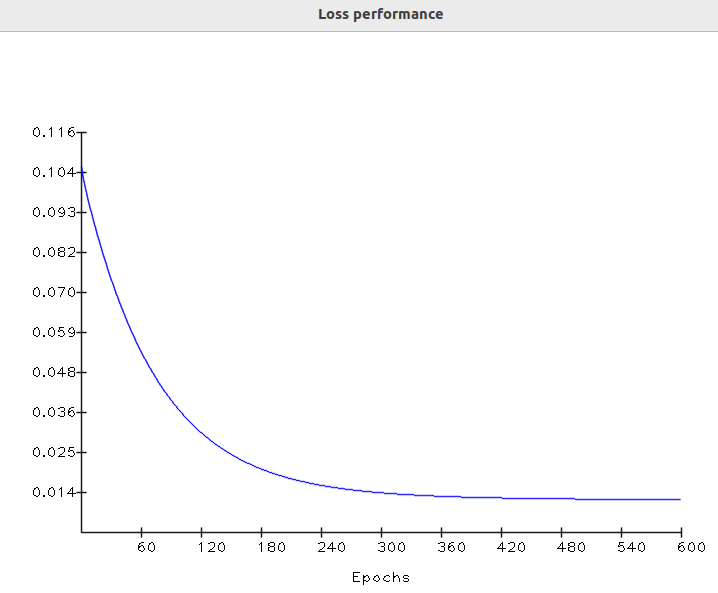
performances d'entraînement
Cette forme de courbe de perte est très courante en apprentissage automatique. Il s'avère qu'à la première époque, les paramètres étaient essentiellement des valeurs aléatoires. Il en résulte une perte initiale élevée :

Représentation algorithmique de la recherche sur les surfaces de coût
Dans la dernière époque, la descente de gradient fait enfin son travail, ajustant le noyau à une valeur appropriée, ce qui fait converger la perte vers un minimum.
Nous pouvons maintenant comparer le noyau appris avec le filtre Gx Sobel d'origine :
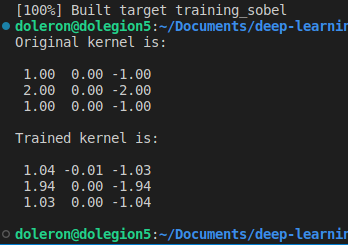
Comme nous nous y attendions, le noyau appris est très proche du noyau d'origine. Notez que cette différence peut encore être plus petite si nous entraînons le noyau sur plus d'époques (et utilisons un taux d'apprentissage plus petit).
Le code utilisé pour former ce noyau peut être trouvé dans ce référentiel .
11. À propos de la différenciation etautodiff
Dans cette histoire, nous utilisons des règles de calcul communes pour trouver les dérivées partielles MSE. Cependant, trouver la dérivée algébrique pour une fonction de coût complexe donnée peut être difficile dans certains cas. Heureusement, les cadres d'apprentissage automatique modernes offrent une fonctionnalité magique appelée différenciation automatique ou simplement.autodiff
autodiffGardez une trace de chaque opération arithmétique de base (telle que l'addition ou la multiplication), en leur appliquant la règle de la chaîne pour trouver les dérivées partielles. Ainsi, lors de l'utilisation de , nous n'avons pas besoin de formules algébriques pour calculer les dérivées partielles, ni même les implémenter directement.autodiff
Comme nous utilisons ici des formules de coût simples et bien connues, il n'est pas nécessaire d'utiliser manuellement ou même de résoudre des différentiels complexes.autodiff
Couvrir plus en détail les dérivées, les dérivées partielles et la différenciation automatique mérite une nouvelle histoire !
12.Conclusion
Dans cette histoire, nous avons appris à utiliser les gradients pour ajuster les noyaux aux données. Nous avons introduit la descente de gradient, qui est simple, puissante et la base pour dériver des algorithmes plus complexes tels que la rétropropagation. Nous avons également réalisé une expérience pratique utilisant la descente de gradient pour récupérer le filtre de Sobel à partir des données.
livre de référence
Apprentissage automatique, Mitchell
Cálculo 3, Geraldo Ávila (portugais brésilien)
Réseaux de neurones : principes de base complets, Haykin
Classification des modèles, Duda
Vision par ordinateur : algorithmes et applications, Szeliski.