[Structure de données C/C++] Explication de base et conceptuelle de l'arborescence et de l'arborescence binaire

Arborescence et concepts

arborescence

Définition de l'arbre : L'arbre est une structure de données non linéaire , qui est un ensemble de relations hiérarchiques composé de n (n>=0) nœuds finis. On l'appelle un arbre parce qu'il ressemble à un arbre à l'envers, ce qui signifie qu'il a les racines pointant vers le haut et les feuilles pointant vers le bas.

La structure de l'arbre a la définition suivante :

• Il existe un nœud spécial, appelé le nœud racine , le nœud racine n'a pas de nœuds prédécesseurs

• Hormis le nœud racine, les autres nœuds sont divisés en M (M>0) ensembles disjoints entre eux $J_{}、T_{}、......、T_{}$, où chaque ensemble $J_{}$(1<= i <= m) est un autre sous-arbre avec une structure similaire à un arbre. Le nœud racine de chaque sous-arborescence a un et un seul prédécesseur, et peut avoir zéro ou plusieurs successeurs.

• Les arbres sont définis de manière récursive.

• Dans une structure arborescente, il ne peut y avoir d'intersection entre sous-arbres, sinon ce n'est pas une structure arborescente.

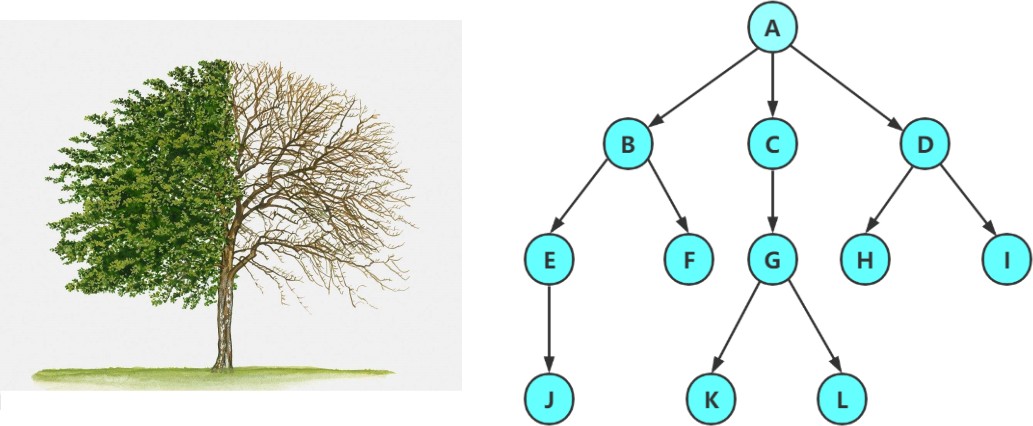
• Tout arbre sera divisé en racines et sous-arbres, et chaque nœud racine de l'arbre est son sous-arbre

  Par exemple, dans la figure de droite ci-dessous, A est le nœud racine et son sous-arbre est BCD ; de même, B est le nœud racine et son sous-arbre est EF. Et ainsi de suite...

Concepts de base des arbres

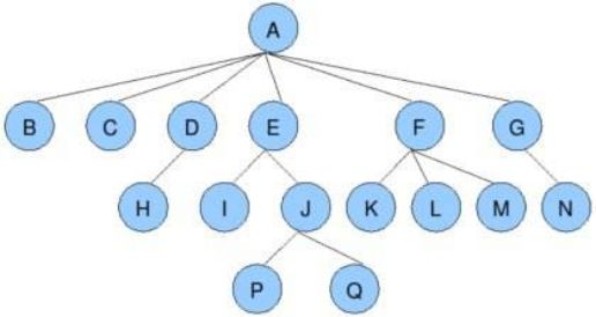
• Degré d'un nœud : le nombre de sous-arbres contenus dans un nœud est appelé le degré du nœud ; comme le montre la figure ci-dessus : A vaut 6, B vaut 0, D vaut 1 et F vaut 3 ;
• Nœud feuille (nœud terminal) : un nœud avec un degré de 0 est appelé un nœud feuille ; comme le montre la figure ci-dessus : les nœuds tels que B, C, H, I, etc. n'ont pas de sous-arbres en dessous d'eux et le degré est 0 .
• Nœud de branche (nœud non terminal) : un nœud dont le degré n'est pas 0 est un nœud de branche ; comme le montre la figure ci-dessus : D, E, F, G... et les autres nœuds ont tous des sous-arbres et un degré !=0, qui est un nœud de branche ;
• Nœud parent (nœud parent) : si un nœud contient des nœuds enfants , ce nœud est appelé le nœud parent de ses nœuds enfants ; comme le montre la figure ci-dessus : A contient B, et A est le nœud parent de B ;
• Nœud enfant (nœud enfant) : le nœud racine du sous-arbre contenu dans un nœud est appelé le nœud enfant du nœud ; comme indiqué ci-dessus : B est inclus dans A, et B est le nœud enfant de A ;
• Nœuds frères : les nœuds avec le même nœud parent sont appelés nœuds frères ; comme indiqué dans la figure ci-dessus : B, C, D, F et G ont un nœud parent commun A, qui est un nœud frère, et il en va de même pour P et Q;
• Le degré de l'arbre : Dans un arbre , le degré du plus grand nœud est appelé le degré de l'arbre ; comme le montre la figure ci-dessus : parmi tous les nœuds, le degré du nœud A est 6, donc le degré de l'arbre est 6 ;
• Le niveau des nœuds : à partir de la définition de la racine , la racine est le premier niveau, les nœuds enfants de la racine sont le deuxième niveau, et le nœud A a 4 niveaux ;
• Hauteur ou profondeur de l'arbre : le niveau maximum de nœuds dans l'arbre ; comme indiqué ci-dessus : la hauteur de l'arbre est de 4 ;
• Nœuds cousins : les nœuds dont les parents se trouvent sur la même couche sont les nœuds cousins ​​les uns des autres ; comme le montre la figure ci-dessus : H, I, N et M sont les nœuds cousins ​​les uns des autres ;
• **Ancêtres des nœuds : **De la racine à tous les nœuds sur les branches de ce nœud ; comme indiqué dans la figure ci-dessus : A est l'ancêtre de tous les nœuds ;
• Descendants : tout nœud du sous-arbre enraciné à un nœud est appelé un descendant du nœud. Comme indiqué ci-dessus : tous les nœuds sont des descendants de A ;
• Forêt : Une collection de m (m>0) arbres disjoints est appelée une forêt.

Parmi les concepts ci-dessus, les points clés à comprendre sont : les nœuds feuilles, les nœuds parents, les nœuds enfants, la hauteur et la profondeur de l'arbre et les descendants des nœuds.

implémentation de l'arborescence

Après avoir lu ce qui précède, avez-vous déjà réfléchi à la manière d'implémenter la structure ci-dessus via le code ? Ensuite, réfléchissons à la manière d'implémenter plus efficacement l'arborescence.

Il existe de nombreuses façons de réaliser l'arbre, et la représentation des données est très simple, mais le nombre d'enfants sous un nœud n'est pas clairement spécifié dans l'arbre, donc la priorité absolue de l'arbre devrait être de savoir comment stocker les enfants de chaque nœud .

**Méthode 1 :** Supposons que le degré de l'arbre est N ;

struct TreeNode
{
    
    
    int data; 					// 用来存储数据的成员
    struct TreeNode* subs[N];   // 用来存储孩子结点（N个度）的指针数组 
} 
//这种方式的缺点显而易见，很有可能会出现不少的数组空间未使用导致内存空间的浪费

**Méthode 2 :** Le degré de l'arbre n'est pas précisé.

struct TreeNode
{
    
    
    int data; 		// 用来存储数据的成员
    SeqList s; 		// 在顺序表里存结点的指针
} 
typedef struct TreeNode SLDataType; // 这里是一个顺序表SeqList
// 这种方式的缺点就是，结构过于复杂。因为SeqList这里已经是一个二级指针

**Méthode 3 :** Stockage de tableau structurel (représentation parent)

// 这种方法的主要操作就是，通过下面的结构体TreeNode存储有效信息，最后将其存储到parentArr数组中。
struct TreeNode // 数组存储信息
{
    
    
    int data; 		// 结点数据
    int parent; 	// 父亲结点的下标位置
} 
struct TreeNode parentArr[10]; // 存储结点的数组
// 在这个TreeNode结构体中，data表示当前结点的数据，而parent为这个结点的父节点的下标位置。根节点标记为-1；写入数据后存入结构体数组；
// 具体存储结果可以参考如下举例

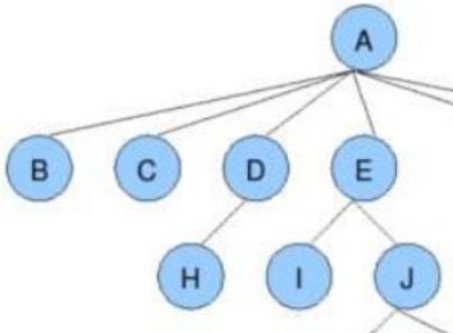
données	UN	B	C	D	E	H	je	J
parent	-1	0	0	0	0	3	4	4
indice	0	1	2	3	4	5	6	7

• données : données de nœud

• parent : la position en indice du nœud parent

• Indice : indice du tableau

​

Les trois méthodes ci-dessus ont leurs propres avantages et inconvénients, mais la méthode la plus courante et la plus pratique est ------ méthode du frère droit de l'enfant gauche
4 : méthode du frère droit de l'enfant gauche. La structure arborescente couramment utilisée est également la structure du frère droit de l'enfant gauche.

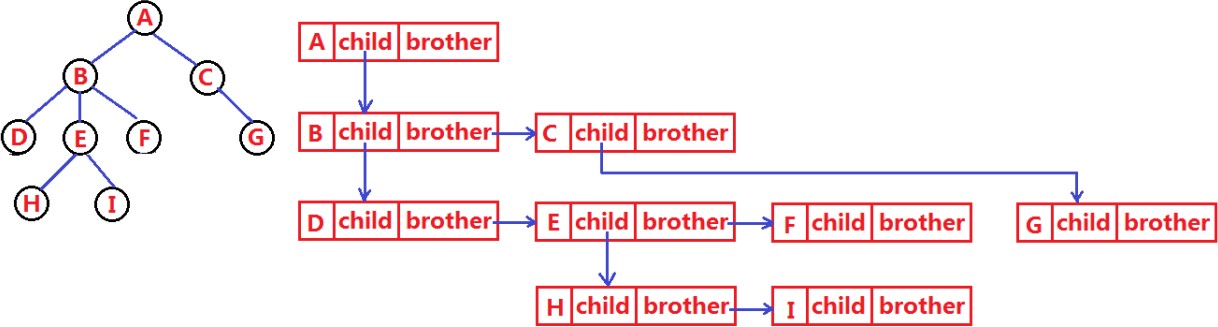
Il commencera d'abord par le nœud racine , enregistrera le premier enfant du nœud enfant à travers l'enfant de gauche à droite , puis utilisera frère pour trouver le nœud frère C, puis utilisera enfant pour enregistrer le nœud enfant afin de continuer la récursivité. De cette manière, quel que soit le nombre de nœuds enfants que possède le nœud parent, il peut être enregistré. Par exemple, si vous souhaitez rechercher les nœuds enfants du nœud A, accédez d'abord au premier enfant via enfant, puis recherchez d'autres nœuds enfants comme si vous parcouriez la liste chaînée.

En même temps, regardons les défauts de cette structure, vous constaterez qu'il n'y a pas de perte de place dans cette structure, et c'est une relation de liaison directe lors de la traversée. Jusqu'à présent, cette structure n'a aucun inconvénient !

Code de référence:

typedef int DataType;
struct Node
{
    
    
    DataType data;				// 节点数据
    struct Node* firstChild;	// 第一个孩子的节点(永远指向第一个孩子，叶子则为NULL)
    struct Node* pNextBrother;	// 指向其下一个兄弟节点(永远指向其的兄弟节点，否则为NULL)
};

données	UN	B	C	D	E	F	g	H	je
premier enfant	B	D	g	NUL	H	NUL	NUL	NUL	NUL
pSuivantFrère	NUL	C	NUL	E	F	NUL	NUL	je	NUL

Concept et structure de l'arbre binaire

Le concept d'arbre binaire :

Un arbre binaire est un ensemble fini de nœuds qui :

1. peut être vide ;

2. Il se compose d'un nœud racine et de deux arbres binaires, également appelés sous-arbre gauche et sous-arbre droit.

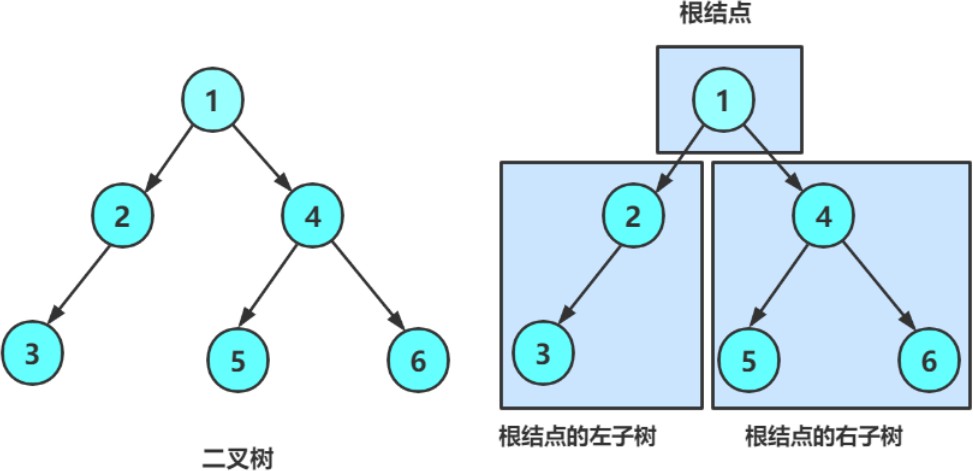
Comme on peut le voir sur la figure ci-dessus :

1. Il n'y a pas de nœud de degré supérieur à 2 dans l'arbre binaire (le degré maximum est 2)

2. Les sous-arbres d'un arbre binaire sont divisés en gauche et droite, et l'ordre ne peut pas être inversé , donc un arbre binaire est un arbre ordonné.

Tout arbre binaire peut avoir les situations suivantes

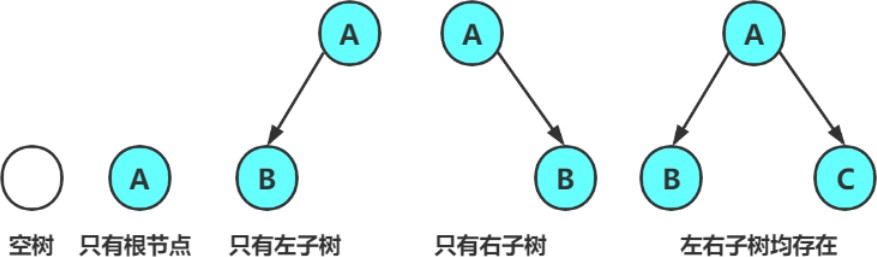
arbre binaire spécial

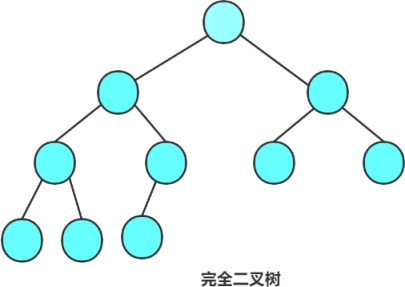
arbre binaire complet

Un arbre binaire est un arbre binaire complet si le nombre de nœuds dans chaque couche atteint la valeur maximale .

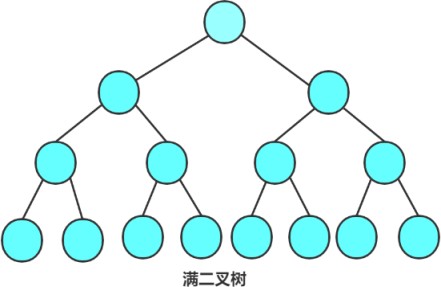
Propriétés d'un arbre binaire complet

• Tous les nœuds feuilles se trouvent dans la dernière couche ;

• Tous les nœuds de branche ont deux enfants ;

• Si le nombre de couches d'un arbre binaire complet est k, alors il y a $2^{k-1}$ nœuds dans la kème couche de l'arbre ;

• Si le nombre de couches d'un arbre binaire complet est h, le nombre total de nœuds dans l'arbre est $2^{h-1}$；

• Si un arbre binaire complet a N nœuds, la hauteur de l'arbre est $log_2 (N+1) $.

arbre binaire complet

Un arbre binaire complet est une structure de données très efficace, et un arbre binaire complet est dérivé d'un arbre binaire complet. Pour un arbre binaire avec une profondeur de K et n nœuds, on l'appelle un arbre binaire complet si et seulement si chaque nœud a une correspondance univoque avec les nœuds numérotés de 1 à n dans l'arbre binaire complet avec une profondeur de K Il convient de noter qu'un arbre binaire complet est un type particulier d'arbre binaire complet .

Propriétés d'un arbre binaire complet :

1. Les premiers étages N-1 sont complets ;

2. La dernière couche n'est pas pleine, mais la dernière couche est continue de gauche à droite. (Par exemple, dans la dernière couche de la figure ci-dessus, si le nœud n'a que des enfants droits mais pas d'enfants gauches, ce n'est pas un arbre binaire complet)

3. Pour un arbre binaire complet de hauteur h, la plage de nœuds est [ $2^{h-1}$ ,$2^h-1$ ]。

Propriétés des arbres binaires

Les propriétés d'un arbre binaire peuvent avoir les points suivants :

1. Si le nombre de couches du nœud racine est spécifié comme 1, alors il y a au plus 2 i − 1 2^{i-1} sur la ième couche d' un arbre binaire non vide$2^{i-1}$ nœuds.

2. Si le nombre de couches du nœud racine est spécifié comme 1, alors le nombre maximum de nœuds dans un arbre binaire avec une profondeur de h est $2^h-1$ .

(Le numéro de chaque couche est une séquence géométrique)

3. Pour tout arbre binaire , si le degré est 0, le nombre de nœuds feuilles est $n_{}$, le nombre de nœuds de branche de degré 2 est $n_{}$, alors il y a $n_{}$= $n_{}$+1 (un degré de 0 vaut toujours un de plus qu'un degré de 2)

4. Si le numéro de couche du nœud racine est spécifié comme 1 , il a ** nnLa profondeur hh$d\text{'}un\; arbre\; binaire\; complet\; de\; n$ nœuds$h$，**$h=lo{g}_{}(n+1)$

5. Pour un arbre binaire complet , si tous les nœuds sont numérotés à partir de 0 selon l'ordre du tableau de haut en bas et de gauche à droite , alors pour le nœud de numéro d'ordre i :

   1. Si i>0, le numéro parent du i nœud de position : (i-1)/2 ;i=0, i est le numéro du nœud racine, pas de nœud parent ;

   2. Si 2i+1<n, numéro de série enfant gauche : 2i+1, 2i+1>=n sinon il n'y a pas d'enfant gauche ;

   3. Si 2i+2<n, le numéro de série du bon fils : 2i+2, 2i+2>=n, sinon il n'y a pas de bon fils .

6. Un arbre binaire complet doit être un arbre binaire complet, mais un arbre binaire complet n'est pas nécessairement un arbre binaire complet.

Structure de stockage arborescente binaire

Les arbres binaires peuvent généralement être stockés en utilisant deux structures, une structure séquentielle et une structure en chaîne.

structure séquentielle

Le stockage à structure séquentielle utilise des tableaux pour le stockage ** Le stockage séquentiel à arbre binaire est physiquement un tableau et logiquement un arbre binaire. **Cependant, en réalité, seul le tas sera stocké dans un tableau, et le tas sera spécifiquement expliqué dans les chapitres suivants.

Le stockage séquentiel d'arbre binaire ne convient généralement que pour représenter un arbre binaire complet , car un arbre binaire complet ne gaspillera pas d'espace.

Comme on peut le voir sur la figure ci-dessus, grâce au stockage séquentiel, on constatera qu'ils sont stockés très régulièrement, et chaque nœud peut être bien représenté. Dans le cas d'un stockage séquentiel, la position en indice de son nœud parent ou de ses enfants gauche et droit peut être calculée via l'indice du nœud.

En supposant que parent est l'indice du nœud parent dans le tableau, alors :

enfant gauche = parent * 2 + 1 enfant droit = ​​parent * 2 + 2

En supposant que l'enfant est un nœud enfant, indépendamment de gauche et de droite, il y a :

parent = (enfant - 1) / 2

// Cela jouera un rôle très important dans l'implémentation du tas plus tard.

chaîne de stockage

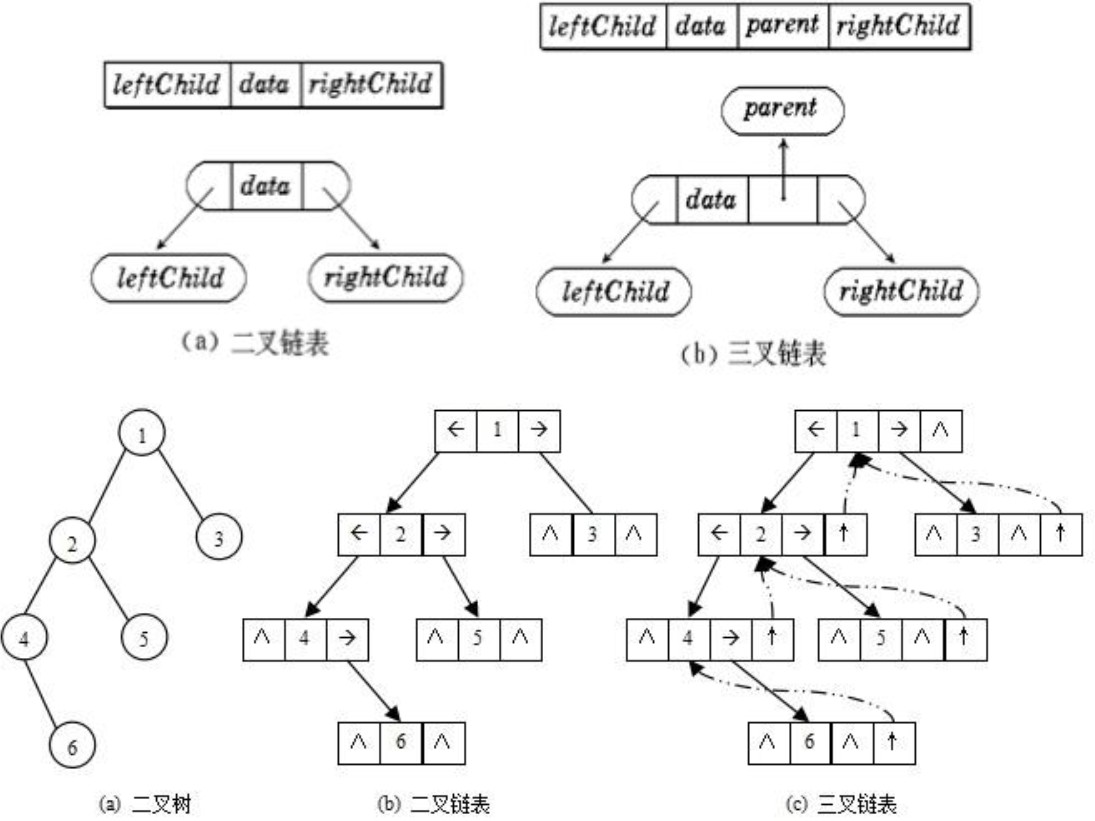
La structure de stockage liée de l'arbre binaire signifie qu'une liste liée est utilisée pour représenter un arbre binaire, c'est-à-dire qu'un lien est utilisé pour indiquer la relation logique des éléments. La méthode habituelle est que chaque nœud de la liste chaînée est composé de trois champs, le champ de données et les champs de pointeur gauche et droit, et les pointeurs gauche et droit sont utilisés pour donner les adresses de stockage des points de lien où l'enfant gauche et l'enfant droit du nœud sont localisés.

La structure de la chaîne est divisée en chaîne à deux fourches et chaîne à trois fourches

Chaîne binaire : il y a deux pointeurs pointant vers les enfants gauche et droit

Chaîne trident : il n'y a pas seulement deux pointeurs pour stocker les enfants gauche et droit, mais également un pointeur pour stocker l'emplacement du nœud parent.

Généralement, les chaînes binaires sont utilisées et les chaînes triples sont utilisées dans les structures de données de haut niveau telles que les arbres rouge-noir.

questions de réflexion

1. Il y a 399 nœuds dans un arbre binaire, parmi lesquels il y a 199 nœuds de degré 2, alors le nombre de nœuds feuilles dans l'arbre binaire est ( )

   A. Il n'y a pas un tel arbre binaire

   B、200

   C、198

   D、199

2. Dans un arbre binaire complet à 2n nœuds, le nombre de nœuds feuilles est ( )

   Un

   B、n+1

   C、n-1

   D、n/2

3. Le nombre de nœuds dans un arbre binaire complet est 531, alors la hauteur de cet arbre est ( )

   A、11

   B、10

   C、8

   J、12

4. Un arbre binaire complet avec 767 nœuds, le nombre de nœuds feuilles est ()

   A、383

   B、384

   C、385

   D、386

Réponse de référence :

1. Réponse : B,

   Analyse : nœud feuille : un nœud de degré 0 est appelé nœud feuille ; et dans la nature d'un arbre binaire, il y a toujours un nœud de degré 0 de plus qu'un nœud de degré 2. Il y a 199 nœuds avec un degré 2 dans la question, puis l'autre Il y a 199+1=200 nœuds feuilles (degré 0) ;

2. Réponse : A,

   Analyse : Cette question utilise la méthode de dérivation des propriétés ;

Soit $X_{}$, le nombre de nœuds de degré 1 est $X_{}$, le nombre de nœuds de degré 0 est $X_{}$, et d'après le titre il a 2n nœuds

∴ L'équation du nombre total de nœuds disponibles est : $X_{}$+ $X_{}$+ $X_{}$= 2n ;

∵ Dans tout arbre binaire, celui de degré 0 est toujours un de plus que celui de degré 2, soit : $X_{}$= $X_{}$- 1;

∴ obtenir l'équation 2 $X_{}$+ $X_{}-1$ = 2n;

Demander le nombre de nœuds feuilles dans la question, c'est-à-dire demander $X_{}$Combien est le nombre, mais maintenant $X_{}$(degré 1) ne peut être obtenu, passons maintenant en revue la nature de l'arbre binaire complet.

Dans un arbre binaire complet, les N-1 premiers niveaux sont pleins et le dernier niveau ne l'est pas, mais le dernier niveau est continu de gauche à droite . Nous pouvons maintenant conclure que la plage du nombre de nœuds avec un degré de 1 dans un arbre binaire complet est $X_{}$∈ [0, 1], il y a au plus un nœud de degré 1.

Revenons à cette question encore une fois, l'équation 2 $X_{}$+ $X_{}$-1 = 2n ;, et la plage de valeurs de x1 est [0, 1], alors $X_{}$

Peut être 0 ou 1. Que $X_{}$Qu'est-ce qui serait bien ?

Quand $X_{}$= 0, l'équation du nœud est 2 $X_{}$- 1 = 2n，$X_{}$= (2n+1) ÷ 2 ;

Quand $X_{}$= 1, l'équation du nœud est 2 $X_{}$= 2n, $X_{}$=n;

∵ $X_{}$= 1, $X_{}$Nombre non entier, ignoré ;

∴ $X_{}$= 1 correspond au sens de la question, donc la réponse est A n;

Cette question doit non seulement combiner les propriétés d'un arbre binaire complet, mais doit également être combinée avec une formule pour résoudre le problème.C'est une très bonne question. Essayez de calculer la quatrième question du même type !

3. Réponse : B,

   Analyse : Dans la nature de l'arbre binaire complet, nous avons mentionné qu'un arbre binaire complet avec une hauteur de h a une plage de nœuds dans [ $2^{h-1}$ ,$2^h-1$ ]. Alors, à quoi devrait ressembler son processus de raisonnement ?

   Dans un arbre binaire complet, la situation la plus importante est que le nombre de nœuds dans la dernière couche de l'arbre binaire complet est plein, ce qui est un arbre binaire complet, donc la valeur maximale peut être prise à 2 h − 1 2^h $2^h-1$ , alors quelle est la valeur minimale ? Imaginez, la situation avec la dernière couche la plus petite devrait être qu'il n'y a qu'un seul nœud dans la dernière couche, qui sont tous le nombre de nœuds dans la couche précédente plus 1, donc lorsque le nombre maximum de couches est h, le nombre de nœuds dans la couche h-1 est$2^{h-1}-1$ , plus les nœuds de la dernière couche est$2^{h-1}-1+1$ , il existe donc un arbre binaire complet de hauteur h dont la plage de numéros de nœuds est [$2^{h-1}$ ,$2^h-1$ ]。

En résumé, lorsque h = 11, la plage du nombre de nœuds de l'arbre binaire complet est [1024, 2047] Lorsque h = 10, la plage du nombre de nœuds de l'arbre binaire complet est [512, 1023] Lorsque h = 8, la plage du nombre de nœuds de l'arbre binaire complet est [128, 255] Lorsque h = 12, la plage du nombre de nœuds de l'arbre binaire complet est [2048, 4095]

Par conséquent, la réponse est B 10

4. Réponse : A 383,

   Analyse : Identique à la question 2.

mots écrits au dos

Les bases de l'arbre binaire sont terminées ! Lors de l'apprentissage des arbres binaires, vous n'apprenez généralement pas directement l'ajout, la suppression, la vérification et la modification des arbres binaires, car les arbres binaires ne sont généralement pas directement utilisés pour stocker des données, mais diverses transformations sont effectuées par des arbres binaires pour répondre à divers besoins, donc dans l'apprentissage Nous accordons plus d'attention à l'apprentissage de la structure et du concept d'arbre binaire dans le cas de l'arbre binaire Plus tard, comme AVL et l'arbre rouge-noir, nous apprendrons à ajouter, supprimer, vérifier et modifier lorsque nous pourrons vraiment stocker des données Lorsque nous commençons à entrer dans l'opération de structure complète de l'arbre binaire, nous devons apprendre un contenu ------ Heap , c'est une structure de données qui doit être comprise avant de commencer à apprendre les arbres binaires.

épilogue

Ce n'est pas facile à créer, si vous pensez que cet article vous est utile, n'oubliez pas de liker et de regarder + suivre !

A l'avenir, nous enverrons les derniers articles sur le compte public WeChat : "01 Programming Cabin" dès que possible. Suivez le cottage et apprenez la programmation sans vous perdre. N'oubliez pas de suivre notre compte public pour ne rien manquer il!