Autor: Yu Fan
fondo
Mirando hacia atrás en la historia del desarrollo de la arquitectura de redes neuronales, podemos encontrar que la simetría siempre ha jugado un papel central y oculto, y el aprendizaje profundo geométrico resalta la importancia de la simetría. Por un lado, en los campos de la visión por computadora tradicional y el procesamiento del lenguaje natural, hemos visto que la arquitectura de red basada en Transformer ha logrado resultados sorprendentes en los últimos años. Por otro lado, como primer principio, la simetría juega un papel importante en las ciencias naturales. Por lo tanto, tenemos razones para creer que desde la perspectiva de la simetría, el aprendizaje profundo geométrico desempeñará un papel importante en la combinación de inteligencia artificial y ciencia.
Figura 1: La combinación del aprendizaje profundo geométrico en los campos de la inteligencia artificial y la ciencia
De hecho, el aprendizaje profundo de la geometría ha logrado resultados impresionantes en el campo de la IA para la ciencia y desempeñará un papel cada vez más importante. Alphafold2, basado en redes neuronales gráficas y Transformer, muestra una precisión muy alta en la predicción de estructuras de proteínas. En la predicción y generación de estructuras de moléculas pequeñas, agregar simetría de transformación de cuerpo rígido adicional (grupo de simetría E (3)) en el espacio euclidiano a la red neuronal del gráfico puede mejorar significativamente la precisión del cálculo y reducir la complejidad del entrenamiento. En la predicción del tiempo global, dado que la superficie de la Tierra es una esfera bidimensional, implica cuestiones como la convolución en la variedad y la transformación de especificación de coordenadas. El aprendizaje profundo geométrico proporciona un marco teórico sistemático para el diseño de redes neuronales. En cosmología, el espacio y el tiempo son curvados debido a la gravedad, y el aprendizaje profundo geométrico proporciona una base teórica para la combinación de esta estructura múltiple curva de Riemann y la IA.
Por otro lado, en campos de las ciencias básicas, como la física de la materia condensada y la física cuántica, el grado de integración con la IA aún no es profundo. Esto se debe a que en estos campos el conocimiento teórico sistemático humano está relativamente bien desarrollado, pero es muy difícil obtener datos de alta calidad. Por lo tanto, es particularmente crítico cómo "inyectar" conocimientos conocidos en las redes neuronales y mejorar la utilización de los datos .
Las redes neuronales grupales equivariantes han mostrado ventajas sorprendentes para mejorar la utilización de datos. Por ejemplo, en la tarea de clasificación del Tetris tridimensional, hay un total de 8 configuraciones. El enfoque tradicional requiere una gran cantidad de rotación espacial de cada configuración de datos para mejorarlos, lo que sin duda aumenta en gran medida la cantidad de datos y la complejidad del entrenamiento, y no puede garantizar la precisión de su predicción. En la red neuronal equivariante E(3), cada configuración solo requiere un dato, o incluso menos si las dos configuraciones se pueden conectar mediante una transformación E(3). Si bien reduce en gran medida la cantidad de datos necesarios , su precisión de predicción está garantizada desde un nivel teórico. Al mismo tiempo, esta red neuronal tiene una mejor interpretabilidad y capacidades expresivas .
Entre todos los conocimientos conocidos, la simetría es un tipo de conocimiento básico y profundo, y también es la clave para explicar las leyes de la naturaleza. Por ejemplo, el espacio-tiempo de las partículas de alta energía tiene simetría del grupo de Lorentz (grupo SO (1, 3)), y las redes neuronales equivariantes del grupo de Lorentz pueden desempeñar un papel importante en la física de alta energía en el futuro. La física moderna se describe utilizando la teoría de campos, y el lenguaje matemático detrás de ella también es la geometría diferencial y los haces de fibras. Es previsible que el aprendizaje profundo de la geometría desempeñe un papel destacado en la combinación de la física moderna y la inteligencia artificial.
Para el modelo grande de IA para la ciencia, basado en el aprendizaje profundo geométrico, podemos tener una idea simple y audaz: primero aprender la simetría del sistema de entrada a través de algún tipo de red neuronal, como aprender el método de álgebra de Lie del grupo de simetría [ 3]; luego, a través de Un cierto mecanismo controla la fuerza de varias simetrías, lo que permite a la red elegir qué grupo de simetría de red equivariante usar, de modo que la red pueda satisfacer la simetría aproximada del sistema de entrada. Por supuesto, existe una alta probabilidad de que los futuros modelos a gran escala no sean tan simples y también están llenos de problemas que aún deben resolverse. Esperamos ver más avances en esta dirección en el futuro.
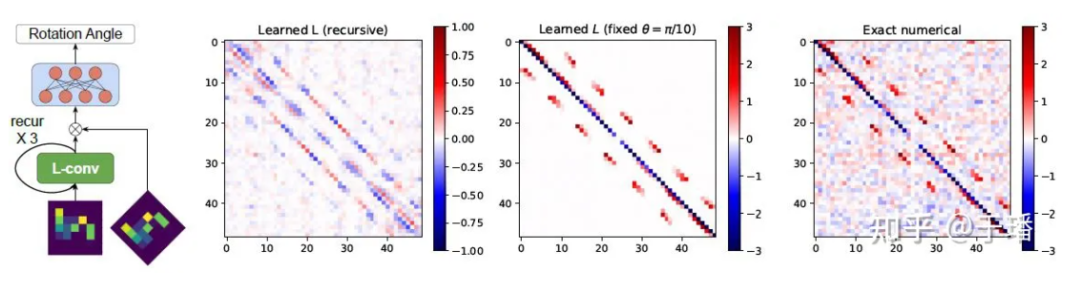
Figura 2: Álgebra de mentira del grupo SO(2) de datos de aprendizaje L-conv
referencias
[1] Bronstein, Michael M., et al. "Aprendizaje profundo geométrico: cuadrículas, grupos, gráficos, geodésicas y medidores". Preimpresión de arXiv arXiv:2104.13478 (2021).
[2] Weiler, Maurice, et al. "Coordinar redes convolucionales independientes: isometría y convoluciones equivalentes de calibre en variedades de Riemann". Preimpresión de arXiv arXiv:2106.06020 (2021).
[3] Dehmamy N, Walters R, Liu Y, et al. Descubrimiento automático de simetría con red convolucional de álgebra de mentiras [J]. Avances en los sistemas de procesamiento de información neuronal, 2021, 34: 2503-2515.
Un programador nacido en los años 90 desarrolló un software de portabilidad de vídeo y ganó más de 7 millones en menos de un año. ¡El final fue muy duro! Google confirmó despidos, relacionados con la "maldición de 35 años" de los codificadores chinos en los equipos Python Flutter Arc Browser para Windows 1.0 en 3 meses oficialmente GA La participación de mercado de Windows 10 alcanza el 70%, Windows 11 GitHub continúa disminuyendo. GitHub lanza la herramienta de desarrollo nativo de IA GitHub Copilot Workspace JAVA. es la única consulta de tipo fuerte que puede manejar OLTP + OLAP. Este es el mejor ORM. Nos encontramos demasiado tarde.
