Cebador
Ahora, dada una matriz arr = [4, 7, 5, 3, 8, 9, 0, 1, 2, 6], arr.length = n, realice las siguientes operaciones de forma repetida e irregular:
- Consulta el valor máximo max dentro del intervalo especificado [l, r] de arr
- Consulta la suma de los elementos en el intervalo especificado [l, r] de arr
- arr agrega C al elemento en la posición del índice i especificado o lo sobrescribe con C
- arr agrega C o anula C para cada valor de elemento en el intervalo especificado [l, r]
en:
- La complejidad temporal de la consulta (intervalo máximo, suma de intervalo) es O(n)
- La complejidad temporal de actualizar un valor único es O (1)
- La complejidad temporal de la actualización de intervalo es O (n)
Si necesita resolver la suma del intervalo especificado de arr varias veces, puede usar el prefijo y la optimización. Para obtener más detalles, consulte:
Sin embargo, en los requisitos anteriores, la matriz arr cambia (actualización de valor único, actualización de intervalo), por lo que el prefijo y la matriz de la matriz arr también cambian. Cada vez que se actualiza arr, el prefijo y la matriz deben regenerarse, por lo que O (1 ) La complejidad del tiempo se calcula como la suma del intervalo.
Si, digamos, realiza cualquiera de las operaciones anteriores m veces (cada operación puede ser diferente), la complejidad temporal final es O(m * n)
Entonces, ¿existe un algoritmo más eficiente?
Concepto de árbol de segmentos
El árbol de segmento de línea es un árbol binario basado en la idea de dividir y conquistar. Cada nodo del árbol de segmento de línea corresponde a un intervalo [l, r] de la matriz arr.
- El nodo hoja del árbol de segmento de línea corresponde a l == r en el intervalo
- Si el nodo no hoja del árbol de segmento de línea corresponde al intervalo [l, r], supongamos mid = (l + r) / 2
- El nodo secundario izquierdo corresponde al intervalo [l, mid]
- El nodo secundario derecho corresponde al intervalo [mid + 1, r]
Los nodos del árbol de segmentos de línea también registran los valores resultantes en el intervalo correspondiente [l, r], como el valor máximo del intervalo y la suma del intervalo.
Es decir, podemos pensar que el nodo del árbol del segmento de línea contiene tres información básica:
- intervalo límite izquierdo l
- el límite derecho del intervalo r
- Valor del resultado del intervalo val
Por ejemplo, la matriz arr = [4, 7, 5, 3, 8, 9, 0, 1, 2, 6], el diagrama de árbol de segmentos correspondiente es el siguiente:
Entre ellos, l == r del nodo hoja en el árbol de segmento de línea, suponiendo i == l == r, entonces el valor del nodo hoja del árbol de segmento de línea es arr [i].
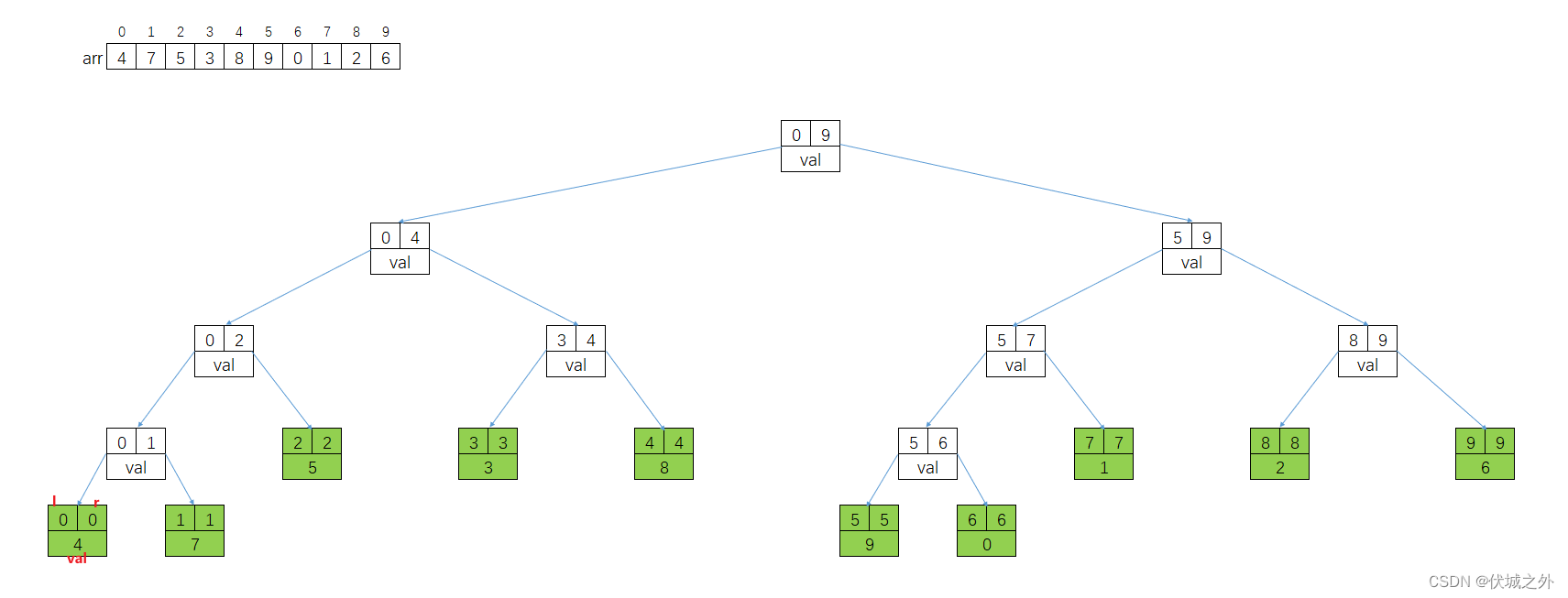
Si necesitamos encontrar el valor máximo del intervalo, el valor de cada nodo padre es equivalente al mayor de los valores de sus dos nodos secundarios, por lo que el árbol de segmentos de línea se puede obtener de la siguiente manera:
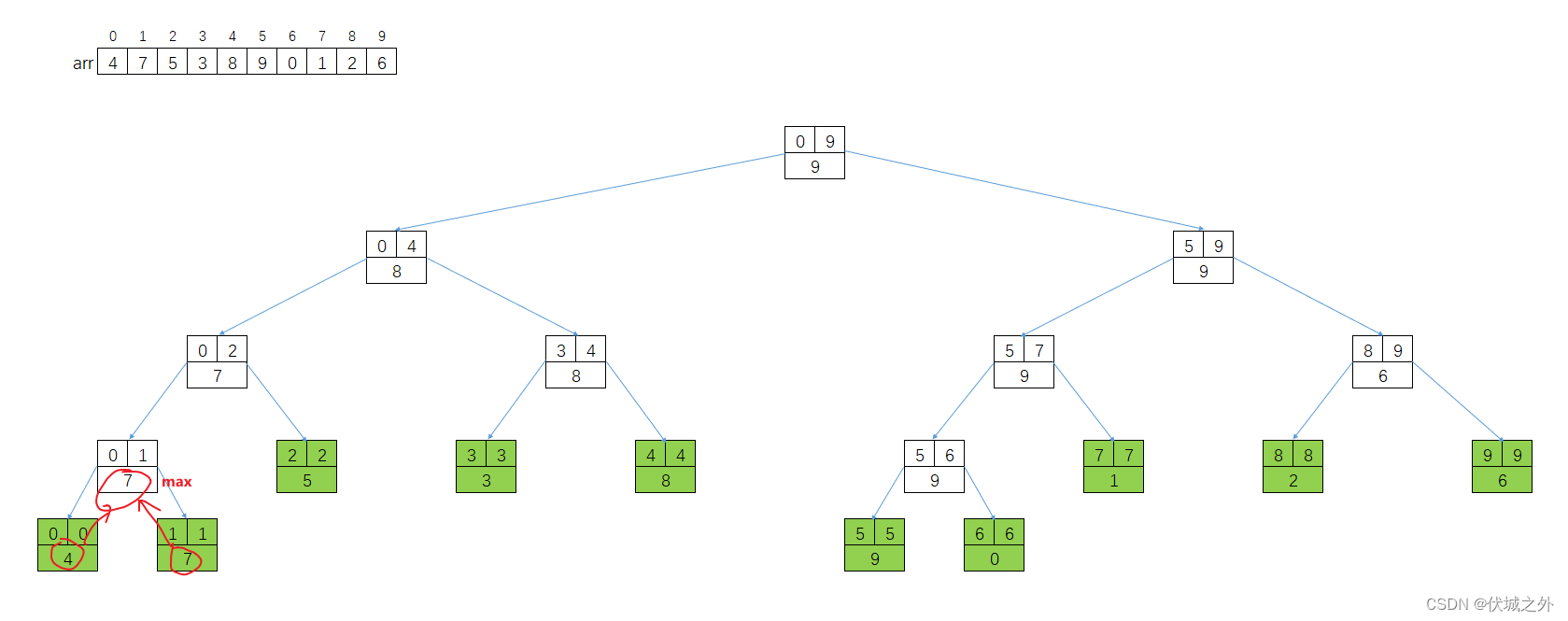
Con la estructura anterior, podemos lograr una complejidad temporal O (logN) y encontrar el valor máximo de cualquier intervalo.
Por ejemplo, si queremos encontrar el valor máximo del intervalo [3, 8], equivale a dividir y conquistar desde el nodo raíz y encontrar los valores resultantes de los tres intervalos [3, 4], [ 5, 7], [8, 8] Tome el valor mayor como el valor máximo del intervalo [3, 8].
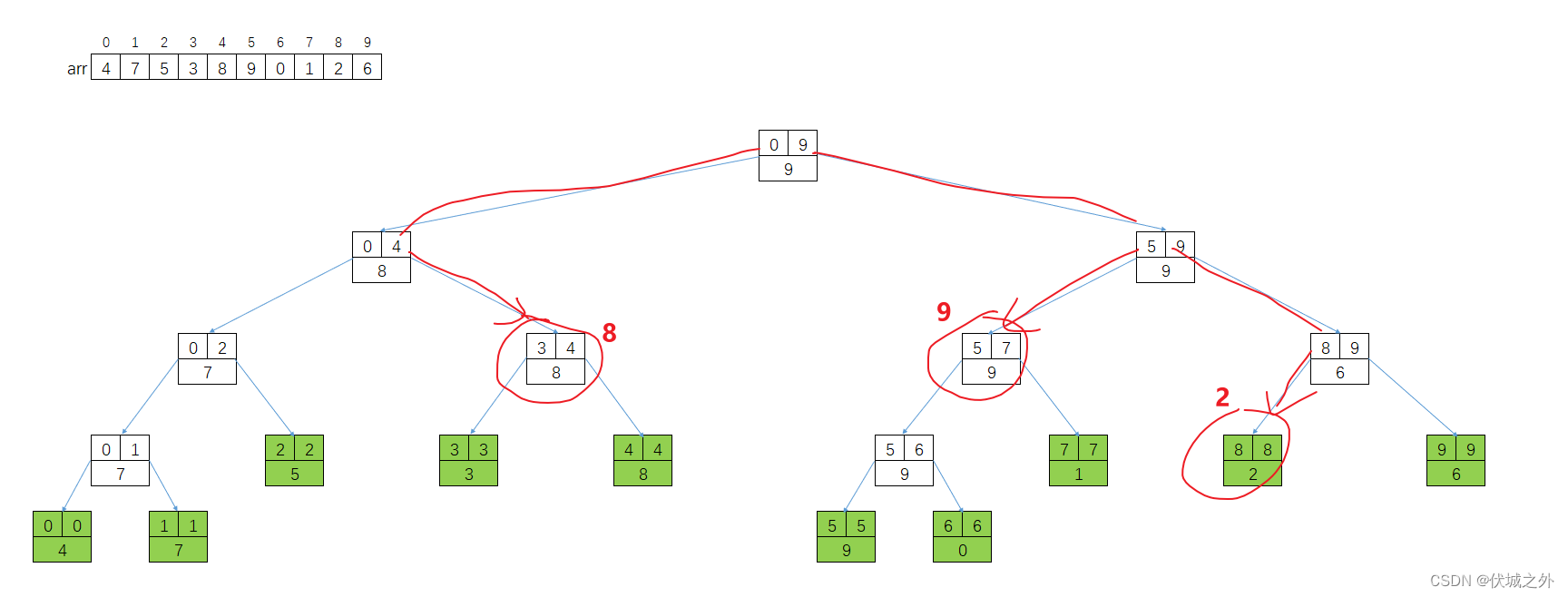
Por lo tanto, es una estrategia muy eficaz consultar información de intervalo basada en el árbol de segmentos de línea.
El contenedor subyacente del árbol de segmentos.
El árbol de segmentos de línea es en realidad un árbol binario y, excepto la última capa que puede no estar llena, el resto de las capas deben estar llenas.
Para un árbol binario completo, podemos almacenarlo en una matriz, como el árbol binario completo que se muestra a continuación:
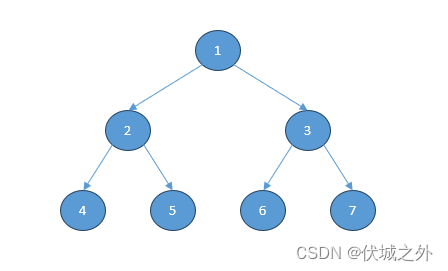
En un árbol binario completo, si el número de serie del nodo padre es k (k>=1), el número de serie de su nodo hijo izquierdo es 2*k y el número de serie de su nodo hijo derecho es 2*k+ 1
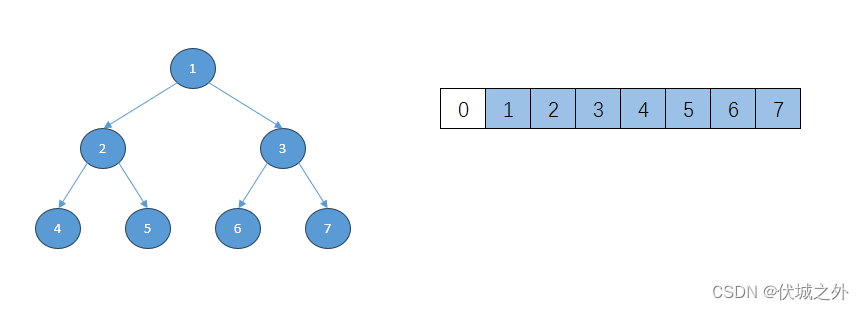
Por lo tanto, si el número completo de nodo del árbol binario corresponde al índice de la matriz, la relación es como se muestra en la figura anterior.
Es decir, el índice k en la matriz registra el valor de nodo del número de nodo k en el árbol binario.
Por lo tanto, siempre que imaginemos el árbol de segmentos de línea como un árbol binario completo, se puede almacenar en una matriz, entonces, ¿cuánto tiempo debe solicitarse el árbol de segmentos de línea?
Suponiendo que el intervalo [l, r] descrito por el árbol de segmentos de línea tiene una longitud de n, significa que el árbol de segmentos de línea tiene n nodos de hoja
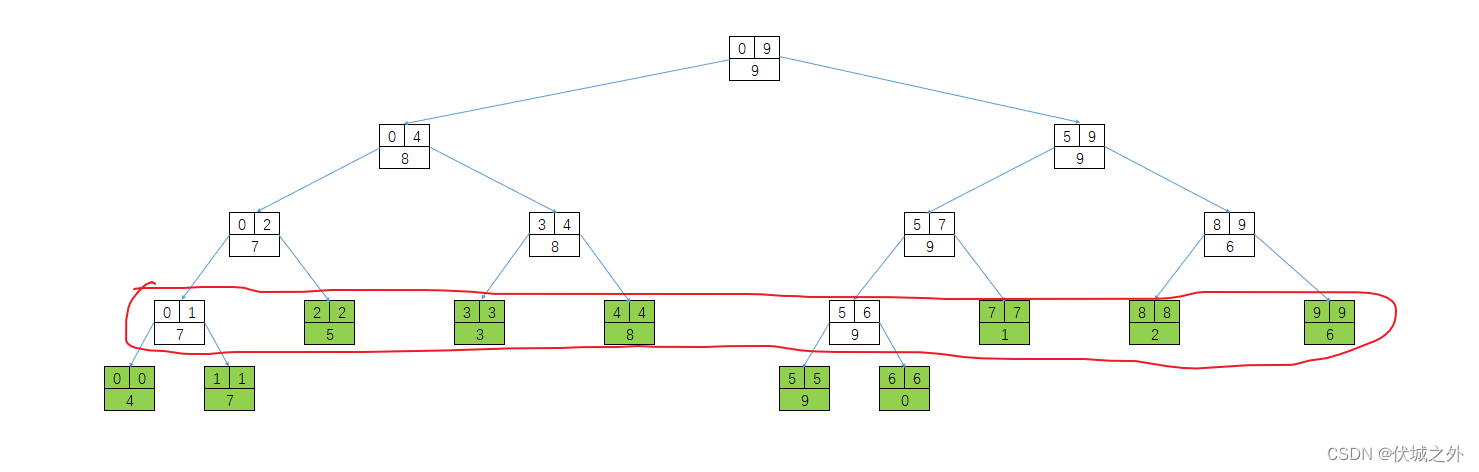
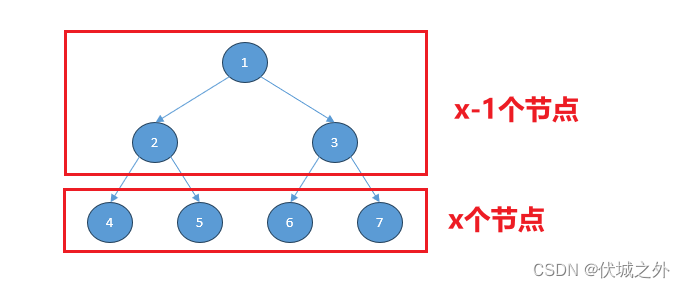
La penúltima capa tiene como máximo n nodos, y la primera a la penúltima capa del árbol de segmento de línea es un árbol binario completo, y el árbol binario completo tiene las siguientes propiedades:
Si hay x nodos en la última capa de un árbol binario completo, la suma del número de nodos en todas las capas anteriores debe ser x-1.
La prueba también es muy sencilla: el número de nodos en cada capa del árbol binario completo:
Capa 1, con 2^0 nodos
Capa 2, con 2^1 nodos
Capa 3, con 2^2 nodos
....
Suponiendo que solo hay 3 capas, debe haber: 2^0 + 2^1 = 2^2 - 1
Si la penúltima capa del árbol de segmentos de línea tiene como máximo n nodos, entonces la penúltima capa del árbol de segmentos de línea tiene como máximo n-1 nodos,
Es decir, hay como máximo 2n-1 nodos desde la primera capa hasta la penúltima capa del árbol de segmentos de línea.
Luego, si se llena la última capa del árbol de segmentos de línea, debe haber como máximo 2n nodos.
Por lo tanto, el árbol de segmentos de línea tiene como máximo 4n nodos en total, es decir, siempre que se abra un espacio de matriz de 4n de longitud, se pueden almacenar todos los nodos del árbol de segmentos de línea.
Construcción de árbol de segmentos de línea
El contenedor subyacente del árbol de segmentos de línea es una matriz, que asumimos que es un árbol.
Si la longitud de la matriz original arr que se va a consultar para obtener información de intervalo es n, entonces la matriz contenedora subyacente del árbol de segmentos de línea debe definir una longitud de 4n.
La relación entre los elementos de la matriz de árbol y los nodos del árbol de segmento de línea es la siguiente:
- elemento de matriz de árbol → nodo de árbol de segmento de línea.
- El índice del elemento de la matriz del árbol → el número de serie del nodo del árbol del segmento de línea
Los nodos del árbol de segmentos de línea contienen tres información básica:
- intervalo límite izquierdo l
- el límite derecho del intervalo r
- Valor del resultado del intervalo val (como suma del intervalo, valor máximo del intervalo)
Por lo tanto, podemos definir una clase de Nodo para registrar información del nodo. Por lo tanto, la matriz de árbol también es una matriz de tipo Nodo.
Podemos usar el diagrama para ver cómo se ve la matriz de árbol.

Construya un árbol de segmentos de línea, es decir, construya una matriz de árbol en la figura anterior.
El índice k de la matriz de árbol es el número de serie k del nodo del árbol del segmento de línea.
árbol[k] = Nodo {l, r, max}
El significado del pseudocódigo anterior es: el nodo del árbol de segmento de línea k corresponde al intervalo de la matriz arr [l, r] y registra el valor máximo máximo en este intervalo
Podemos completar la construcción del árbol de segmentos de línea divide y vencerás de forma recursiva.
Por ejemplo, ya conocemos el nodo del árbol del segmento de línea con k = 1 y el intervalo de arr mantenido es [0, 9] ¿Ahora necesitamos encontrar el valor máximo de este intervalo?
Dado que el segmento de línea es un árbol binario basado en la idea de divide y vencerás, el intervalo [0, 9] se puede dividir en [0, 4] y [5, 9].
Es decir, el problema del valor máximo del intervalo [0, 9] se cambia en dos subproblemas más pequeños del valor máximo del intervalo [0, 4] y el valor máximo del intervalo [5, 9].
El intervalo [0, 4] es exactamente el intervalo mantenido por k=2 nodos, y [5, 9] es el intervalo mantenido por k=3 nodos.
Después de eso, continúe siguiendo esta lógica para resolver recursivamente el valor máximo del intervalo [0, 4] y [5, 9].
Hasta que l == r del intervalo después de dividirse en dos, es decir, cuando se alcanza el nodo hoja, el valor máximo del intervalo [l, r] en este momento es arr [l] o arr [r], y luego puedes empezar a retroceder.
Durante el proceso de retroceso, el valor máximo del intervalo del nodo padre es igual al mayor de los valores máximos de los intervalos de sus dos nodos.
La implementación del código específico es la siguiente (incluido el código de prueba):
Implementación del código JS
// 线段树节点定义
class Node {
constructor(l, r) {
this.l = l; // 区间左边界
this.r = r; // 区间右边界
this.max = undefined; // 区间内最大值
}
}
// 线段树定义
class SegmentTree {
constructor(arr) {
// arr是要执行查询区间最大值的原始数组
this.arr = arr;
// 线段树底层数据结构,其实就是一个数组,我们定义其为tree,如果arr数组长度为n,则tree数组需要4n的长度
this.tree = new Array(arr.length * 4);
// 从根节点开始构建,线段树根节点序号k=1,对应的区间范围是[0, arr.length-1]
this.build(1, 0, arr.length - 1);
}
/**
* 线段树构建
* @param {*} k 线段树节点序号
* @param {*} l 节点对应的区间范围左边界
* @param {*} r 节点对应的区间范围右边界
*/
build(k, l, r) {
// 初始化线段树节点, 即建立节点序号k和区间范围[l, r]的联系
this.tree[k] = new Node(l, r);
// 如果l==r, 则说明k节点是线段树的叶子节点
if (l == r) {
// 而线段树叶子节点的结果值就是arr[l]或arr[r]本身
this.tree[k].max = arr[r];
// 回溯
return;
}
// 如果l!=r, 则说明k节点不是线段树叶子节点,因此其必有左右子节点,左右子节点的分界位置是mid
const mid = (l + r) >> 1; // 等价于Math.floor((l + r) / 2)
// 递归构建k节点的左子节点,序号为2 * k,对应区间范围是[l, mid]
this.build(2 * k, l, mid);
// 递归构建k节点的右子节点,序号为2 * k + 1,对应区间范围是[mid+1, r]
this.build(2 * k + 1, mid + 1, r);
// k节点的结果值,取其左右子节点结果值的较大值
this.tree[k].max = Math.max(this.tree[2 * k].max, this.tree[2 * k + 1].max);
}
}
// 测试
const arr = [4, 7, 5, 3, 8, 9, 0, 1, 2, 6];
const tree = new SegmentTree(arr).tree;
console.log("k\t| tree[k]");
for (let k = 0; k < tree.length; k++) {
if (tree[k]) {
console.log(
`${k}\t| Node{ l: ${tree[k].l}, r: ${tree[k].r}, max: ${tree[k].max}}`
);
} else {
console.log(`${k}\t| null`);
}
}
Implementación de código Java
// 线段树定义
public class SegmentTree {
// 线段树节点定义
static class Node {
int l; // 区间左边界
int r; // 区间右边界
int max; // 区间内最大值
public Node(int l, int r) {
this.l = l;
this.r = r;
}
}
int[] arr;
Node[] tree;
public SegmentTree(int[] arr) {
// arr是要执行查询区间最大值的原始数组
this.arr = arr;
// 线段树底层数据结构,其实就是一个数组,我们定义其为tree,如果arr数组长度为n,则tree数组需要4n的长度
this.tree = new Node[arr.length * 4];
// 从根节点开始构建,线段树根节点序号k=1,对应的区间范围是[0, arr.length-1]
this.build(1, 0, arr.length - 1);
}
/**
* 线段树构建
*
* @param k 线段树节点序号
* @param l 节点对应的区间范围左边界
* @param r 节点对应的区间范围右边界
*/
private void build(int k, int l, int r) {
// 初始化线段树节点, 即建立节点序号k和区间范围[l, r]的联系
this.tree[k] = new Node(l, r);
// 如果l==r, 则说明k节点是线段树的叶子节点
if (l == r) {
// 而线段树叶子节点的结果值就是arr[l]或arr[r]本身
this.tree[k].max = this.arr[r];
// 回溯
return;
}
// 如果l!=r, 则说明k节点不是线段树叶子节点,因此其必有左右子节点,左右子节点的分界位置是mid
int mid = (l + r) >> 1;
// 递归构建k节点的左子节点,序号为2 * k,对应区间范围是[l, mid]
this.build(2 * k, l, mid);
// 递归构建k节点的右子节点,序号为2 * k + 1,对应区间范围是[mid+1, r]
this.build(2 * k + 1, mid + 1, r);
// k节点的结果值,取其左右子节点结果值的较大值
this.tree[k].max = Math.max(this.tree[2 * k].max, this.tree[2 * k + 1].max);
}
// 测试
public static void main(String[] args) {
int[] arr = {4, 7, 5, 3, 8, 9, 0, 1, 2, 6};
Node[] tree = new SegmentTree(arr).tree;
System.out.println("k\t| tree[k]");
for (int k = 0; k < tree.length; k++) {
if (tree[k] == null) {
System.out.println(k + "\t| null");
} else {
System.out.println(
k + "\t| Node{ l: " + tree[k].l + ", r: " + tree[k].r + ", max: " + tree[k].max + "}");
}
}
}
}
Implementación de código Python
# 线段树节点定义
class Node:
def __init__(self):
self.l = None
self.r = None
self.mx = None
# 线段树定义
class SegmentTree:
def __init__(self, lst):
# lst是要执行查询区间最大值的原始数组
self.lst = lst
# 线段树底层数据结构,其实就是一个数组,我们定义其为tree,如果lst数组长度为n,则tree数组需要4n的长度
self.tree = [Node() for _ in range(len(lst) * 4)]
# 从根节点开始构建,线段树根节点序号k=1,对应的区间范围是[0, len(lst) - 1]
self.build(1, 0, len(lst) - 1)
def build(self, k, l, r):
"""
线段树构建
:param k: 线段树节点序号
:param l: 节点对应的区间范围左边界
:param r: 节点对应的区间范围右边界
"""
# 初始化线段树节点, 即建立节点序号k和区间范围[l, r]的联系
self.tree[k].l = l
self.tree[k].r = r
# 如果l==r, 则说明k节点是线段树的叶子节点
if l == r:
# 而线段树叶子节点的结果值就是lst[l]或lst[r]本身
self.tree[k].mx = self.lst[r]
# 回溯
return
# 如果l!=r, 则说明k节点不是线段树叶子节点,因此其必有左右子节点,左右子节点的分界位置是mid
mid = (l + r) >> 1
# 递归构建k节点的左子节点,序号为2 * k,对应区间范围是[l, mid]
self.build(2 * k, l, mid)
# 递归构建k节点的右子节点,序号为2 * k + 1,对应区间范围是[mid+1, r]
self.build(2 * k + 1, mid + 1, r)
# k节点的结果值,取其左右子节点结果值的较大值
self.tree[k].mx = max(self.tree[2 * k].mx, self.tree[2 * k + 1].mx)
# 测试代码
lst = [4, 7, 5, 3, 8, 9, 0, 1, 2, 6]
print("k\t| tree[k]")
for k, node in enumerate(SegmentTree(lst).tree):
if node.mx:
print(f"{k}\t| Node[ l: {node.l}, r: {node.r}, mx: {node.mx} ]")
else:
print(f"{k}\t| null")