Tabla de contenido
1. Derivación de la curva de interpolación spline cúbica por partes
1. Los valores de función de puntos adyacentes son iguales.
2. Las primeras derivadas de puntos adyacentes son iguales.
3. Las derivadas de segundo orden de puntos adyacentes son iguales.
4. Condiciones de límites del punto final
2. Conferencia intensiva de casos y simulación de MATLAB
3. Resultados de la simulación
1. Derivación de la curva de interpolación spline cúbica por partes
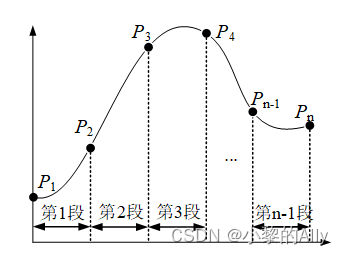
Como se muestra en la Figura 1, hay n puntos discretos y esperamos utilizar una curva suave para pasar por estos n puntos discretos a su vez. Como se mencionó anteriormente, si se utiliza una curva polinómica de alto orden para la interpolación, aparecerá el fenómeno de Runge de oscilación del punto final.
Por lo tanto, prevemos utilizar varias curvas polinómicas de bajo orden para interpolar dos puntos adyacentes y luego conectar sus primeros bits para formar una curva completa suave. Volviendo a la Figura 1, n puntos discretos corresponden a n-1 segmentos de intervalo, es decir, nuestro objetivo es resolver n-1 curvas cúbicas, y la expresión de cada curva cúbica es la siguiente:
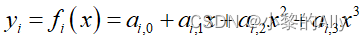
En la fórmula anterior, fi (x) representa la función de curva cúbica del i-ésimo segmento, y ai, j representa el coeficiente del término de orden j de la curva cúbica del i-ésimo segmento.
Se puede ver en la fórmula 1 que cada curva cúbica tiene 4 coeficientes indeterminados, luego n-1 curvas cúbicas tienen un total de 4 (n-1) coeficientes indeterminados, por lo que es necesario construir 4 (n-1) ecuaciones independientes para obtener una solución única. En otras palabras, necesitamos establecer 4 (n-1) condiciones de contorno independientes. El proceso de construcción de condiciones de contorno es en realidad un proceso de exploración de las restricciones de igualdad de curvas cúbicas de múltiples segmentos, que se pueden considerar desde los siguientes aspectos.
1. Los valores de función de puntos adyacentes son iguales.
Obviamente, esperamos que el valor de la función del primer y último punto de cada segmento de la curva cúbica sea igual al punto discreto, la expresión es la siguiente:
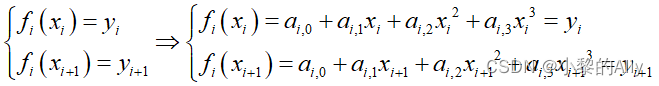
Utilice una expresión matricial en su lugar:
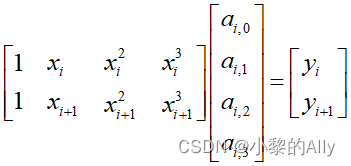
En la fórmula, xi y yi representan la abscisa y la ordenada del punto discreto, respectivamente. Por lo tanto, de acuerdo con la restricción de igualdad de que los valores de la función de los puntos adyacentes son iguales, se pueden construir 2 (n-1) condiciones de contorno.
2. Las primeras derivadas de puntos adyacentes son iguales.
Para garantizar que las derivadas de la curva en puntos adyacentes sean continuas, es necesario asegurarse de que las derivadas de primer orden de los puntos adyacentes sean iguales:
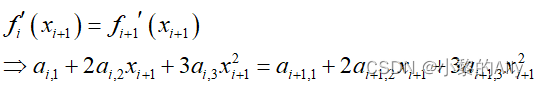
Utilice una expresión matricial en su lugar:
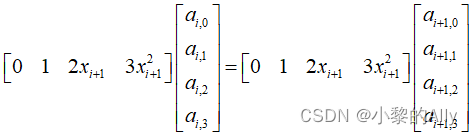
Por lo tanto, las condiciones de contorno (n-2) se pueden construir de acuerdo con la restricción de igualdad de que las derivadas de primer orden de puntos adyacentes son iguales .
3. Las derivadas de segundo orden de puntos adyacentes son iguales.
Para garantizar que la curvatura sea continua, las segundas derivadas de los puntos adyacentes también deben ser iguales:
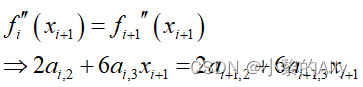
Utilice una expresión matricial en su lugar:
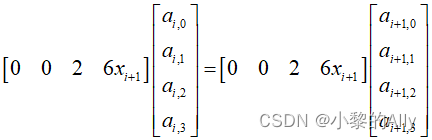
(n-2) las condiciones de contorno se pueden construir de acuerdo con la restricción de igualdad de que las derivadas de segundo orden de puntos adyacentes son iguales .
4. Condiciones de límites del punto final
Las condiciones de límite del punto final se dividen en límite natural, límite fijo y límite torcido. Para el límite natural, la segunda derivada del punto final designado es 0, es decir,
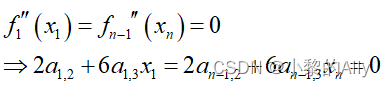
Utilice una expresión matricial en su lugar:
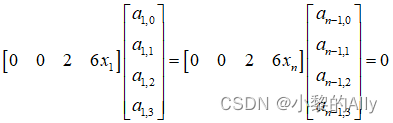
Según la restricción de igualdad de la condición del punto final, se pueden construir dos condiciones de contorno .
En resumen, podemos expresar todas las restricciones de igualdad 4(n-1) anteriores con expresiones matriciales y, finalmente, formar una ecuación matricial lineal, por lo que podemos usar MATLAB para el cálculo matricial y la solución para obtener 4(n-1) coeficiente indeterminado. .
2. Conferencia intensiva de casos y simulación de MATLAB
1. Introducción a la escena
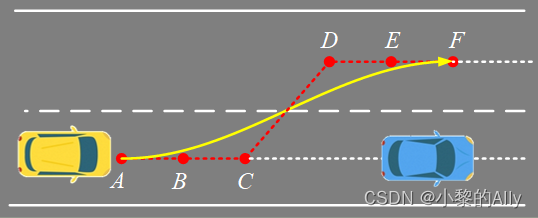
La Figura 2 es un diagrama esquemático de una planificación de ruta local típica: el automóvil azul se utiliza como vehículo de obstáculos y el automóvil amarillo necesita cambiar de carril para evitar obstáculos. Establecemos A(0,-1.75), B(10,-1.75), C(20 ,-1.75) , D(30,1.75 ) , E( 40,1.75 ) , F(50,1.75 ) un total de 6 Los puntos discretos se pueden utilizar para la planificación de rutas utilizando curvas spline cúbicas.
Función de biblioteca de polinomios de interpolación cúbica de Hermite por partes de MATLAB pchip , esta función puede calcular directamente splines cúbicas por partes, devolver 4 coeficientes de cada parte del polinomio y luego llamar a la función de biblioteca ppval de acuerdo con los coeficientes para generar una serie de puntos de interpolación, obteniendo así Cubic splines .
2. programa MATLAB
El programa principal es el siguiente:
% 基于三次样条曲线的换道路径规划
clc
clear
close all
%% 数据定义
d = 3.5;
k = 4;
P = [0,-d/2; 10,-d/2; 20,-d/2; 30,d/2; 40,d/2; 50,d/2]';
%% 调用pchip函数,生成三次样条曲线
x_seq = P(1,:);
y_seq = P(2,:);
cs = pchip(x_seq,y_seq);
X_seq = linspace(0,50,100);
Y_seq = ppval(cs,X_seq);
path = [X_seq', Y_seq'];
%% 计算长度和曲率
x = path(:,1)';
y = path(:,2)';
diffX = diff(path(:,1));
diffY = diff(path(:,2));
cumLength = cumsum(sqrt(diffX.^2 + diffY.^2)); %长度
heading = atan2(diffY, diffX);
for i = 1:length(x)-2
cur(i) = getCur(x(i:i+2)',y(i:i+2)');
end
cur(end+1) = cur(end);
%% 画曲率图
figure
hold on
grid on
% 主体图形绘制
plot(cumLength,cur,'LineWidth', 3, 'Color', 'k');
% 坐标轴
set(gca,'LineWidth',2.5,'FontName', 'Times New Roman')
hXLabel = xlabel('路径长度/m');
hYLabel = ylabel('曲率/m^-^1');
% 修改刻度标签字体和字号
set(gca, 'FontSize', 16),...
set([hXLabel, hYLabel], 'FontName', 'simsun')
set([hXLabel, hYLabel], 'FontSize', 16)
% 画航向角图
figure
hold on
grid on
% 主体图形绘制
plot(cumLength, heading,'LineWidth', 3, 'Color', 'b');
% 坐标轴
set(gca,'LineWidth',2.5,'FontName', 'Times New Roman')
hXLabel = xlabel('路径长度/m');
hYLabel = ylabel('航向角/rad');
% 修改刻度标签字体和字号
set(gca, 'FontSize', 16),...
set([hXLabel, hYLabel], 'FontName', 'simsun')
set([hXLabel, hYLabel], 'FontSize', 16)
%% 画图
d = 3.5; % 道路标准宽度
W = 1.8; % 汽车宽度
L = 4.7; % 车长
figure
len_line = 50;
% 画灰色路面图
GreyZone = [-5,-d-0.5; -5,d+0.5; len_line,d+0.5; len_line,-d-0.5];
fill(GreyZone(:,1),GreyZone(:,2),[0.5 0.5 0.5]);
hold on
fill([P(1,1),P(1,1),P(1,1)-L,P(1,1)-L],[-d/2-W/2,-d/2+W/2,-d/2+W/2,-d/2-W/2],'y')
fill([35,35,35-L,35-L],[-d/2-W/2,-d/2+W/2,-d/2+W/2,-d/2-W/2],'b')
% 画分界线
plot([-5, len_line],[0, 0], 'w--', 'linewidth',2); %分界线
plot([-5,len_line],[d,d],'w','linewidth',2); %左边界线
plot([-5,len_line],[-d,-d],'w','linewidth',2); %左边界线
% 设置坐标轴显示范围
axis equal
set(gca, 'XLim',[-5 len_line]);
set(gca, 'YLim',[-4 4]);
% 绘制路径
scatter(P(1,:),P(2,:),100,'r.')
plot(P(1,:),P(2,:),'r');%路径点
plot(path(:,1),path(:,2), 'y','linewidth',2);%路径点
El programa principal anterior utiliza la función para resolver la curvatura de puntos dispersos, y el programa del cuerpo de la función es el siguiente
function k=getCur(x,y)
ta=sqrt((x(2)-x(1))^2+(y(2)-y(1))^2);
tb=sqrt((x(3)-x(2))^2+(y(3)-y(2))^2);
M=[1,-ta,ta^2;
1,0,0;
1,tb,tb^2];
A=M\x;
B=M\y;
k=(2*(A(2)*B(3)-A(3)*B(2)))/((A(2)^2+B(2)^2)^1.5+1e-10);
end3. Resultados de la simulación
Ejecute el código anterior para dibujar juntos el gráfico de escena y la ruta planificada, como se muestra en la Figura 3.

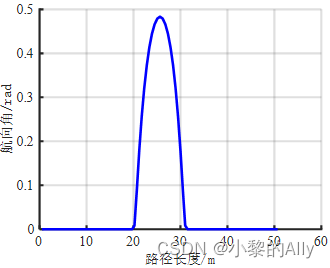
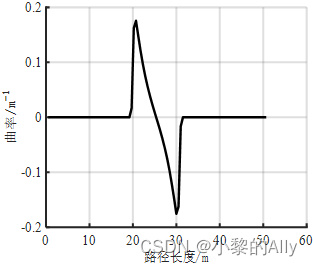
Se puede ver que la tasa de cambio de curvatura de la curva spline cúbica es relativamente grande, lo que tiene una gran relación con la selección de puntos de control.