¿Qué es la transformada de Fourier?
La transformada de Fourier lleva el nombre del matemático francés Jean-Baptiste Joseph Fourier
en honor a sus contribuciones a esta herramienta matemática. Fourier vivió a fines del siglo 18 y principios del siglo 19. Fue un científico polifacético que no solo logró logros sobresalientes en el campo de las matemáticas, sino que también hizo importantes contribuciones en los campos de la conducción del calor y la astrofísica.
La primera forma de la transformada de Fourier fue introducida por primera vez en 1822 por Fourier, quien describió un método para descomponer una función periódica en una serie de funciones de seno y coseno en su libro "Método analítico para resolver la ecuación del calor". Su trabajo sentó las bases para el análisis moderno en el dominio de la frecuencia en el procesamiento de señales, el procesamiento de imágenes y otros campos.
La transformada de Fourier lleva el nombre de Fourier porque fue el primero en estudiar y aplicar sistemáticamente esta herramienta matemática. El trabajo de Fourier ha influido profundamente en la ciencia moderna, especialmente en los campos del procesamiento de señales, el procesamiento de imágenes y la comunicación.La transformada de Fourier se usa ampliamente para analizar y procesar diferentes tipos de señales y datos.
¿Cuál es la transformación en la transformada de Fourier?
En la transformada de Fourier, "transformar" se refiere a convertir una función de una representación en el dominio del tiempo (dominio del tiempo) a una representación en el dominio de la frecuencia (dominio de la frecuencia). En otras palabras, la transformada de Fourier transforma una función de describir su comportamiento en diferentes momentos a describir sus componentes en diferentes frecuencias.
En la transformada de Fourier, transformamos una función (generalmente una señal o imagen). Esta función puede ser continua o discreta. La transformada continua de Fourier (CFT) se aplica a una señal de tiempo continuo, transformándola del dominio del tiempo al dominio de la frecuencia continua. La transformada discreta de Fourier (DFT) se aplica a una señal de tiempo discreto, transformándola del dominio del tiempo al dominio de la frecuencia discreta.
¿Qué se transforma en opencv?
En OpenCV, Fourier Transform (Transformada de Fourier) es una transformación realizada en una imagen, convirtiendo la imagen del dominio espacial (dominio del tiempo) al dominio de la frecuencia. Específicamente,
la transformada de Fourier en OpenCV es la transformada de Fourier discreta (DFT), que se utiliza para convertir una imagen discreta del dominio del tiempo al dominio de la frecuencia discreta.
En la transformada de Fourier, OpenCV 对输入的图像进行数学变换,将图像的每个像素表示为一系列正弦和余弦波的振幅和相位. Esto convierte una imagen de su representación de píxeles sin procesar en una representación compleja que representa los diferentes componentes de frecuencia en la imagen.
Después de leer la información anterior, todavía no sé qué es, así que sé por qué se llama transformada de Fourier.
La transformada de Fourier es muy abstracta. Muchas personas han usado la transformada de Fourier durante muchos años en ingeniería y no han entendido completamente de qué se trata la transformada de Fourier. Para ilustrar mejor la transformada de Fourier, veamos un ejemplo en la vida.
La tabla 14-1 muestra la fórmula de cierta bebida. La fórmula es una tabla en forma de tiempo. La tabla es muy larga y solo una parte de ella se intercepta aquí. Esta tabla registra las operaciones desde la hora "00:00" hasta una hora específica "00:11".
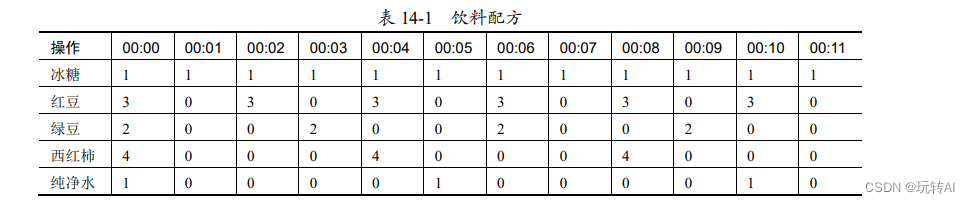
Un análisis cuidadoso de la tabla revela que la fórmula:
- Poner 1 trozo de azúcar de roca cada 1 minuto.
- Ponga 3 frijoles rojos cada 2 minutos.
- Ponga 2 frijoles mung cada 3 minutos.
- Coloque 4 tomates cada 4 minutos.
- Ponga 1 taza de agua purificada cada 5 minutos.
El texto anterior es una explicación de la fórmula desde la perspectiva de la frecuencia de operación.
En el proceso de procesamiento de datos, la información a menudo se expresa en forma de gráficos. Desde la perspectiva del dominio del tiempo, la tabla de recetas se puede expresar como la figura 14-1. La Figura 14-1 solo muestra la operación de la receta en los primeros 11 minutos.Si la operación de la receta se va a expresar completamente, los pasos de la operación en todo el tiempo deben dibujarse con un gráfico.
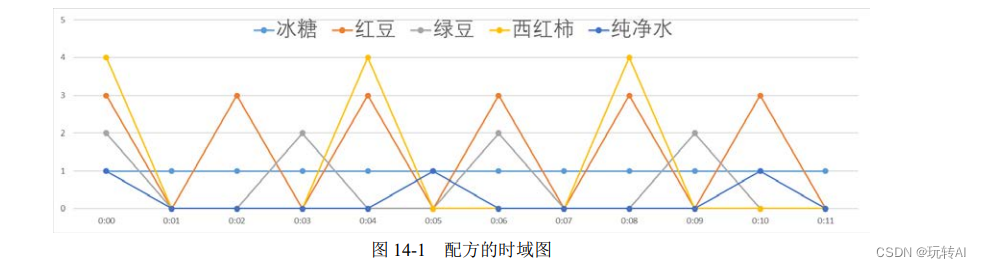
Si se expresa desde la perspectiva de la frecuencia (período), esta tabla de fórmulas se puede expresar como la figura 14-2, donde la abscisa de la figura es el período (recíproco de la frecuencia) y la ordenada es el número de ingredientes.
Se puede ver que la Figura 14-2 puede representar completamente el proceso de operación de esta receta.
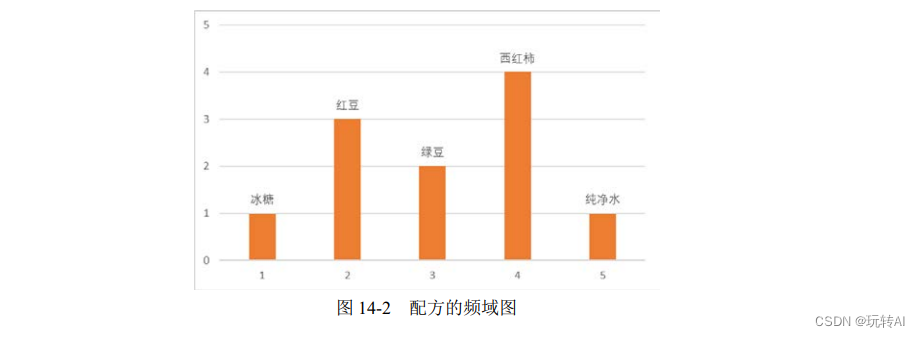
Para funciones, también es posible transformarlo del dominio del tiempo al dominio de la frecuencia .
La figura 14-3 es una sinusoide con frecuencia 5 (5 ciclos en 1 segundo) y amplitud 1.
Si se considera desde la perspectiva de la frecuencia, se puede dibujar como un diagrama de dominio de frecuencia que se muestra en la figura 14-4, donde la abscisa es la frecuencia y la ordenada es la amplitud.
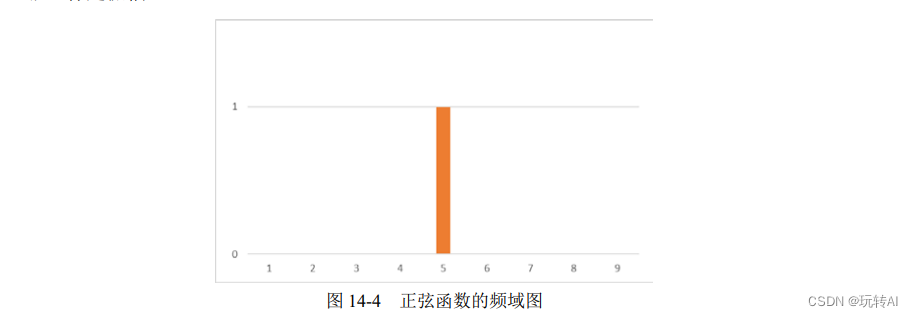
La Figura 14-3 y la Figura 14-4 son equivalentes; son representaciones diferentes de la misma función. La representación en el dominio del tiempo correspondiente se puede obtener a través de la representación en el dominio de la frecuencia, y la representación en el dominio de la frecuencia correspondiente también se puede obtener a través de la representación en el dominio del tiempo.
El matemático francés Fourier señaló que cualquier función periódica puede expresarse como la suma de funciones sinusoidales de diferentes frecuencias. Desde el punto de vista de hoy, esta teoría se da por sentada, pero esta teoría es difícil de entender y fue muy cuestionada en ese momento.
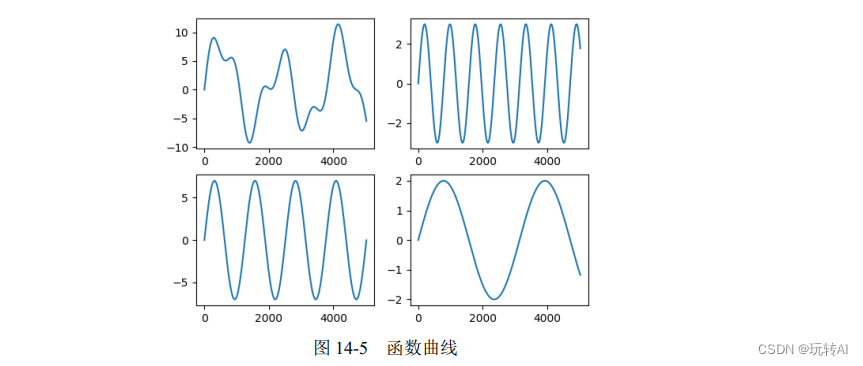
Veamos el proceso específico de la transformada de Fourier. Por ejemplo, la curva de una función periódica se muestra en el gráfico superior izquierdo de la figura 14-5. Esta función periódica se puede expresar como:
y = 3 np.sen(0.8 x) + 7 np.sen(0.5 x) + 2 np.sen(0.2 x)
Por lo tanto, la función puede verse como la suma de las siguientes tres funciones:
- y1 = 3 np.sen(0.8 x) (función 1)
- y2 = 7 np.sen(0.5 x) (función 2)
- y3 = 2 np.sen(0.2 x) (función 3)
Las curvas de función correspondientes a las tres funciones anteriores se muestran en la esquina superior derecha, la esquina inferior izquierda y la esquina inferior derecha de la Figura 14-5, respectivamente.
Si se consideran desde la perspectiva del dominio de la frecuencia, las tres funciones de seno anteriores se pueden expresar como tres columnas en la figura 14-6, donde la abscisa de la figura es la frecuencia y la ordenada es la amplitud.
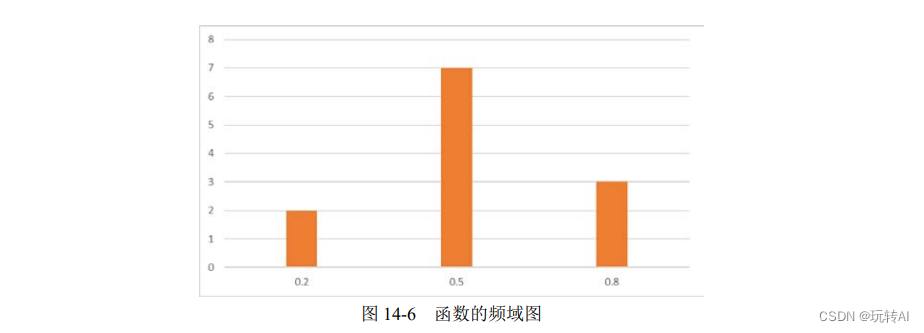
Del análisis anterior, podemos ver que la curva de función en la esquina superior izquierda de la figura 14-5 se puede expresar como el diagrama de dominio de frecuencia que se muestra en la figura 14-6.
El proceso de construir el gráfico de dominio de frecuencia que se muestra en la figura 14-6 a partir del gráfico de función de dominio de tiempo en la esquina superior izquierda de la figura 14-5 es la transformada de Fourier.
La Figura 14-1 y la Figura 14-2 representan la misma información, la Figura 14-1 es un diagrama en el dominio del tiempo y la Figura 14-2 es un diagrama en el dominio de la frecuencia.
El gráfico de función de dominio de tiempo en la esquina superior izquierda de la figura 14-5 es exactamente la misma información que el gráfico de dominio de frecuencia que se muestra en la figura 14-6.
La transformada de Fourier es expresar completamente la información del dominio del tiempo desde la perspectiva del dominio de la frecuencia.
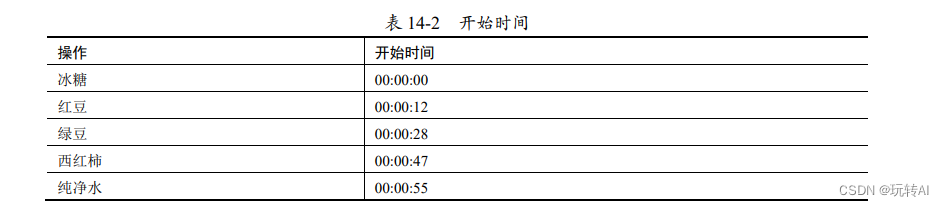
Además de la frecuencia y la amplitud mencionadas anteriormente, también se debe considerar el problema de la diferencia de tiempo. Por ejemplo, las formulaciones de bebidas requieren un control estricto sobre cuándo se agregan los ingredientes para controlar el sabor. La operación a las "00:00" en la Tabla 14-1, bajo un control más fino, se muestra en realidad en la Tabla 14-2.
Si se cambia el momento de agregar los ingredientes, el sabor de la bebida cambiará. Por lo tanto, en el proceso de procesamiento real, también se debe considerar la diferencia de tiempo. Esta diferencia de tiempo es la fase en la transformada de Fourier . La fase representa información relacionada con la diferencia horaria.
Por ejemplo, la función correspondiente a la esquina superior izquierda de la Figura 14-7 se puede expresar como:
y = 3 np.sen(0.8 x) + 7 np.sen(0.5 x+2) + 2 np.sen(0.2 x+3)
Por lo tanto, la función puede verse como la suma de las siguientes tres funciones:
- y1 = 3 np.sen(0.8 x) (función 1)
- y2 = 7 np.sen(0.5 x+2) (función 2)
- y3 = 2 np.sen(0.2 x+3) (función 3)
Las curvas de función correspondientes a las tres funciones anteriores se muestran en la esquina superior derecha, la esquina inferior izquierda y la esquina inferior derecha de la Figura 14-7, respectivamente.
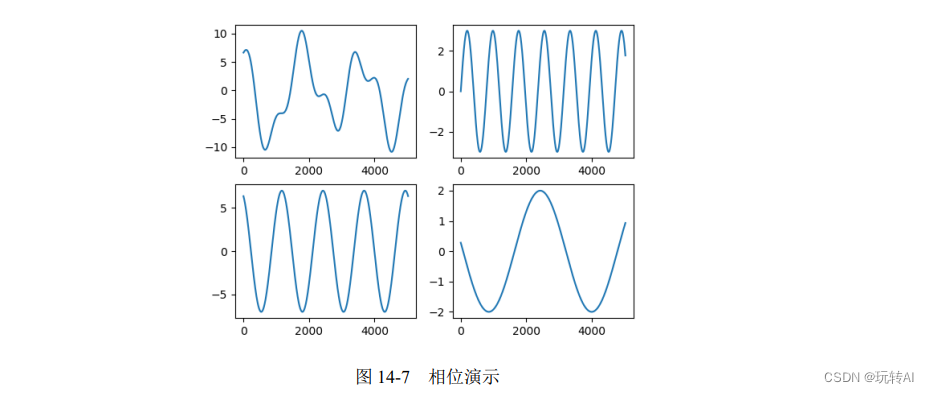
En este ejemplo, si la abscisa se considera como el tiempo de inicio, las tres funciones de seno que constituyen la función y no comienzan todas desde el tiempo 0, y hay una diferencia de tiempo entre ellas. Si se usa directamente la función sin diferencia horaria, no se puede formar la función que se muestra en la esquina superior izquierda de la Figura 14-7, pero se formará la función que se muestra en la esquina superior izquierda de la Figura 14-5.
Por lo tanto, la diferencia de fase también es una condición muy importante en la transformada de Fourier.
Lo anterior utiliza ejemplos de recetas y funciones de bebidas para presentar la viabilidad de la conversión en el dominio del tiempo y el dominio de la frecuencia. Espero que sea útil para que todos entiendan la transformada de Fourier.
En el proceso de procesamiento de imágenes, la transformada de Fourier consiste en descomponer la imagen en dos partes, la componente seno y la componente coseno, es decir, convertir la imagen del dominio espacial al dominio de la frecuencia (en adelante, el dominio de la frecuencia) . Después de que la imagen digital se someta a la transformada de Fourier, el valor del dominio de frecuencia obtenido es un número complejo.
Por lo tanto, para mostrar los resultados de la transformada de Fourier, es necesario utilizar la forma de imagen real más imagen imaginaria (imagen compleja), o imagen de magnitud (imagen de magnitud) más imagen de fase (imagen de fase).
Debido a que la imagen de magnitud contiene la mayor parte de la información que necesitamos en la imagen original, generalmente solo se usa la imagen de magnitud durante el procesamiento de la imagen. Por supuesto, si desea procesar primero la imagen en el dominio de la frecuencia y luego obtener la imagen del dominio espacial modificada a través de la transformada inversa de Fourier, debe conservar la imagen de magnitud y la imagen de fase al mismo tiempo.
Después de realizar la transformada de Fourier en la imagen, obtendremos la información de baja y alta frecuencia en la imagen. La información de baja frecuencia corresponde a componentes de escala de grises que cambian lentamente en la imagen. La información de alta frecuencia corresponde al componente de escala de grises que cambia cada vez más rápido en la imagen, lo que se debe a la transición brusca de la escala de grises.
Por ejemplo, si hay un león en una imagen de una pradera, la información de baja frecuencia corresponde a detalles como la vasta pradera con colores consistentes, mientras que la información de alta frecuencia corresponde a varios bordes e información de ruido, como el contorno de El león.
El propósito de la transformada de Fourier es convertir la imagen del dominio espacial al dominio de la frecuencia y realizar el procesamiento de objetos específicos en la imagen en el dominio de la frecuencia, y luego la transformada inversa de Fourier la imagen del dominio de la frecuencia procesada para obtener la imagen del dominio espacial . La transformada de Fourier juega un papel muy importante en el campo del procesamiento de imágenes, que puede realizar la mejora de la imagen, la eliminación de ruido de la imagen, la detección de bordes, la extracción de características, la compresión y el cifrado de imágenes, etc.
Mirar un montón de descripciones de texto me quema el cerebro, echemos un vistazo al código
Numpy implementa la descripción de la función de transformada de Fourier
El módulo Numpy proporciona la función de transformada de Fourier, y la función fft2() en el módulo Numpy puede realizar la transformada de Fourier de la imagen.
La función proporcionada por Numpy para realizar la transformada de Fourier es numpy.fft.fft2(), y su formato de sintaxis es:
valor de retorno = numpy.fft.fft2 (imagen original)
这里需要注意的是,参数“原始图像”的类型是灰度图像,函数的返回值是一个复数数组(complex ndarray)。
Después del procesamiento de esta función, se puede obtener la información del espectro de la imagen. En este momento, el componente de frecuencia cero en el espectro de la imagen se encuentra en la esquina superior izquierda de la imagen del espectro (imagen de dominio de frecuencia) 1. Para facilitar la observación, la función numpy.fft.fftshift() generalmente se usa para mover el componente de frecuencia cero al centro de la imagen de dominio de frecuencia, como se muestra en la Figura 14-8.
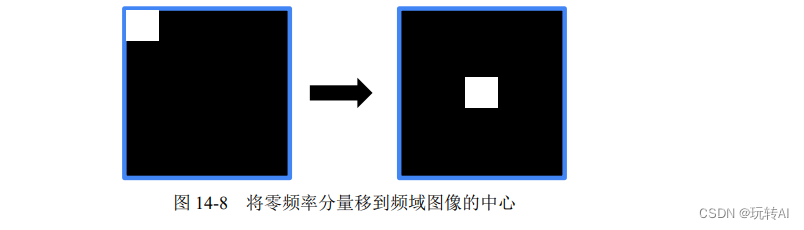
El formato de sintaxis de la función numpy.fft.fftshift() es:
valor devuelto = numpy.fft.fftshift(espectro sin procesar)
Después de procesar con esta función, el componente de frecuencia cero en el espectro de la imagen se moverá al centro de la imagen en el dominio de la frecuencia, lo cual es muy efectivo para observar la parte de frecuencia cero en el espectro después de la transformada de Fourier.
Después de realizar la transformada de Fourier sobre la imagen, lo que se obtiene es una matriz de números complejos. Para que se muestre como una imagen, sus valores deben ajustarse al espacio gris de [0, 255], y la fórmula utilizada es:
Nuevo valor de píxel = 20*np.log(np.abs(valor de espectro))
Ejemplo de código: implemente la transformada de Fourier con Numpy y observe la imagen de espectro obtenida.
el código se muestra a continuación:
import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('lena.png',0)
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
magnitude_spectrum = 20*np.log(np.abs(fshift))
plt.subplot(121)
plt.imshow(img, cmap = 'gray')
plt.title('original')
plt.axis('off')
plt.subplot(122)
plt.imshow(magnitude_spectrum, cmap = 'gray')
plt.title('result')
plt.axis('off')
plt.show()
Resultado de ejecución:
muestra la imagen original y su imagen de espectro

Implementar la transformada inversa de Fourier
Lo que se requiere 注意es que si la función numpy.fft.fftshift() se usa para cambiar el componente de frecuencia cero durante la transformada de Fourier, entonces en el proceso de transformada inversa de Fourier, la función numpy.fft.ifftshift() debe usarse para desplazar primero el componente de frecuencia cero Los componentes de frecuencia se mueven a la posición original y luego se realiza la transformada inversa de Fourier, el proceso se muestra en la Figura 14-10.
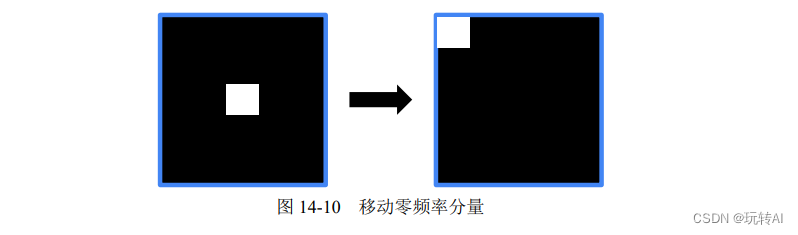
La función numpy.fft.ifftshift() es la función inversa de numpy.fft.fftshift(), y su formato de sintaxis es:
espectro ajustado = numpy.fft.ifftshift(espectro sin procesar)
La función numpy.fft.ifft2() puede implementar la transformada inversa de Fourier y devolver una matriz de números complejos espaciales. Es la función inversa de numpy.fft.fft2(), la sintaxis de esta función es:
Valor de retorno = numpy.fft.ifft2 (datos de dominio de frecuencia)
El valor de retorno de la función numpy.fft.ifft2() sigue siendo un ndarray complejo.
La información del dominio espacial obtenida por la transformada inversa de Fourier es un arreglo complejo, que necesita ser ajustado al espacio de escala de grises [0, 255], la fórmula utilizada es:
iimg = np.abs(resultado de la transformada inversa de Fourier)
Ejemplo: implemente la transformada de Fourier y la transformada inversa de Fourier en Numpy, y observe la imagen resultante de la transformada inversa de Fourier.
import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('lena.png',0)
#对图像进行傅里叶变换,结果是复数
f = np.fft.fft2(img)
#将低频部分移动到图像中心
fshift = np.fft.fftshift(f)
#将复数变化成实数
magnitude_spectrum = 20*np.log(np.abs(fshift))
#将傅里叶变换的结果进行反变换
ishift = np.fft.ifftshift(fshift)
#对傅里叶变换的结果进行反变换
iimg = np.fft.ifft2(ishift)
#取绝对值
iimg = np.abs(iimg)
plt.subplot(131),plt.imshow(img, cmap = 'gray')
plt.title('original'),plt.axis('off')
plt.subplot(132),plt.imshow(magnitude_spectrum, cmap = 'gray')
plt.title('magnitude_spectrum'),plt.axis('off')
plt.subplot(133),plt.imshow(iimg, cmap = 'gray')
plt.title('iimg'),plt.axis('off')
plt.show()
resultado de la operación:

Ejemplo de filtrado de paso alto
En una imagen existen al mismo tiempo señales de alta y baja frecuencia.
- Las señales de baja frecuencia corresponden a componentes de escala de grises que cambian lentamente en la imagen. Por ejemplo, en una imagen de una sabana, la señal de baja frecuencia corresponde a una
amplia extensión de pastizal que tiende a ser de color uniforme. - La señal de alta frecuencia corresponde al componente de escala de grises que cambia cada vez más rápido en la imagen, lo que es causado por la transición brusca de la escala de grises. Si también hay un león en la imagen de la sabana de arriba, entonces la señal de alta frecuencia corresponde a información como el borde del león.
El filtro puede dejar pasar o rechazar un determinado componente de frecuencia, y se puede dividir en un filtro de paso bajo y un filtro de paso alto de acuerdo con su modo de acción.
- Un filtro que permite el paso de señales de baja frecuencia se denomina filtro de paso bajo. Un filtro de paso bajo atenúa las señales de alta frecuencia y pasa las señales de baja frecuencia
会使图像变模糊. - Un filtro que permite el paso de señales de alta frecuencia se denomina filtro de paso alto. Un filtro de paso alto atenúa las señales de baja frecuencia y pasa las señales de alta frecuencia, lo que mejorará los detalles nítidos de la imagen, pero hará que la imagen pierda contraste.
La transformada de Fourier puede separar la señal de alta frecuencia y la señal de baja frecuencia de la imagen

Para establecer todos los valores de píxeles en el medio de la imagen de la derecha en la Figura 14-12 a cero, primero es necesario calcular las coordenadas de su posición central y luego seleccionar un área de 30 píxeles de tamaño de la de arriba a abajo, de izquierda a derecha, con las coordenadas en el centro, y establezca los píxeles de esta área en cero. El valor se establece en cero.
La implementación de este filtro es:
rows, cols = img.shape
crow,ccol = int(rows/2) , int(cols/2)
fshift[crow-30:crow+30, ccol-30:ccol+30] = 0
Ejemplo: Fourier transforma una imagen en Numpy para obtener su imagen en el dominio de la frecuencia. Luego, el valor del componente de baja frecuencia se procesa como 0 en el dominio de la frecuencia para realizar el filtrado de paso alto. Finalmente, se realiza la transformada inversa de Fourier sobre la imagen para obtener la imagen original restaurada.
Observe la diferencia en la imagen antes y después de la transformada de Fourier.
import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('lena.png',0)
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
rows, cols = img.shape
crow,ccol = int(rows/2) , int(cols/2)
fshift[crow-30:crow+30, ccol-30:ccol+30] = 0
ishift = np.fft.ifftshift(fshift)
iimg = np.fft.ifft2(ishift)
iimg = np.abs(iimg)
plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('original'),plt.axis('off')
plt.subplot(122),plt.imshow(iimg, cmap = 'gray')
plt.title('iimg'),plt.axis('off')
plt.show()
resultado de la operación:

OpenCV implementa la transformada de Fourier
OpenCV 提供了函数 cv2.dft()和 cv2.idft()来实现傅里叶变换和逆傅里叶变换, que se presentará por separado a continuación.
Implementar la transformada de Fourier
El formato de sintaxis de la función cv2.dft() es:
Resultado devuelto = cv2.dft (imagen original, logotipo convertido)
Al usar esta función, debe prestar atención a las especificaciones de uso de los parámetros:
- Para el parámetro "imagen original", primero use la función np.float32() para convertir la imagen al formato np.float32.
- El valor de "bandera de conversión" suele ser "cv2.DFT_COMPLEX_OUTPUT", que se utiliza para generar una matriz compleja.
El resultado devuelto por la función cv2.dft() es consistente con el resultado obtenido al usar Numpy para la transformada de Fourier, pero el valor que devuelve es de doble canal, el primer canal es la parte real del resultado y el segundo canal es el
resultado La parte imaginaria de .
Tras la transformación de la función cv2.dft(), obtenemos la información espectral de la imagen original.
En este momento, el componente de frecuencia cero no está en el centro. Para facilitar el procesamiento, debe moverse al centro, lo que puede realizarse mediante la función numpy.fft.fftshift().
Por ejemplo, la siguiente declaración desplaza el componente de frecuencia cero en la imagen del espectro dft al centro del espectro y obtiene el desplazamiento de la imagen del espectro con el componente de frecuencia cero en el centro.
dftShift = np.fft.fftshift(dft)
Después del procesamiento anterior, la imagen espectral es solo un valor compuesto por una parte real y una parte imaginaria. Para mostrarlo, se requiere un procesamiento adicional.
函数 cv2.magnitude()可以计算频谱信息的幅度. La sintaxis de esta función es:
Valor de retorno = cv2.magnitud (parámetro 1, parámetro 2)
Los significados de los dos parámetros en la fórmula son los siguientes:
- Parámetro 1: El valor de la coordenada x del tipo de coma flotante, es decir, la parte real.
- Parámetro 2: El valor de la coordenada y de coma flotante, es decir, la parte imaginaria, que debe tener el mismo tamaño que el parámetro 1 (el tamaño del valor, no el tamaño del valor).
El valor de retorno de la función cv2.magnitude() es la raíz cuadrada de la suma de los cuadrados del parámetro 1 y el parámetro 2, la fórmula es:
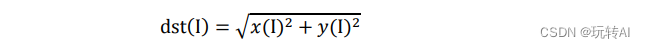
En la fórmula, I representa la imagen original y dst representa la imagen de destino.
Después de obtener la magnitud de la información del espectro, normalmente es necesario convertir adicionalmente el valor de la magnitud para visualizar la información del espectro en forma de imagen. En pocas palabras, es necesario asignar el valor de amplitud al espacio de escala de grises [0, 255] de la imagen en escala de grises, para que se pueda mostrar en forma de imagen en escala de grises.
La fórmula utilizada aquí es:
resultado = 20*np.log(cv2.magnitud(parte real, parte imaginaria))
La siguiente es una transformada de Fourier de una imagen para ayudar a los lectores a observar el procesamiento anterior. El siguiente código realiza la transformada de Fourier en la imagen "lena", calcula el valor de magnitud y normaliza el valor de magnitud:
import numpy as np
import cv2
img = cv2.imread('lena.png',0)
dft = cv2.dft(np.float32(img),flags = cv2.DFT_COMPLEX_OUTPUT)
print(dft)
dftShift = np.fft.fftshift(dft)
print(dftShift)
result = 20*np.log(cv2.magnitude(dftShift[:,:,0],dftShift[:,:,1]))
print(result)
Los rangos de valores obtenidos se muestran en la Fig. 14-14 respectivamente. en:
- La figura de la izquierda muestra el valor espectral obtenido por la función cv2.dft(), que se compone de partes reales e imaginarias.
- La figura del medio muestra los valores de magnitud espectral calculados por la función cv2.magnitude(), que no están en el espacio de escala de grises de la imagen estándar [0, 255].
- La figura de la derecha muestra el resultado de una mayor normalización del valor de la magnitud espectral calculado por la función cv2.magnitude(), y el rango de valores ahora está en [0, 255].

Ejemplo: use la función OpenCV para realizar la transformada de Fourier en una imagen y mostrar su información espectral
import numpy as np
import cv2
import matplotlib.pyplot as plt
img = cv2.imread('lena.png',0)
dft = cv2.dft(np.float32(img),flags = cv2.DFT_COMPLEX_OUTPUT)
dftShift = np.fft.fftshift(dft)
result = 20*np.log(cv2.magnitude(dftShift[:,:,0],dftShift[:,:,1]))
plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('original'),plt.axis('off')
plt.subplot(122),plt.imshow(result, cmap = 'gray')
plt.title('result'), plt.axis('off')
plt.show()
resultado de la operación:
- La imagen de la izquierda es la imagen original.
- La imagen de la derecha es una imagen de espectro, que es el resultado de usar la función np.fft.fftshift() para desplazar el componente de frecuencia cero al centro de la imagen de espectro.

Implementar la transformada inversa de Fourier
En OpenCV, use 函数 cv2.idft()实现逆傅里叶变换, esta función es
la función inversa de la función de transformada de Fourier cv2.dft(). Su formato de sintaxis es:
Resultado de retorno = cv2.idft (datos originales)
Después de la transformación de Fourier de una imagen, el componente de frecuencia cero generalmente se desplaza hacia el centro de la imagen espectral. Si el componente de frecuencia cero se cambia usando la función numpy.fft.fftshift(), entonces se debe usar la función numpy.fft.ifftshift() para restaurar el componente de frecuencia cero a su posición original
antes de realizar la transformada inversa de Fourier .
También tenga en cuenta que después de la transformada inversa de Fourier, el valor resultante sigue siendo un número complejo, y
su magnitud debe calcularse mediante la función cv2.magnitude().
Ejemplo: use la función OpenCV para realizar la transformada de Fourier y la transformada inversa de Fourier en la imagen, y muestre la imagen original y la imagen obtenida después de la transformada inversa de Fourier.
import numpy as np
import cv2
import matplotlib.pyplot as plt
img = cv2.imread('lena.png',0)
#对图像进行傅里叶变换
dft = cv2.dft(np.float32(img),flags = cv2.DFT_COMPLEX_OUTPUT)
#将低频部分移动到图像中心
dftShift = np.fft.fftshift(dft)
#将复数变化成实数
ishift = np.fft.ifftshift(dftShift)
#将傅里叶变换的结果进行反变换
iImg = cv2.idft(ishift)
#取绝对值,取对数的目的为了将数据变化到较小的范围(比如0-255),并显示,结果是复数
iImg= cv2.magnitude(iImg[:,:,0],iImg[:,:,1])
print(iImg.shape)
plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('original'), plt.axis('off')
plt.subplot(122),plt.imshow(iImg, cmap = 'gray')
plt.title('inverse'), plt.axis('off')
plt.show()
resultado de la operación:

La imagen de la derecha es la imagen obtenida después de realizar la transformada de Fourier y la transformada inversa de Fourier en la imagen original img.