Descenso de gradiente del algoritmo de optimización｜Matlab realiza el algoritmo de descenso de gradiente

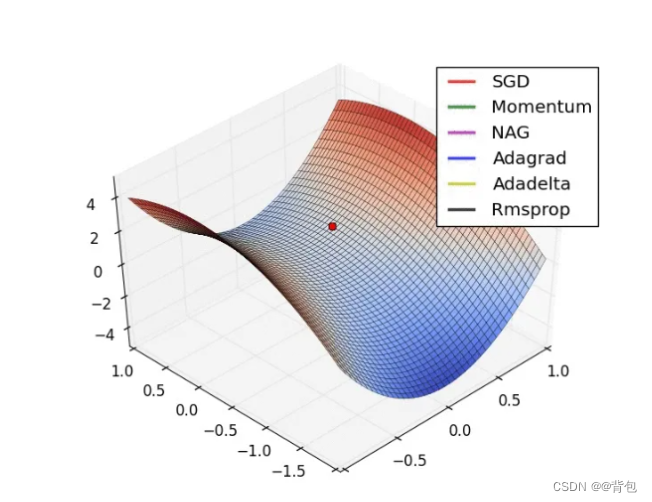
Requisitos del tema:

Método de descenso de gradiente usando Matab

Para una función:
$min f(x)=2 x_{1}^{2}+4 x_{ 2 }^{2}-6 x_{1}-2 x_{1} x_{2}$
Intente usar MATLAB para realizar el método de descenso más pronunciado para resolver este problema y proporcione el proceso iterativo específico, el resultado final de la optimización, el código involucrado y su propia experiencia.

Resumen

El artículo realiza principalmente cálculos de gradiente mediante la implementación grad()de funciones.

Principales funciones realizadas:

Algoritmo de descenso de gradiente realizado por Matlab Language

Use Matlab plot3para representar el proceso de iteraciones del ciclo de descenso de gradiente y también represente la imagen del valor mínimo con el número de iteraciones.

Principio de descenso de gradiente

El concepto de gradiente

Gradiente : Es un vector, que indica que la derivada direccional de una determinada función en este punto obtiene el valor máximo a lo largo de esta dirección.

Hay un tamaño: la tasa de cambio es la mayor (el módulo del gradiente);
Dirigida: la función cambia más rápidamente a lo largo de esa dirección (la dirección de este gradiente) en ese punto

Definición:
Sea $z = f (x, y)$ en $P_{0}\left(x_{0}, y_{0}\right)$ hay una derivada parcial $f_{x}^{\prime}\left(x_{0}, y_{0}\right)$ 和 $f_{y}^{\prime}\left(x_{0}, y_{0}\right)$ ,则称向量 $\left\{f_{x}^{\prime}\left(x_{0}, y_{0 }\derecha), f_{y}^{\principal}\izquierda(x_{0}, y_{0}\derecha)\derecha\}$ para $\text { en} P_{0}\left(x_{0}, y_{0}\right)$ gradiente, indicado como:

$\left.\nabla f\right|_{P_{0}},\left.\nabla z\right|_ {P_{0}},\left.\operatorname{gradf}\right|_{P_{0}} while \left.\operatorname{gradz}\right|_{P_{0}}$
$\left.\therefore \nabla f\right|_{P_{0 }}=\left.\operatorname{gradf}\right|_{P_{0}}=\left\{f_{x}^{\prime}\left(x_{0}, y_{0}\right) , f_{y}^{\principal}\izquierda(x_{0}, y_{0}\derecha)\derecha\}$
donde: $\nabla$ (Nabla)算子:
$\nabla=\frac{\parcial}{\parcial x} i+\frac{\parcial}{\parcial y} j$

Función de gradiente:

Tamaño de degradado:

$|\nabla f|=\sqrt{\left[f_{x}^{\prime}(x, y)\derecha]^{2}+\izquierda[f_{y}^{\principal}(x, y)\derecha]^{2}}$

La dirección del gradiente:

设： $v=\left\{v_{1}, v_{2}\right\}(|v|=1)$ es cualquier dirección dada, entonces para $\nabla f$ y $\theta$ de $v$ $θ$ tiene:

$\begin{alineado} \left.\frac{\partial f}{ \parcial v}\right|_{P_{0}} &=f_{x}^{\prime}\left(x_{0}, y_{0}\right) v_{1}+f_{y}^ {\prime}\left(x_{0}, y_{0}\right) v_{2} \\ &=\left\{f_{x}^{\prime}\left(x_{0}, y_{ 0}\right), f_{y}^{\prime}\left(x_{0}, y_{0}\right)\right\} \bullet\left\{v_{1}, v_{2}\ derecha\} \\ &=\izquierda.\nabla f\derecha|_{P_{0}} \bullet v=|\nabla f|_{P_{0}}|\cdot| v \mid \cos \theta \end{alineado}$

Método de descenso de gradiente:

$\alpha_{(k)}=\operatorname{argmin} f\left(x^{k}-\alpha \cdot \ nabla f\left(x^{(k)}\right)\right)$

Análisis de las ventajas y desventajas del método de descenso de gradiente

ventaja:

(1) El programa es simple y la cantidad de cálculo es pequeña;
(2) No hay un requisito especial para el punto inicial;
(3) El método de descenso más pronunciado es globalmente convergente y linealmente convergente

defecto:

(1) Solo tiene el atributo "más rápido" en el rango local, y su velocidad descendente es lenta para el proceso de solución general; (2) La velocidad se ralentiza
cuando está cerca del valor mínimo;
(3) Puede ser caída en 'zigzag'

Código central y resultados

El resultado de la iteración del código:

Proceso iterativo:
inserte la descripción de la imagen aquí
valor mínimo - número de iteraciones Imagen de tendencia:

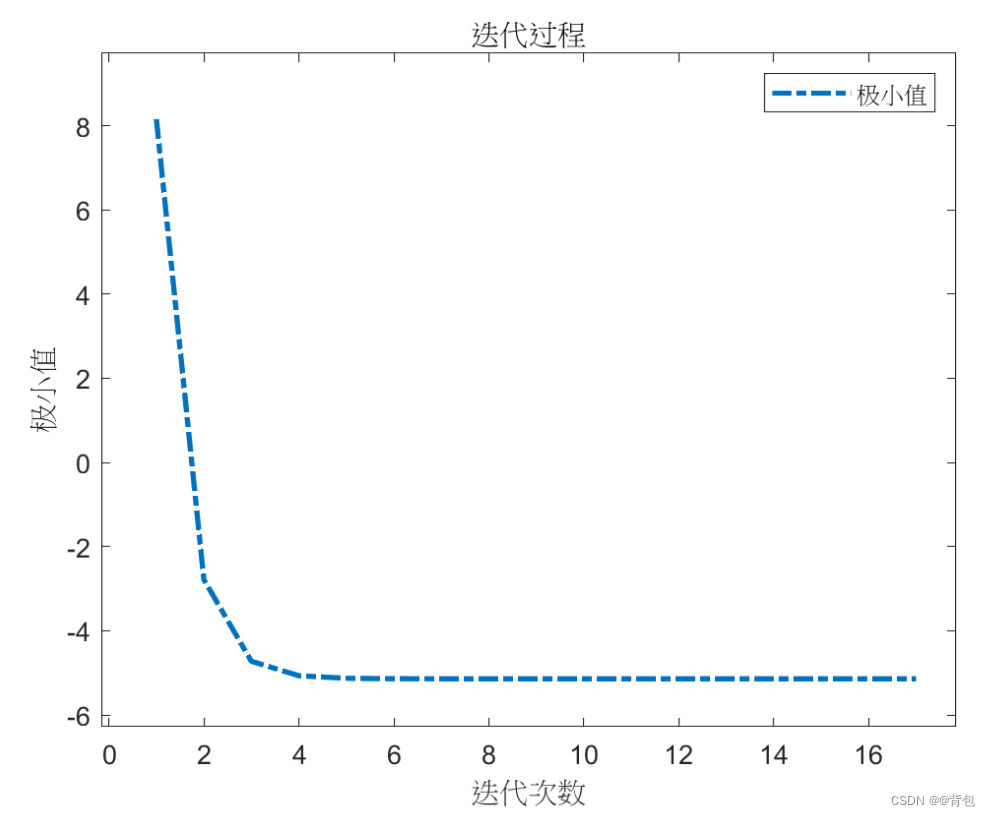
visualización del resultado iterativo en la superficie cónica:

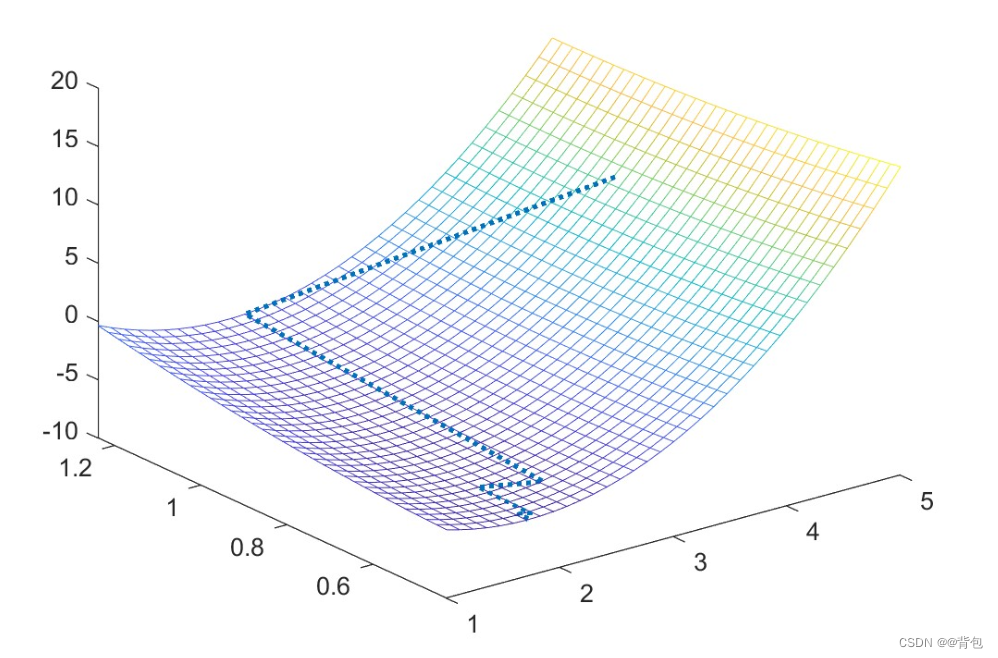
función buscada:
$min f(x)=2 x_{1}^{2}+4 x_{2}^{2}-6 x_{1}-2 x_{1} x_{2}$
función principal:

clc,clear;
syms x1 x2 s; %声明符号变量
f1 =2*x1^2+4*x2^2-6*x1-2*x1*x2;%设定目标函数
[k,f1,f2,f3]=grad(f1,x1,x2,s,[0,1],10^(-5));  %设定起始点[x1 x2]=[-2.5,4.25]和精度10^(-2)
[result]=sprintf('在 %d 次迭代后求出极小值\n',k);%在迭代多少次之后求出极小值
disp(result);
figure(1);
plot(1:k,f3); % 作出函数图像
title('迭代过程');%输出结果
xlabel('迭代次数');
ylabel('极小值'); 
figure(2);
plot3(f1,f2,f3); % 画出方程图像
hold on;
syms x1 x2; % 声明符号变量
f=2*x1^2+4*x2^2-6*x1-2*x1*x2;
fmesh(f);

Implementación de la función principal de descenso de gradiente:

function  [iterator,f1,f2,f3] = grad(f,x1,x2,s,start_point,thereshold) 
    iterator = 0;%迭代次数赋值初始化
    grad_f = [diff(f,x1) diff(f,x2)]; %计算f的梯度 
    delta = subs(grad_f,[x1,x2],[start_point(1),start_point(2)]);
    %计算起点的梯度   
    step=1; %设置初始步长为1
    current_point = start_point;%起点值赋给当前点
    %最速下降法的主循环，判断条件为：梯度的模与所给精度值进行比较
    while norm(delta) > thereshold          
        iterator = iterator + 1;%迭代次数+1     
        %一维探索 求最优步长（此时方向已知，步长s为变量）
        x_next = [current_point(1),current_point(2)] - s* delta/norm(delta);% 计算x（k+1）点，其中步长s为变量 
        f_val = subs(f,[x1,x2],[x_next(1),x_next(2)]);% 将x值带入目标函数中
        step = abs(double(solve(diff(f_val,s)))); % 对s求一阶导，并加绝对值符号，得到最优步长的绝对值
        step = step(1);%更新步长    
        %计算x（k+1）点
        current_point = double([current_point(1),current_point(2)] - step * delta/norm(delta));
        %计算x（k+1）点的梯度值
        delta = subs(grad_f,[x1,x2],[current_point(1),current_point(2)]);
        %计算函数值
        f_value = double(subs(f,[x1,x2],[current_point(1),current_point(2)]));
        %输出迭代计算过程
        result_string=sprintf('k=%d, x1=%.6f, x2=%.6f, step=%.6f f(x1,x2)=%.6f',iterator,current_point(1),current_point(2),step,f_value);
        f1(iterator)=current_point(1);
        f2(iterator)=current_point(2);
        f3(iterator)=f_value;
        disp(result_string);
    end
end

La limitación del algoritmo de gradiente y su optimización

En la red neuronal, la búsqueda de gradiente es el método de optimización de parámetros más utilizado, en este tipo de métodos, a partir de la solución de la estrategia, se busca el valor óptimo del parámetro para cada generación, en cada generación primero se calcula el gradiente de la punto actual de la función establecida y determine la dirección de búsqueda de acuerdo con el gradiente.

Durante el proceso de búsqueda, podemos encontrarnos con el problema de quedar atrapados en un mínimo local, si la función de error tiene múltiples mínimos locales, no se garantiza que la solución encontrada sea el mínimo global, en este último caso, decimos que el parámetro la optimización está atrapada en un mínimo local Minimal, que claramente no era lo que esperábamos.

En tareas reales, las personas suelen utilizar las siguientes estrategias para tratar de "saltar" del mínimo local y acercarse al mínimo global:

Inicialice múltiples redes neuronales con múltiples conjuntos de diferentes valores de parámetros. Después de entrenar de acuerdo con los métodos estándar, tome la solución con el error más pequeño como el parámetro final. Esto es equivalente a comenzar la búsqueda desde múltiples puntos iniciales diferentes, por lo que puede caer en diferentes mínimo local, es posible elegir entre él para obtener un resultado más cercano al mínimo global,
pero también provocará "saltos" del mínimo global
Utilizando la tecnología de "recocido simulado", el recocido simulado acepta un resultado peor que la solución actual con una cierta probabilidad en cada paso, lo que ayuda a "saltar" del mínimo local. Durante cada iteración, acepte "su solución óptima" La probabilidad de disminuirá gradualmente con el tiempo Para garantizar la estabilidad del algoritmo
Use el descenso de gradiente estocástico A diferencia del descenso de gradiente estándar, que calcula los gradientes exactamente, el descenso de gradiente estocástico agrega aleatoriedad al cálculo de gradientes. Por lo tanto, incluso si cae en un mínimo local, el gradiente que calcula aún puede ser distinto de cero, por lo que existe la posibilidad de saltar fuera del mínimo local y continuar buscando.