PSINS toolbox learning (2) Concepto y conversión de matriz de actitud, cuaternión, ángulo de Euler, vector de rotación equivalente

La actitud del portaaviones se refiere a la relación de orientación entre el sistema de coordenadas del portaaviones y el sistema de coordenadas de navegación , y la relación de orientación directa entre los dos sistemas de coordenadas puede ser equivalente al problema de rotación de punto fijo de cuerpo rígido en mecánica . En la teoría de rotación de punto fijo de cuerpos rígidos, los métodos tradicionales para describir la relación de orientación del sistema de coordenadas en movimiento en relación con el sistema de coordenadas de referencia incluyen el método del ángulo de Euler, el método del coseno director y el método del cuaternión . Tanto el método del coseno director tradicional como el método del cuaternión suponen que el cuerpo se mueve con un eje fijo y, en este caso, no hay error de no conmutabilidad . Sin embargo, en el sistema de navegación inercial strapdown, el dispositivo inercial se instala directamente en el cuerpo y sigue el movimiento del cuerpo, por lo que no es adecuado para el entorno real suponer que el movimiento del cuerpo es un eje fijo. para entornos muy dinámicos, existe una solución de actitud de mayor precisión Método de cálculo: método del vector de rotación equivalente .

Dado que el sistema de navegación inercial strapdown adopta la plataforma matemática establecida por el cálculo de la matriz de actitud, en el algoritmo de actualización de la actitud, velocidad y posición del sistema de navegación inercial strapdown, el algoritmo de actitud tiene la mayor influencia en la precisión del conjunto. sistema, y ​​es el punto clave de la investigación y el diseño del algoritmo .

Objetivo de la solución de actitud: conocer los parámetros de actitud iniciales y generar los parámetros de actitud en tiempo real de acuerdo con la medición del giroscopio :

1. Conceptos básicos

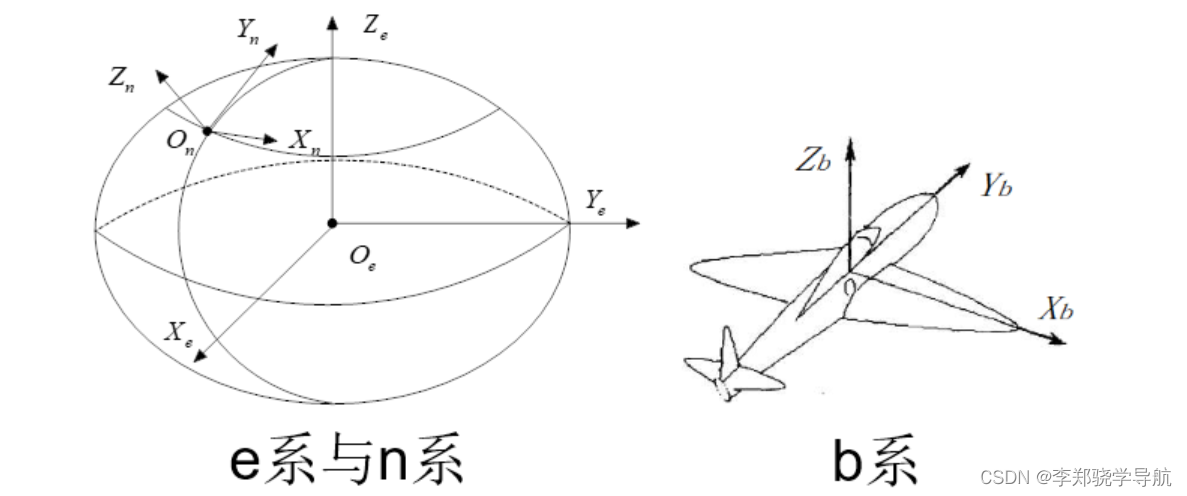
1. Definición de sistema de coordenadas

El sistema de coordenadas de navegación inercial se puede dividir en cuatro categorías según la posición y el eje del origen:

1. Sistema de coordenadas inercial (sistema i)

También conocido como ECI, el origen está en el centro de masa de la tierra y el eje de coordenadas no gira con la tierra (el eje Z apunta al Polo Norte y el eje X apunta al equinoccio vernal). La salida del sensor de inercia se basa en esto. A pesar de verse afectado por el campo gravitatorio del sol, existe $6\ast 10^{-7}g$de fuerza centrípeta orbital; sin embargo, cuando la tierra se usa como referencia de navegación inercial en la superficie de la tierra, el portador en movimiento y la tierra están aproximadamente en el mismo campo gravitatorio solar, y su influencia puede ignorarse.

2. Sistema de coordenadas fijo en la Tierra centrado en la Tierra (sistema e)

También conocido como ECEF, el origen está en el centro de masa del mapa y el eje de coordenadas gira con la tierra (el eje Z apunta al polo norte y el eje X apunta a la intersección del ecuador y el meridiano principal). ). Este sistema de coordenadas es el más utilizado por los sistemas GNSS. El movimiento angular de ECEF relativo a ECI es la tasa angular de rotación de la tierra ${Vaya}_{yo}$。

3. Sistema de coordenadas de navegación (sistema n)

También conocido como sistema local de coordenadas horizontales, el origen está en la portadora y el eje de coordenadas no cambia con la portadora . Hay dos descripciones: North East Earth (NED) y North East Heaven (ENU). Es el sistema de coordenadas utilizado por la navegación inercial para resolver los parámetros.El cálculo de la navegación inercial se preocupa especialmente por la aceleración de la gravedad, que se puede mostrar en este sistema de coordenadas.

4. Sistema de coordenadas de transporte (sistema b)

El origen está en la portadora y el eje de coordenadas cambia con la portadora . En comparación con el sistema de coordenadas de navegación, también hay dos descripciones: frontal inferior derecha (FRD) y frontal superior derecha (RFU). Hay muchas series b en un sistema de navegación: serie b de IMU, serie b de soporte, serie b de cámara, etc. La relación de acimut entre el sistema b y el sistema i se puede describir mediante un conjunto de ángulos de Euler.

En PSINS: sistema de coordenadas de navegación (n): este E-norte N-día U, sistema de coordenadas del vehículo (b): derecha R-frente F-arriba U

2. Matriz antisimétrica

$$(V\times )=\left[\begin{array}{ccc}0& -V_{}& V_{}\\ V_{}& 0& -V_{}\\ -V_{}& V_{}& \end{array}\right]$$

puntos de antisimetría：

1. Ambos son 0 en la diagonal, y las partes superior e inferior son simétricas y opuestas, es decir: $(V\times )=-(V\times {)}^T$ , por lo que se llama matriz antisimétrica.

2. El producto cruzado de un vector por otro vector es igual al producto puntual de la matriz antisimétrica de otro vector, y el producto cruzado se convierte en producto puntual .

3. 反对称阵的幂方通式：
   $$(V\times {)}^i=\{\begin{array}{ll}(-1)\_{}^{(yo-1)/}{2v}^{yo-1}(V\times )& i=1,3,5,\cdots \\ (-1)\_{}^{(yo-2)/}{2v}^{yo-2}(V\times {)}^{}& i=2,4,6,\end{array}$$

3. Ángulo de Euler

$$A={\left[\begin{array}{lll}& & \end{array}\right]}^T$$

El ángulo de Euler es un método clásico para describir la actitud relativa entre dos sistemas de coordenadas por el ángulo transformado alrededor del eje de coordenadas El significado físico es intuitivo y fácil de entender, especialmente para describir el movimiento del sistema de coordenadas del portador en relación con la coordenada de navegación local sistema _

Los ángulos de Euler representan la rotación : en el espacio tridimensional, la relación de orientación de un sistema de coordenadas rectangulares en relación con otro sistema de coordenadas rectangulares puede describirse mediante tres rotaciones secuenciales , y el eje de coordenadas alrededor de cada rotación es ortogonal a los ejes de rotación frontal y posterior. Euler demostró que la relación de orientación relativa entre dos sistemas de coordenadas ortogonales cualquiera puede describirse mediante un conjunto de ángulos no menor de 3, y los ángulos de rotación de estas tres rotaciones se denominan conjunto de ángulos de Euler (grupo de ángulos de Euler ) .

Los ángulos de Euler representan la actitud : para describir la actitud del portador, puede especificar un sistema de coordenadas de referencia y luego usar un conjunto de ángulos de Euler para describir la rotación del sistema de coordenadas que está conectado al portador y el sólido en relación con el sistema de coordenadas de referencia. En las aplicaciones de navegación cerca de la Tierra, el sistema de coordenadas de referencia generalmente selecciona el sistema de coordenadas geográficas local por defecto, mientras que el sistema de coordenadas en movimiento es un sistema de coordenadas conectado de forma fija al vehículo.

• Ángulo de curso : El ángulo incluido entre la proyección del eje longitudinal positivo de la portadora en el plano horizontal local y la dirección del norte geográfico local. A menudo se toma como positivo de norte a este, generalmente representado por ψ, y el rango del ángulo es 0 ∼ 360◦ o −180◦ ∼ +180◦ .
• Ángulo de cabeceo : el ángulo entre la dirección positiva del eje longitudinal del portador y su línea de proyección horizontal, se define como positivo cuando el portador "levanta la cabeza", generalmente representado por θ, y su valor oscila entre −90◦ y 90◦.
• Ángulo de balanceo : el ángulo entre la dirección positiva del eje vertical del portaaviones y el plano vertical donde se encuentra el eje longitudinal del portaaviones.Cuando el portaaviones se inclina hacia la derecha (como cuando se presiona hacia abajo el ala derecha del avión) , es positivo Use ϕ \ $\varphi$ indica que el rango de valores es −180◦ ∼ +180◦.

Fundamentos de los ángulos de Euler：

1. La relación de orientación relativa entre dos sistemas de coordenadas ortogonales se puede describir mediante un conjunto de ángulos de Euler, dado un conjunto de ángulos de Euler, la secuencia de ejes de rotación correspondiente debe especificarse al mismo tiempo. PSINS usa el cielo del noreste, 312 ángulos de Euler
2. El ángulo de actitud de navegación, incluido el ángulo de rumbo, el ángulo de cabeceo y el ángulo de balanceo, está estrechamente relacionado con el eje físico del vehículo y no tiene nada que ver con el sistema de coordenadas matemáticas seleccionado del vehículo.
3. Cuando el ángulo de inclinación es $\pm 90^{Cuando\; \circ }$ , hay un valor singular en la transformación del ángulo de Euler, y el ángulo de balanceo y el ángulo de rumbo no se pueden distinguir en este momento. Por lo tanto, el método del ángulo de Euler no se puede utilizar para aplicaciones de navegación de actitud completa.
4. Los conjuntos de ángulos de Euler no se pueden sumar directamente para representar la composición de dos rotaciones.

4. Matriz de rotación/matriz de coseno director

$$C=\left[\begin{array}{lll}{C}_{}& C_x& C_x\\ C_y& C_{}& C_{}\\ C_z& C_{}& C_{}\end{array}\right]$$

La matriz de coseno director (Direction Cosine Matrix, DCM) es una matriz de actitud representada por el coseno director del vector, que a menudo se usa para describir la actitud relativa de dos sistemas de coordenadas. En comparación con los ángulos de Euler, la matriz de coseno director es mucho más abstracta, pero es muy conveniente para manejar la transformación de proyección de vectores .

Sabemos que los tres valores de proyección del vector en el espacio son las coordenadas, y el mismo vector está en $i$ serie y$El$ sistema b tiene dos conjuntos de coordenadas, y su relación se puede expresar como:
$$V=V_X^{}{i}_{}+V_y^{}{j}_{}+V_z^{}{k}_{}=V_X^{}{i}_{}+V_y^{}{j}_{}+V_z^{}{k}_{}$$
即$\left[\begin{array}{lll}{i}_{}& j_{}& k_{}\end{array}\right]\left[\begin{array}{c}{V}_X^{}\\ V_y^{}\\ V_z^{}\end{array}\right]=\left[\begin{array}{lll}{i}_{}& j_{}& k_{}\end{array}\right]\left[\begin{array}{c}{V}_X^{}\\ V_y^{}\\ V_z^{}\end{array}\right]=\left[\begin{array}{lll}{i}_{}& j_{}& k_{}\end{array}\right]PAG\left[\begin{array}{c}{V}_X^{}\\ V_y^{}\\ V_z^{}\end{array}\right]$

有：
$$\left[\begin{array}{c}{V}_X^{}\\ V_y^{}\\ V_z^{}\end{array}\right]=PAG\left[\begin{array}{c}{V}_X^{}\\ V_y^{}\\ V_z^{}\end{array}\right]$$
记为$V^i=PV{\_}^b=C_b^{}{V}^b$，$C_b^{}$Se llama matriz de transformación del sistema de coordenadas (i->b) o matriz de transformación de coordenadas (b->i), también conocida como matriz de coseno director y matriz de transición .

Aspectos básicos de la matriz de coseno de dirección：

1. Dado que todos son matrices de unidades, cada elemento en la matriz de coseno de dirección representa el valor del coseno del ángulo entre los ejes de coordenadas de los dos conjuntos de sistemas de coordenadas, de ahí el nombre.
2. Distinga entre la matriz de transformación del sistema de coordenadas y la matriz de transformación de coordenadas .
3. Aunque la matriz del coseno director tiene 9 parámetros, contiene 6 restricciones, es decir, el módulo del vector fila es 1 y cada par es ortogonal, y solo 3 parámetros son independientes.
4. 方向余弦矩阵是正交矩阵, ${\left({\mathbf{C}}_{\alpha }^{\beta }\right)}^{-1}={\left({\mathbf{C}}_{\alpha }^{\beta }\right)}^{\mathrm{T}}$ 。多次连续转动可以用相应的多个方向余弦矩阵连乘来表示: ${\mathbf{C}}_a^d={\mathbf{C}}_b^d{\mathbf{C}}_a^b$ 。
5. 当载体运动时，两个坐标系之间的相对姿态随时间变化，对应的方向余弦矩阵 ${\mathbf{C}}_b^R(t)$ 则是 一个时变矩阵, 其微分方程为 ${\dot{\mathrm{C}}}_b^R={\mathbf{C}}_b^R\left({\mathbf{\omega }}_{Rb}^b\times \right)$。
6. El método de iteración de Picard se puede utilizar para resolver la ecuación diferencial de la matriz del coseno director, y se obtiene una serie representada por una integral repetida infinitamente, que también se denomina serie de Picard. La serie anterior es cerrada, pero solo en el " fijo rotación del eje " Solo en un caso especial se puede obtener la solución cerrada de la siguiente forma: $C_b^{}\left(t\right)=do\left(0\right)\mathrm{Exp}\left({\int }_0^{}\Omega \left(\tau \right)re\tau \right)$ .
7. 姿态手机公式：$C_{b\left(k\right)}^{}=C_{segundo(k-1)}^{}{C}_{b\left(k\right)}^{segundo(k-1}$, $C_{b\left(k\right)}^{segundo(k-1}=I+\frac{pecado\_\_yo{\_}_{}}{yo{\_}_{}}\left[D{yo}_{}\times \right]+\frac{1-cos\_yo{\_}_{}}{yo{\_}_k^{}}{\left[D{yo}_{}\times \right]}^2$
8. Para aplicaciones comunes de navegación inercial, $La\; suposición\; de\; rotación\; de\; eje\; fijo\; del\; sistema\; b$ generalmente no es válidaCuando esta condición no se cumple, el incremento de ángulo generado por el giróscopo todavía se aplica a la fórmula para el cálculo recursivo de la actualización de actitud, lo que conducirá a unaProblema irreversible en la solución de actualización de actitud Error sexual,el vector de rotación equivalente se puede utilizar para resolver este problema.

5. Cuaterniones

$$q=q_{}+q_{}i+q_{}j+q_{}k=q_{}+q_{}$$

Sabemos que los números complejos se pueden considerar como vectores en el plano complejo, es decir, un vector bidimensional, ampliando el concepto de números complejos, se pueden obtener cuaterniones para describir vectores en el espacio tridimensional.

Esenciales del cuaternión：

1. Los cuaterniones tienen principalmente las siguientes representaciones: $q=q_{}+q_{}i+q_{}j+q_{}k$ , forma de coordenadas vectoriales$q={\left[q_{},q_{},q_{},q_{}\right]}^T$、$q=q_{}+q_{}$O la forma trigonométrica $q=\mathrm{porque}\frac{}{2}+tu\mathrm{pecado}\frac{}{2}$(Está relacionado con el vector de rotación equivalente, normalizado, y el módulo es uno)

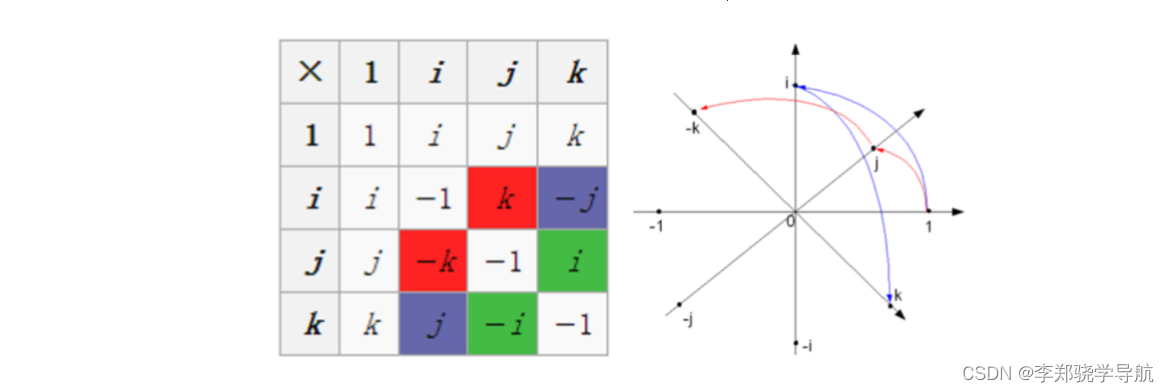
2. La multiplicación entre unidades imaginarias de cuaternión tiene las siguientes características: cuando la unidad se multiplica por sí misma, el rendimiento es el mismo que el de los números complejos, y la multiplicación entre dos pares es igual al producto exterior (producto cruzado) de tres -vectores dimensionales.
   $$\{\begin{array}{l}i\circ i=j\circ j=k\circ k=-1\\ i\circ j=k,j\circ k=yo,k\circ i=j,j\circ i=-k,\_k\circ j=-yo,i\circ k=-\end{array}$$

3. La transformación de coordenadas del vector tridimensional se puede realizar utilizando el operador de transformación de rotación del cuaternión: $v^R=q_b^{}\circ v^b\circ q_b^{R^{}}$。

4. Unidad de notación trigonométrica de cuaterniones : $q=q_{}+q_{}=\mathrm{porque}\frac{}{2}+tu\mathrm{pecado}\frac{}{2}$tiene un claro significado físico. A menudo agrega un subíndice a la derecha del cuaternión, escrito como $q_b^{}$，中$u$ representa el sistema de coordenadas en movimiento ($b$ ) relativo al sistema de coordenadas de referencia ($i$ system) el eje unitario de rotación,$\varphi$ indica el tamaño del ángulo de rotación,$\varphi u$ representa el vector de rotación equivalente. Después de usar subíndices, el cuaternión conjugado se puede escribir como$q_i^{}={\left(Q_b^{}\right)}^{\ast }$ , que es similar a la representación de la transposición de matrices, como$C_i^{}={\left(C_b^{}\right)}^{T.}$ _

5. Ecuación diferencial para cuaterniones: $q_b^{}=\frac{}{2}{q}_b^{}\circ \left[\begin{array}{c}0\\ {Vaya}_{Rb\_}^{}\end{array}\right]$ , o en forma de matriz:$q_b^{}=\frac{}{2}W{q}_b^{}$. Así, se establece la relación entre el cuaternión y la velocidad angular de rotación.

6. Resolver ecuaciones diferenciales para cuaterniones, cuando $Cuando\; el\; sistema\; b$ satisface la condición de "rotación de eje fijo", se puede obtener la solución analítica:$q_b^{}\left(t\right)=$ $\left[yo\mathrm{porque}\frac{yo}{2}+\frac{}{yo\_}\mathrm{pecado}\frac{yo}{2}\right]q_b^{}\left(0\right)$。

7. También hay octoniones, que se utilizan para describir el movimiento en espiral, el movimiento de alambre y el movimiento angular.

6. Vector de rotación equivalente

Euler propuso por primera vez el concepto de vector de rotación equivalente al estudiar el movimiento de los cuerpos rígidos. Señaló que cualquier rotación finita de punto fijo de un cuerpo rígido puede realizarse de manera equivalente mediante una rotación alrededor de un eje que pasa por el punto fijo . Y se establece la fórmula de transformación del vector unitario sobre el cuerpo rígido antes y después de la rotación. La clave para la investigación del moderno algoritmo de actualización de actitud de navegación inercial strapdown es cómo utilizar el valor medido del giroscopio para construir el vector de rotación equivalente correspondiente , a fin de minimizar o eliminar el error no intercambiable en el algoritmo de actualización de actitud . El uso subsiguiente del vector de rotación equivalente para calcular el cambio de actitud, tal como se expresa mediante una matriz de coseno director o un cuaternión, será muy simple.

Use los valores de muestreo de varios incrementos angulares para calcular un vector de rotación equivalente de acuerdo con varios algoritmos de muestra y luego use el vector de rotación equivalente calculado para actualizar la matriz de coseno de dirección y el cuaternión.

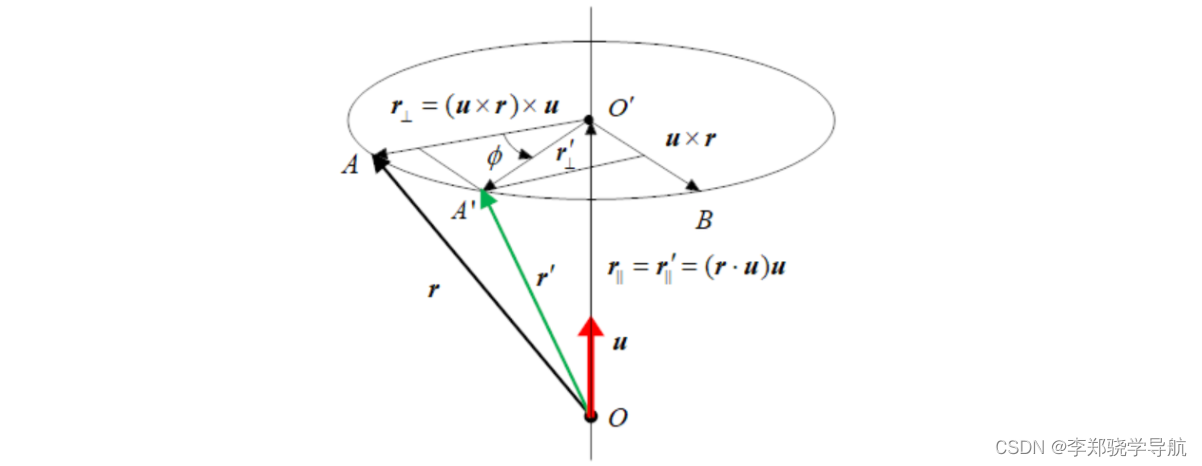
vector espacial $r$ Vector de eje de rotación$rotas$ ϕ$\varphi$ , el vector r ′ r^{'}obtenido por rotación$r^{{}^{\text{'}}}$ . Las cuatro cantidades deben tener directamente una relación funcional$r^{{}^{\prime }}=f(r,tu,\varphi )$，利用一些几何关系，可以推导得到：
$$\begin{array}{rl}{r}^{\prime }& =(tu\cdot r)tu+(tu\times r)\times tu\mathrm{porque}\varphi +tu\times r\mathrm{pecado}\varphi \\ & =\left[yo+(tu\times {)}^2\right]r-(tu\times {)}^{2r}\_\mathrm{porque}\varphi +tu\times r\mathrm{pecado}\varphi \\ & =\left[yo+\mathrm{pecado}\varphi (tu\times )+(1-\mathrm{porque}\varphi )(tu\times {)}^2\right]r=dr\end{array}$$
可记$D=I+\mathrm{pecado}\varphi (tu\times )+(1-\mathrm{porque}\varphi )(tu\times {)}^2$ , esta fórmula se llamafórmula de rotación de Rodrigue;$r^{\text{'}}$ ir arrLa matriz multiplicada por$r$ se denomina matriz de rotación de Rodriguey el eje de rotación$u$ y ángulo de rotación$\varphi$ está relacionado.

Aplicando la fórmula de rotación de Rodrigue al eje de coordenadas unitarias del sistema de coordenadas cartesianas, el sistema de coordenadas de referencia se puede transferir al sistema de coordenadas en movimiento: ib =
D iijb = D jikb = D ki } \left.\begin{array}{c} \ boldsymbol{i}_{b}=\boldsymbol{D} \boldsymbol{i}_{i} \\ \boldsymbol{j}_{b}=\boldsymbol{D} \boldsymbol{j}_{i} \ \ \boldsymbol{k}_{b}=\boldsymbol{D} \boldsymbol{k}_{i}\end{matriz}\right\}isegundo=Di _yojsegundo=DJ _yoksegundo=re kyo​⎭ ⎬ ⎫

$$\{\begin{array}{c}Relación\; de\; transformación\; de\; rotación\; base:\left[\begin{array}{lll}{i}_{}& j_{}& k_{}\end{array}\right]=D\left[\begin{array}{lll}{i}_{}& j_{}& k_{}\end{array}\right]\\ Relación\; de\; transformación\; de\; proyección\; base:\left[\begin{array}{lll}{i}_{}& j_{}& k_{}\end{array}\right]=\left[\begin{array}{lll}{i}_{}& j_{}& k_{}\end{array}\right]\end{array}$$

$$Proyecciónenel\; sistema\; i\; :\begin{array}{l}\left[\begin{array}{lll}{i}_b^i& {\mathbf{j}}_b^i& {\mathbf{k}}_b^i\end{array}\right]=\mathbf{D}\left[\begin{array}{lll}{\mathbf{i}}_i^i& {\mathbf{j}}_i^i& {\mathbf{k}}_i^i\end{array}\right]=\mathbf{D}\mathbf{I}\\ \left[\begin{array}{lll}{\mathbf{i}}_b^i& {\mathbf{j}}_b^i& {\mathbf{k}}_b^i\end{array}\right]=\left[\begin{array}{lll}{\mathbf{i}}_i^i& {\mathbf{j}}_i^i& {\mathbf{k}}_i^i\end{array}\right]\mathbf{P}=\mathbf{IP}\end{array}\}\mathbf{D}=\mathbf{P}={\mathbf{C}}_b^i$$

$P=D$ 表明，罗德里格旋转矩阵 $D$ 正好是从参考坐标系（$i$ 系）到动坐标系（$b$ 系）的过渡矩阵，它也是从 $b$ 系到 $i$ 系的坐标变换矩阵。因此可以将罗德里格旋转公式重新写为方向阵的形式：
$${\mathbf{C}}_b^i=\mathbf{I}+\sin \varphi (\mathbf{u}\times )+(1-\cos \varphi )(\mathbf{u}\times {)}^2$$
进一步, 若记 $\mathbf{\varphi }=\varphi \mathbf{u}$ 和 $\varphi =|\mathbf{\varphi }|$, 则有 $\mathbf{u}=\mathbf{\varphi }/\varphi$ ，得：
$${\mathbf{C}}_b^i=\mathbf{I}+\frac{\sin \varphi }{\varphi }(\mathbf{\varphi }\times )+\frac{1-\cos \varphi }{{\varphi }^2}(\mathbf{\varphi }\times {)}^2$$
这里 $\mathbf{\varphi }$ 称为等效旋转矢量（RV，简称旋转矢量）

等效旋转矢量要点：

1. 刚体的有限转动是不可交换的。刚体的定点有限旋转都可以用绕经过该固定点的一个轴的一次转动来实现。
2. 其矢量方向表示旋转的方向，模的大小表示旋转角度大小。
3. 当载体的角速度方向随时间变化而不是做 “定轴转动” 时, 直接将传感器角增量测量值代入方向余弦矩阵或四元数微分方程的求解计算式中，则会带来 “不可交换性误差”。
4. Bortz 方程： $\dot{\varphi }=\mathbf{\omega }+\frac{1}{2}(\varphi \times \omega )+\frac{1}{{\varphi }^2}\left[1-\frac{\varphi \sin \varphi }{2(1-\cos \varphi )}\right]\mathbf{\varphi }\times (\mathbf{\varphi }\times \mathbf{\omega })$ 。是一种常用的等效旋转矢量微分方程，利用等效旋转矢量进行转动不可交换误差补偿。
5. 等效旋转矢量的双子样求解式：${\varphi }_k=\Delta {\theta }_k+\frac{1}{12}\Delta {\theta }_{k-1}\times \Delta {\theta }_k$ 。

二、PSINS中的表示转换

1、姿态阵/姿态四元数/欧拉角的表示 Cnb/qnb/att

• 有角标的符号书写一般遵从规律是从左到右从上到下。

• 姿态阵：Cnb，表示从 b 系到 n 系的坐标变换矩阵。对应姿态四元数写为qnb。

• 欧拉角：att=[俯仰pitch; 横滚roll; 方位yaw]。没有按照转到顺序来写，如果按转动顺序，东北天坐标系转到右前下坐标系，常见先转方位角、然后俯仰角、横滚角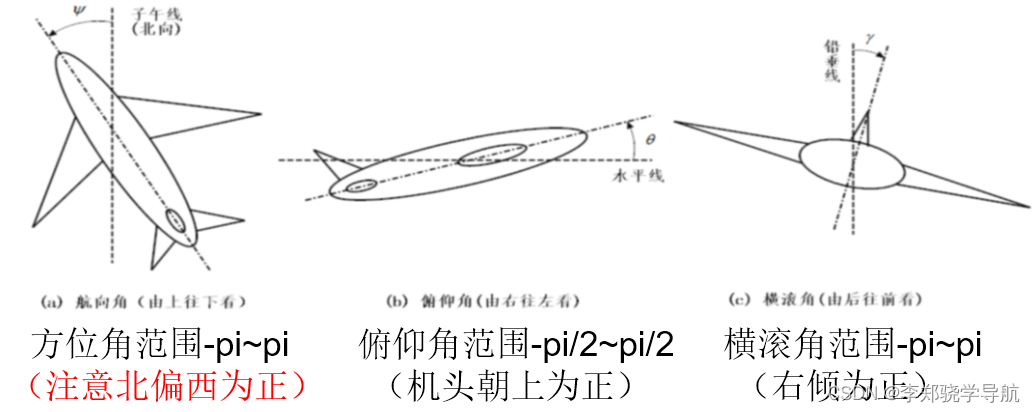

  

2、四元数计算

1. 四元数共轭：qconj

实部不变，虚部取反。

function qo = qconj(qi)
    qo = [qi(1); -qi(2:4)];

性质：

• 加的共轭等于共轭的加：$(\mathbf{P}+Q{)}^{\ast }=P^{\ast }+Q^{\ast }$
• 乘的共轭等于共轭的和：$(\mathbf{P}\circ Q{)}^{\ast }=Q^{\ast }\circ P^{\ast }$

2. 四元数归一化：qconj

function qnb = qnormlz(qnb)
    qnb = qnb/norm(qnb);

3. Multiplicación de cuaterniones: qmual

$$\{\begin{array}{l}i\circ i=j\circ j=k\circ k=-1\\ i\circ j=k,j\circ k=yo,k\circ i=j,j\circ i=-k,\_k\circ j=-yo,i\circ k=-\end{array}$$

El tipo de cambio no se cumple. $i、j、k$ 正向相乘等于后面一项，反向相乘要加负号。

function q = qmul(q1, q2)
    if length(q2)==3, q2=[0; q2]; end  % 0-scale quaternion
    q = [ q1(1) * q2(1) - q1(2) * q2(2) - q1(3) * q2(3) - q1(4) * q2(4);
          q1(1) * q2(2) + q1(2) * q2(1) + q1(3) * q2(4) - q1(4) * q2(3);
          q1(1) * q2(3) + q1(3) * q2(1) + q1(4) * q2(2) - q1(2) * q2(4);
          q1(1) * q2(4) + q1(4) * q2(1) + q1(2) * q2(3) - q1(3) * q2(2) ];

AI解释：
这个函数实现了两个四元数的乘法操作。四元数是一种用于表示旋转和仿射变换的数学对象。在这个函数中，q1和q2是两个四元数，函数将它们相乘，并将结果存储在变量q中。

1. 首先，函数会检查q2的长度是否为3。如果是，它会将q2扩展为长度为4的四元数，其中一个元素被设置为0。这是为了避免在后续计算中出现除以0的情况。
2. 接下来，函数通过使用四元数的乘法公式来计算结果。四元数的乘法可以通过将两个四元数的各个分量对应相乘，然后将乘积相加得到。
3. 最后，函数将计算得到的结果存储在变量q中，并返回该变量作为函数输出。

4. 四元数乘向量（三维向量的坐标变换）：qmulv

假设一个三维矢量 $r$，在载体坐标系（$b$ 系）和参考坐标系（$i$ 系）中的投影分别为：${\mathbf{r}}^b={\left[\begin{array}{lll}{r}_x^b& r_y^b& r_z^b\end{array}\right]}^T$和$r^i={\left[\begin{array}{lll}{r}_X^{}& r_y^{}& r_z^{}\end{array}\right]}^T$ , ahora para el vector$r^b$ (tratado como un cuaternión escalar cero) implementa la siguiente operación de multiplicación de cuaterniones:
$$\begin{array}{rl}{q}_b^{}\circ r^b\circ q_i^{}=& {METRO}_{q_b^{}}\left(r^b\circ q_i^{}\right)={METRO}_{q_b^{}}\left(M_{q_i^{}}^{}\left[\begin{array}{c}0\\ r^{}\end{array}\right]\right)={METRO}_{q_b^{}}{METRO}_{q_i^{}}^{}\left[\begin{array}{c}0\\ r^{}\end{array}\right]=\\ & \left[\begin{array}{cccc}{q}_{}& -q_{}& -q_{}& -q_{}\\ q_{}& q_{}& -q_{}& q_{}\\ q_{}& q_{}& q_{}& -q_{}\\ q_{}& -q_{}& q_{}& q_{}\end{array}\right]\left[\begin{array}{cccc}{q}_{}& q_{}& q_{}& q_{}\\ -q_{}& q_{}& -q_{}& q_{}\\ -q_{}& q_{}& q_{}& -q_{}\\ -q_{}& -q_{}& q_{}& q_{}\end{array}\right]\left[\begin{array}{c}0\\ r_X^{}\\ r_y^{}\\ r_z^{}\end{array}\right]=\\ & \left[\begin{array}{cccc}1& 0& 0& 0\\ 0& q_0^{}+q_1^{}-q_2^{}-q_3^{}& 2\left(q_{}{q}_{}-q_{}{q}_{}\right)& 2\left(q_{}{q}_{}+q_{}{q}_{}\right)\\ 0& 2\left(q_{}{q}_{}+q_{}{q}_{}\right)& q_0^{}-q_1^{}+q_2^{}-q_3^{}& 2\left(q_{}{q}_{}-q_{}{q}_{}\right)\\ & 2(q_{}{q}_{}-q_{}{q}_{}& 2(q_{}{q}_{}+q_{}{q}_{}& q_0^{}-q_1^{}-q_2^{}+q_3^{}\end{array}\right]\left[\begin{array}{c}0\\ r_X^{}\\ r_y^{}\\ r_z^{}\end{array}\right]\end{array}$$
Se puede encontrar que la matriz de bloque diagonal de tercer orden en la esquina inferior derecha de la matriz es exactamente la matriz de actitud, que se puede abreviar como:
$$q_b^{}\circ r^b\circ q_i^{}=\left[\begin{array}{cc}1& 0_{1\times }\\ 0_{3\times }& C_b^{}\end{array}\right]\left[\begin{array}{c}0\\ r^{}\end{array}\right]=\left[\begin{array}{c}0\\ C_b^{}{r}^{}\end{array}\right]=\left[\begin{array}{c}0\\ r^{}\end{array}\right]$$
Esto muestra que$q_b^{}\circ r^b\circ q_i^{}$El resultado de es también un cuaternión escalar cero cuya parte imaginaria corresponde exactamente a la transformación de coordenadas $r^i=C_b^{}{r}^{segundo}$ _ Para escribir de manera concisa, similar al hábito de expresión de transformación de coordenadas de la matriz, se puede definir la operación de multiplicación entre el cuaternión y el vector tridimensional, es decir, la fórmula de transformación de coordenadas del cuaternión: ri = Q bi ⊗ rbr^{ i}
$$r^i=q_b^{}\otimes r^{El\; significado\; de\; b}$$
es realizar primero la multiplicación de cuaterniones y luego extraer la parte imaginaria del resultado.

function vo = qmulv(q, vi)
    qo1 =              - q(2) * vi(1) - q(3) * vi(2) - q(4) * vi(3);
    qo2 = q(1) * vi(1)                + q(3) * vi(3) - q(4) * vi(2);
    qo3 = q(1) * vi(2)                + q(4) * vi(1) - q(2) * vi(3);
    qo4 = q(1) * vi(3)                + q(2) * vi(2) - q(3) * vi(1);
    vo = vi;
    vo(1) = -qo1 * q(2) + qo2 * q(1) - qo3 * q(4) + qo4 * q(3);
    vo(2) = -qo1 * q(3) + qo3 * q(1) - qo4 * q(2) + qo2 * q(4);
    vo(3) = -qo1 * q(4) + qo4 * q(1) - qo2 * q(3) + qo3 * q(2);

5. Quaternion más error de ángulo de desalineación: qaddphi

Desde el sistema de navegación real ( $n$ sistema) al sistema de navegación computacional (${norte}^{\prime }$ system) el ángulo de desalineación es$\varphi$ , por el contrario, de${norte}^{\text{'}}$ está vinculado annEl ángulo de desalineación del$sistema\; n$$-\varphi$ , si$-\varphi$ se considera un vector de rotación equivalente, entonces el cuaternión de transformación correspondiente es$q_{norte}^{{norte}^{}}$. En el programa, las variables qpb, , qnbrepresentan phiQ $q_b^{{norte}^{}},q_b^{}$y $\varphi$ _

function qpb = qaddphi(qnb, phi)
    qpb = qmul(rv2q(-phi),qnb);

6. Cuaternión menos error de desalineación: qdelphi

Correspondiente a la fórmula $q_b^{}=q_{{norte}^{\prime }}^{}{}^{\circ }{Q}_b^{}$, lo que significa: Después de deducir el ángulo de desalineación en el cálculo del cuaternión de actitud, se obtiene el cuaternión de actitud real (más preciso).

function qnb = qdelphi(qpb, phi)
    qnb = qmul(rv2q(phi), qpb);

7. Calcule el error del ángulo de desalineación del cuaternión y el cuaternión real: qq2phi

Primero, según la fórmula $q_{{norte}^{\prime }}^{}=q_b^{}\circ \left(Q_b^{{norte}^{}}\right){}^{\ast }$ Obtener el cuaternión de error$q_{{norte}^{\prime }}^{}$, y luego por $q_{{norte}^{\prime }}^{}$Resolviendo para el ángulo de desalineación $\varphi$ _

function phi = qq2phi(qpb, qnb)
    qnp = qmul(qnb, qconj(qpb));
    phi = q2rv(qnp);

3. Conversión de varias representaciones de gestos

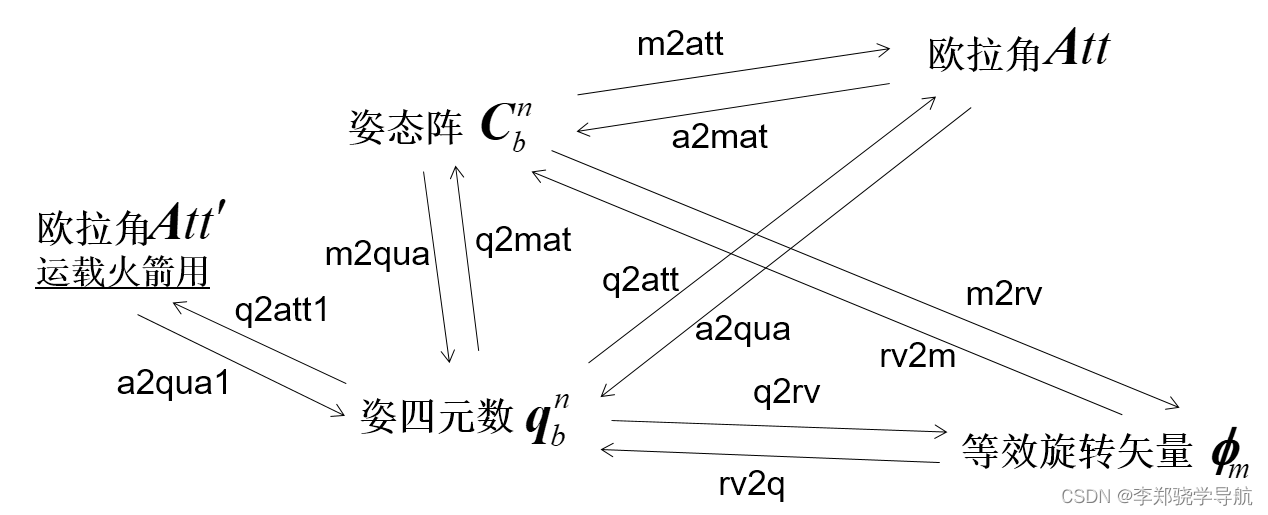
1. Ángulo de Euler -> matriz de actitud: a2mat

El ángulo de Euler usa tres selecciones para representar el cambio de actitud, y las tres matrices de selección se multiplican para obtener la matriz del coseno director (matriz de actitud), y el orden de rotación es crítico.
$$\begin{array}{l}{C}_b^{}=C_{}{C}_{}{C}_{}=\left[\begin{array}{ccc}{C}_{}& -s_{}& 0\\ s_{pag}& C_{}& 0\\ & & \end{array}\right]\left[\begin{array}{ccc}1& 0& 0\\ 0& C_{}& -s_{}\\ & s_{}& C_{}\end{array}\right]\left[\begin{array}{ccc}{C}_{}& 0& s_{}\\ 0& 1& 0\\ -s_{}& & C_{}\end{array}\right]=\\ \left[\begin{array}{ccc}{C}_{}{C}_{}-s_{}{s}_{}{s}_{}& -s_{}{C}_{}& C_{}{s}_{}+s_{}{s}_{}{C}_{}\\ s_{}{C}_{}+C_{}{s}_{}{s}_{}& C_{}{C}_{}& s_{}{s}_{}-C_{}{s}_{}{C}_{}\\ -c_{}{s}_{}& s_{}& C_{}{C}_{}\end{array}\right]=\left[\begin{array}{ccc}{C}_{}& C_{}& C_{}\\ C_{}& C_{}& C_{}\\ C_{}& C_{}& C_{}\end{array}\right]\end{array}$$

function [Cnb, Cnbr] = a2mat(att)
% Convert Euler angles to direction cosine matrix(DCM).
% 欧拉角->姿态阵
% Prototype: [Cnb, Cnbr] = a2mat(att)
% Input: att - att=[pitch; roll; yaw] in radians
% Outputs: Cnb - DCM from navigation-frame(n) to body-frame(b), in yaw->pitch->roll
%                (3-1-2) rotation sequence
%          Cnbr - DCM in yaw->roll->pitch (3-2-1) rotation sequence
    s = sin(att); c = cos(att);
    si = s(1); sj = s(2); sk = s(3); 
    ci = c(1); cj = c(2); ck = c(3);
    Cnb = [ cj*ck-si*sj*sk, -ci*sk,  sj*ck+si*cj*sk;
            cj*sk+si*sj*ck,  ci*ck,  sj*sk-si*cj*ck;
           -ci*sj,           si,     ci*cj           ];
    if nargout==2  % dual Euler angle DCM
        Cnbr = [ cj*ck, si*sj*ck-ci*sk, ci*sj*ck+si*sk;
                 cj*sk, si*sj*sk+ci*ck, ci*sj*sk-si*ck;
                -sj,    si*cj,          ci*cj            ];
    endfunction [Cnb, Cnbr] = a2mat(att)
    s = sin(att); c = cos(att);
    si = s(1); sj = s(2); sk = s(3); 
    ci = c(1); cj = c(2); ck = c(3);
    Cnb = [ cj*ck-si*sj*sk, -ci*sk,  sj*ck+si*cj*sk;
            cj*sk+si*sj*ck,  ci*ck,  sj*sk-si*cj*ck;
           -ci*sj,           si,     ci*cj           ];
    if nargout==2  % dual Euler angle DCM
        Cnbr = [ cj*ck, si*sj*ck-ci*sk, ci*sj*ck+si*sk;
                 cj*sk, si*sj*sk+ci*ck, ci*sj*sk-si*ck;
                -sj,    si*cj,          ci*cj            ];
    end

Explicación de AI :
este código es una función que convierte los ángulos de Euler en una matriz de pose. Genera dos parámetros de salida: Cnb y Cnbr, que representan respectivamente la matriz de actitud del sistema de navegación al sistema de la aeronave y otra matriz de actitud del sistema de navegación al sistema de la aeronave. Si el número de parámetros de salida de la función es 2 (es decir, se requiere que Cnb y Cnbr se generen al mismo tiempo), también se calculará la matriz Cnbr. La matriz Cnbr está construida en un orden de rotación "guiñada-alabeo-cabeceo" (3-2-1).

2. Matriz de actitud -> ángulo de Euler: m2att

$$\begin{array}{l}\theta =\arcsin \left(C_{32}\right)\\ \{\begin{array}{l}\gamma =-\mathrm{atan}2\left(C_{31},C_{33}\right)\\ \psi =-\mathrm{atan}2\left(C_{12},C_{22}\right)\end{array}\left|C_{32}\right|⩽0.999999\\ \{\begin{array}{ll}\gamma =\mathrm{atan}2\left(C_{13},C_{}\right)& |C_{}|>\mathrm{0.999.999}\\ pag=& \end{array}\end{array}$$

function [att, attr] = m2att(Cnb)
% Convert direction cosine matrix(DCM) to Euler attitude angles.
% 姿态阵 -> 欧拉角
% Prototype: [att, attr] = m2att(Cnb)
% Input: Cnb - DCM from navigation-frame(n) to body-frame(b)
% Outputs: att - att=[pitch; roll; yaw] in radians, in yaw->pitch->roll
    att = [ asin(Cnb(3,2));
            atan2(-Cnb(3,1),Cnb(3,3)); 
            atan2(-Cnb(1,2),Cnb(2,2)) ];
    if nargout==2  % dual Euler angles
        attr = [ atan2(Cnb(3,2),Cnb(3,3)); 
                 asin(-Cnb(3,1)); 
                 atan2(Cnb(2,1),Cnb(1,1)) ];
    end

AI Explicación :
este código es una función de MATLAB para convertir la matriz de coseno de dirección (DCM) en ángulo de actitud de Euler. El nombre de la función es m2att, el parámetro de entrada es la matriz DCM Cnb, el parámetro de salida es el ángulo de actitud de Euler att y el eje de rotación opcional y el ángulo de rotación attr. La función del código es la siguiente:

1. Exprese cada columna de la matriz Cnb de DCM como un vector unitario que representa el vector de rotación desde el sistema de coordenadas de navegación (n) hasta el sistema de coordenadas del cuerpo (b).
2. Utilice estos vectores de rotación para calcular la pose del marco del cuerpo en relación con el marco de navegación, lo que da como resultado ángulos de pose de Euler.
3. Almacene el ángulo de actitud de Euler calculado en la matriz att, organizado en el orden de guiñada -> cabeceo -> balanceo, en radianes.
4. Si el parámetro de salida attr se especifica en forma de ángulos de Euler dobles (juzgando el valor de la variable nargout), también es necesario calcular el eje de rotación y el ángulo de rotación.
5. La fórmula para calcular el eje de rotación es: (Cnb(3,2), Cnb(3,3)), que es el vector formado por los elementos de la tercera fila, segunda columna y tercera columna de la matriz DCM.
6. La fórmula para calcular el ángulo de rotación es: [-asin(-Cnb(3,1)); atan2(Cnb(2,1), Cnb(1,1))], es decir, primero calcula el ángulo de rotación alrededor el eje z (a través de DCM Los signos de los elementos en la fila 3, columna 1 de la matriz están invertidos), y luego calcule el ángulo de rotación alrededor del eje x' (a través de los elementos en la fila 2, columna 1 y fila 1 , columna 1 de la matriz DCM).
7. Almacene el eje de rotación y el ángulo de rotación calculados en la matriz attr, en radianes.
   Cabe señalar que el código utiliza las funciones asin y atan2 en MATLAB para representar las funciones arcoseno y arcocoseno, y juzgar el valor de la variable nargout para determinar la forma del parámetro de salida.

3. Cuaternión -> matriz de actitud: q2mat

$${\mathbf{C}}_b^n=\left[\begin{array}{ccc}{q}_0^2+q_1^2-q_2^2-q_3^2& 2\left(q_1{q}_2-q_0{q}_3\right)& 2\left(q_1{q}_3+q_0{q}_2\right)\\ 2\left(q_1{q}_2+q_0{q}_3\right)& q_0^2-q_1^2+q_2^2-q_3^2& 2\left(q_2{q}_3-q_0{q}_1\right)\\ 2\left(q_1{q}_3-q_0{q}_2\right)& 2\left(q_2{q}_3+q_0{q}_1\right)& q_0^2-q_1^2-q_2^2+q_3^2\end{array}\right]$$

function Cnb = q2mat(qnb)
% Convert attitude quaternion to direction cosine matrix(DCM).
% 四元数 -> 姿态阵
% Prototype: Cnb = q2mat(qnb)
% Input: qnb - attitude quaternion
% Output: Cnb - DCM from body-frame to navigation-frame
    q11 = qnb(1)*qnb(1); q12 = qnb(1)*qnb(2); q13 = qnb(1)*qnb(3); q14 = qnb(1)*qnb(4); 
    q22 = qnb(2)*qnb(2); q23 = qnb(2)*qnb(3); q24 = qnb(2)*qnb(4);     
    q33 = qnb(3)*qnb(3); q34 = qnb(3)*qnb(4);  
    q44 = qnb(4)*qnb(4);
    Cnb = [ q11+q22-q33-q44,  2*(q23-q14),     2*(q24+q13);
            2*(q23+q14),      q11-q22+q33-q44, 2*(q34-q12);
            2*(q24-q13),      2*(q34+q12),     q11-q22-q33+q44 ];

4. 姿态阵 -> 四元数：m2qua

$$\begin{array}{l}{q}_0^{}+q_1^{}-q_2^{}-q_3^{}=C_{}\\ q_0^{}-q_1^{}+q_2^{}-q_3^{}=C_{}\\ q_0^{}-q_1^{}-q_2^{}+q_3^{}=C_{33}\\ q_0^2+q_1^2+q_2^2+q_3^2=1\end{array}\}\Rightarrow \begin{array}{l}\left|q_0\right|=0.5\sqrt{1+C_{11}+C_{22}+C_{33}}\\ \left|q_1\right|=0.5\sqrt{1+C_{11}-C_{22}-C_{33}}\\ \left|q_2\right|=0.5\sqrt{1-C_{11}+C_{22}-C_{33}}\\ \left|q_3\right|=0.5\sqrt{1-C_{11}-C_{22}+C_{33}}\end{array}$$

2 ( q 1 q 2 − q 0 q 3 ) = C 12 2 ( q 1 q 2 + q 0 q 3 ) = C 21 2 ( q 1 q 3 + q 0 q 2 ) = C 13 2 ( q 1 q 3 − q 0 q 2 ) = C 31 2 ( q 2 q 3 − q 0 q 1 ) = C 23 2 ( q 2 q 3 + q 0 q 1 ) = C 32 } ⇒ 4 q 0 q 1 = C 32 − C 23 4 q 0 q 2 = C 13 − C 31 4 q 0 q 3 = C 21 − C 12 4 q 1 q 2 = C 12 + C 21 4 q 1 q 3 = C 13 + C 31 4 q 2 q 3 = C 23 + C 32 } \izquierda.\izquierda.\begin{array}{l}2\left(q_{1} q_{2}-q_{0} q_{3}\right)=C_{12} \\ 2\left(q_{1} q_{2 }+q_{0} q_{3}\right)=C_{21} \\ 2\left(q_{1} q_{3}+q_{0} q_{2}\right)=C_{13} \ \ 2\izquierda(q_{1} q_{3}-q_{0} q_{2}\derecha)=C_{31} \\ 2\izquierda(q_{2} q_{3}-q_{0} q_ {1}\right)=C_{23} \\ 2\left(q_{2} q_{3}+q_{0} q_{1}\right)=C_{32}\end{matriz}\right\ } \Rightarrow \begin{array}{l}4 q_{0} q_{1}=C_{32}-C_{23} \\ 4 q_{0} q_{2}=C_{13}-C_{31 } \\ 4 q_{0} q_{3}=C_{21}-C_{12} \\ 4 q_{1} q_{2}=C_{12}+C_{21} \\ 4 q_{1} q_{3}=C_{13}+C_{31} \\ 4 q_{2} q_{3}=C_{23}+C_{32}\end{matriz}\right\}2( q1q2−q0q3)=C122( q1q2+q0q3)=C212( q1q3+q0q2)=C132( q1q3−q0q2)=C312( q2q3−q0q1)=C232( q2q3+q0q1)=C32​⎭ ⎬ ⎫⇒4q _0q1=C32−C234q _0q2=C13−C314q _0q3=C21−C124q _1q2=C12+C214q _1q3=C13+C314q _2q3=C23+C32​⎭ ⎬ ⎫

Aunque solo sea de acuerdo con la fórmula uno, será difícil determinar los signos positivo y negativo de cada elemento del cuaternión. Si se conoce un determinado elemento del cuaternión, se pueden resolver otros elementos según la fórmula 2, pero se debe evitar que el elemento conocido sea 0. Por condición de normalización de cuaterniones $q_0^{}+q_1^{}$ $+q_2^{}+q_3^{}=1$ muestra que debe haber$\mathrm{máximo}\left(q_i^{}\right)⩾Se\; establece\; 1/4$ , es decir, debe haber algún ∣ qi ∣ ⩾ \left|q_{i}\right| \geqslantentre los cuatro elementos$|q_{}|⩾$ $1/2$ . En la aplicación práctica, un cierto elemento más grande$q_{}$(Se puede tomar como un valor positivo), y luego calcular los tres elementos restantes de acuerdo con la fórmula (B. 10).

function qnb = m2qua(Cnb)
% Convert direction cosine matrix(DCM) to attitude quaternion.
%
% Prototype: qnb = m2qua(Cnb)
% Input: Cnb - DCM from body-frame to navigation-frame
% Output: qnb - attitude quaternion
    C11 = Cnb(1,1); C12 = Cnb(1,2); C13 = Cnb(1,3); 
    C21 = Cnb(2,1); C22 = Cnb(2,2); C23 = Cnb(2,3); 
    C31 = Cnb(3,1); C32 = Cnb(3,2); C33 = Cnb(3,3); 
%     q0t = 0.5*sqrt(1+C11+C22+C33);
%     q1t = 0.5*sqrt(1+C11-C22-C33);
%     q2t = 0.5*sqrt(1-C11+C22-C33);
%     q3t = 0.5*sqrt(1-C11-C22+C33);
    if C11>=C22+C33
        q1 = 0.5*sqrt(1+C11-C22-C33);  qq4 = 4*q1;
        q0 = (C32-C23)/qq4; q2 = (C12+C21)/qq4; q3 = (C13+C31)/qq4;
    elseif C22>=C11+C33
        q2 = 0.5*sqrt(1-C11+C22-C33);  qq4 = 4*q2;
        q0 = (C13-C31)/qq4; q1 = (C12+C21)/qq4; q3 = (C23+C32)/qq4;
    elseif C33>=C11+C22
        q3 = 0.5*sqrt(1-C11-C22+C33);  qq4 = 4*q3;
        q0 = (C21-C12)/qq4; q1 = (C13+C31)/qq4; q2 = (C23+C32)/qq4;
    else
        q0 = 0.5*sqrt(1+C11+C22+C33);  qq4 = 4*q0;
        q1 = (C32-C23)/qq4; q2 = (C13-C31)/qq4; q3 = (C21-C12)/qq4;
    end
    qnb = [q0; q1; q2; q3];

Explicación de AI :
la función acepta un parámetro de entrada Cnb, que es una matriz de 3x3 que representa el DCM desde el sistema de coordenadas del cuerpo hasta el sistema de coordenadas de navegación. La salida de la función es un vector cuaternión qnb que representa la actitud correspondiente para un DCM dado. La implementación del código es la siguiente:

1. Extraiga los valores de los elementos de la matriz Cnb de entrada y asígnelos a las variables C11, C12, C13, C21, C22, C23, C31, C32 y C33 respectivamente.
2. En función de los valores de los elementos del DCM, se utilizan una serie de declaraciones condicionales para determinar cómo se calcula cada elemento y luego se calculan los elementos individuales del vector cuaternión.
3. De acuerdo con el resultado del juicio condicional, seleccione un método de cálculo apropiado para obtener el vector cuaternión final qnb.

5. Ángulo de Euler -> cuaternión: a2qua

Los cuaterniones se usan comúnmente en algoritmos de actualización de actitud de navegación inercial. Los resultados de salida de la navegación inercial a menudo se expresan como ángulos de Euler, y se requiere una conversión mutua entre cuaterniones y ángulos de Euler. De acuerdo con el significado geométrico de los cuaterniones unitarios:
$$\begin{array}{rl}{q}_b^{}=& q_{}\circ Q_{}\circ q_{}=\left({do}_{\psi /}+k{s}_{\psi /}\right)\circ \left({do}_{\theta /}+yo{s}_{\theta /}\right)\circ \left({do}_{c/}+js{\_}_{c/}\right)=\\ & \left({do}_{\psi /}{C}_{\theta /}+yo{c}_{\psi /}{s}_{\theta /}+k{s}_{\psi /}{C}_{\theta /}+k\circ i_{\psi /}{s}_{\theta /}\right)\circ \left({do}_{c/}+js{\_}_{c/}\right)=\\ & \left({do}_{\psi /}{C}_{\theta /}+yo{c}_{\psi /}{s}_{\theta /}+k{s}_{\psi /}{C}_{\theta /}+js{\_}_{\psi /}{s}_{\theta /}\right)\circ \left({do}_{c/}+js{\_}_{c/}\right)=\\ & \left[\begin{array}{l}{C}_{\psi /}{C}_{\theta /}{C}_{c/}-s_{\psi /}{s}_{\theta /}{s}_{c/}\\ C_{\psi /}{s}_{\theta /}{C}_{c/}-s_{\psi /}{C}_{\theta /}{s}_{c/}\\ s_{\psi /}{s}_{\theta /}{C}_{c/}+C_{\psi /}{C}_{\theta /}{s}_{c/}\\ s_{\psi /}{C}_{\theta /}{C}_{c/}+C_{\psi /}{s}_{\theta /}{s}_{c/}\end{array}\right]\end{array}$$

function qnb = a2qua(att)
% Convert Euler angles to attitude quaternion.
% 欧拉角 -> 四元数
% Prototype: qnb = a2qua(att)
% Input: att - att=[pitch; roll; yaw] in radians
% Output: qnb - attitude quaternion
    att2 = att/2;
    s = sin(att2); c = cos(att2);
    sp = s(1); sr = s(2); sy = s(3); 
    cp = c(1); cr = c(2); cy = c(3); 
    qnb = [ cp*cr*cy - sp*sr*sy;
            sp*cr*cy - cp*sr*sy;
            cp*sr*cy + sp*cr*sy;
            cp*cr*sy + sp*sr*cy ];

Explicación de AI :
la salida del número es un cuaternión qnb, que representa la actitud correspondiente al ángulo de Euler dado. La implementación del código es la siguiente:

1. Divide el vector att por 2 para obtener el vector att2, que representa la mitad de cada ángulo.
2. Utilice las funciones sin y cos para calcular los valores de seno y coseno del vector att2 para obtener los vectores s y c correspondientes.
3. Asigne los elementos de los vectores s y c a las variables sp, sr, sy, cp, cr y cy, respectivamente, para cálculos posteriores.
4. Calcula cada elemento del cuaternión qnb según la fórmula del cuaternión.

6. Cuaternión -> Ángulo de Euler: q2att

No es fácil resolver directamente el ángulo de Euler por cuaternión, y la matriz de actitud se puede usar como una cantidad de transición intermedia.
$$\begin{array}{l}i=\mathrm{arcsen}\left(2\left(q_{}{q}_{}+q_{}{q}_{}\right)\right)\\ \left\{\begin{array}{ll}C=-con\; el\; propósito2\left(2\left(q_{}{q}_{}-q_{}{q}_{}\right),q_0^{}-q_1^{}-q_2^{}+q_3^{}\right)& \\ pag=-con\; el\; propósito2(2\left(q_{}{q}_{}-q_{}{q}_{}\right),q_0^{}-q_1^{}+q_2^{}-q_3^{}& |2\left(q_{}{q}_{}+q_{}{q}_{}\right)|⩽\end{array}\right\}\\ \{\begin{array}{ll}C=con\; el\; propósito2\left(2\left(q_{}{q}_{}+q_{}{q}_{}\right),q_0^{}+q_1^{}-q_2^{}-q_3^{}\right)& |2\left(q_{}{q}_{}+q_{}{q}_{}\right)|>0.999999\\ pag=& \end{array}\end{array}$$

function att = q2att(qnb)
% Convert attitude quaternion to Euler attitude angles.
% 四元数 -> 欧拉角
% Prototype: att = q2att(qnb)
% Input: qnb - attitude quaternion
% Output: att - Euler angles att=[pitch; roll; yaw] in radians
    q11 = qnb(1)*qnb(1); q12 = qnb(1)*qnb(2); q13 = qnb(1)*qnb(3); q14 = qnb(1)*qnb(4); 
    q22 = qnb(2)*qnb(2); q23 = qnb(2)*qnb(3); q24 = qnb(2)*qnb(4);     
    q33 = qnb(3)*qnb(3); q34 = qnb(3)*qnb(4);  
    q44 = qnb(4)*qnb(4);
    C12=2*(q23-q14);
    C22=q11-q22+q33-q44;
    C31=2*(q24-q13); C32=2*(q34+q12); C33=q11-q22-q33+q44;
    att = [ asin(C32); 
            atan2(-C31,C33); 
            atan2(-C12,C22) ];

Explicación de AI :
este código es una función que convierte cuaterniones en ángulos de Euler. Toma un cuaternión como entrada y devuelve un vector que contiene los ángulos de Euler (cabeceo, guiñada y balanceo). Los pasos principales del código son los siguientes:

1. Definición de variables: primero, el código descompone el cuaternión de entrada en los cuadrados de sus componentes y los almacena en las variables q11, q22, q33 y q44. Estas variables se utilizan en cálculos posteriores.
2. Definición de los elementos de la matriz de rotación: A continuación, el código utiliza los componentes del cuaternión para calcular los elementos C12, C22, C31, C32 y C33 de la matriz de rotación. Estos elementos se utilizarán para calcular los ángulos de Euler.
3. Calcular ángulos de Euler: Finalmente, el código usa los elementos de la matriz de rotación para calcular los ángulos de Euler. Primero, use la función asen para calcular el valor de C32 para obtener el ángulo de inclinación. Luego, use la función atan2 para calcular la tangente de los valores de C31 y C33 para obtener el ángulo de guiñada. Finalmente, utilice la función atan2 para calcular la tangente de los valores de C12 y C22 para obtener el ángulo de balanceo.
4. Finalmente, la función devuelve un vector att que contiene los ángulos de Euler (cabeceo, guiñada y balanceo). Estos ángulos de Euler representan el ángulo de rotación de la pose correspondiente al cuaternión en el espacio tridimensional.

7. Cuaternión -> Vector de rotación equivalente: q2rv

function rv = q2rv(q) 
% Convert transformation quaternion to rotation vector.
%  四元数 -> 等效旋转矢量
% Prototype: rv = q2rv(q) 
% Input: q - transformation quaternion
% Output: rv - corresponding rotation vector, such that
	if(q(1)<0)
	    q = -q;
	end
    n2 = acos(q(1));
    if n2>1e-40
        k = 2*n2/sin(n2);
    else
        k = 2;
    end
    rv = k*q(2:4);   % q = [ cos(|rv|/2); sin(|rv|/2)/|rv|*rv ];

Explicación de AI :
este código es una función que convierte un cuaternión transformado en un vector de rotación equivalente. Toma un cuaternión como entrada y devuelve el vector de rotación correspondiente. Los pasos principales del código son los siguientes:

1. Conversión del signo del cuaternión: el código primero comprueba si el primer elemento del cuaternión es negativo. Si es negativo, el cuaternión se niega para garantizar que el signo del vector de rotación sea el esperado.
2. Calcular la magnitud del vector de rotación: el código usa la función acos para calcular el arcocoseno del primer elemento del cuaternión para obtener la magnitud del vector de rotación (también conocido como ángulo de rotación). Aquí se usa una declaración condicional, si n2 (es decir, el ángulo de rotación) es mayor que un pequeño umbral (1e-40), el tamaño del vector de rotación se calcula mediante una fórmula; de lo contrario, el tamaño del vector de rotación es establecido en 2.
3. Calcular la dirección del vector de rotación: De acuerdo con la magnitud del vector de rotación, el código utiliza las funciones seno y coseno para calcular la dirección del vector de rotación correspondiente a los elementos segundo a cuarto del cuaternión. Específicamente, la dirección del vector de rotación se obtiene multiplicando la magnitud del vector de rotación por el producto del segundo al cuarto elemento del cuaternión.
4. Finalmente, la función devuelve el vector de rotación calculado rv. Este vector de rotación representa el vector de rotación equivalente de la actitud correspondiente al cuaternión en el espacio tridimensional.

Tenga en cuenta que durante la conversión, el signo del código ajusta el cuaternión de entrada para garantizar que el signo del vector de rotación sea el esperado.

8. Vector de rotación equivalente -> cuaternión: rv2q

Primero, convierta el cuaternión en un cuaternión escalar no negativo; segundo, según la fórmula $q=q_{}+q_{}=\mathrm{porque}\frac{}{2}+tu\mathrm{pecado}\frac{}{2}=$ $\mathrm{porque}\frac{}{2}+\frac{}{2}\cdot \frac{syonorte(\varphi /\; 2}{/2}$, primero de la relación escalar del cuaternión $q_{}=\mathrm{porque}\frac{}{2}$Encuentra la mitad del módulo del vector de rotación $\frac{}{2}=$ $\arccos \left(q_{}\right)$ , y luego por la relación vectorial$q_{}=\frac{}{2}\cdot \frac{syonorte(\varphi /\; 2}{/2}$Encuentra el vector de rotación equivalente $\varphi =2\frac{(\varphi /2}{syonorte(\varphi /\; 2)}{q}_{}$Q = q 0 + qv = porque ⁡ ϕ 2 + tu sin ⁡ ϕ 2 Q=q_{0} +
$$q=q_{}+q_{}=\mathrm{porque}\frac{}{2}+tu\mathrm{pecado}\frac{}{2}$$

function q = rv2q(rv)
% Convert rotation vector to transformation quaternion.
%
% Prototype: q = rv2q(rv)
% Input: rv - rotation vector
% Output: q - corresponding transformation quaternion, such that
%             q = [ cos(|rv|/2); sin(|rv|/2)/|rv|*rv ]
    q = zeros(4,1);
    n2 = rv(1)*rv(1) + rv(2)*rv(2) + rv(3)*rv(3);
    if n2<1.0e-8  % cos(n/2)=1-n2/8+n4/384; sin(n/2)/n=1/2-n2/48+n4/3840
        q(1) = 1-n2*(1/8-n2/384); s = 1/2-n2*(1/48-n2/3840);
    else
        n = sqrt(n2); n_2 = n/2;
        q(1) = cos(n_2); s = sin(n_2)/n;
    end
    q(2) = s*rv(1); q(3) = s*rv(2); q(4) = s*rv(3);

Este código es una función que convierte un vector de rotación en un cuaternión de transformación. Toma un vector de rotación como entrada y devuelve el cuaternión de transformación correspondiente. Los pasos principales del código son los siguientes:

1. Inicialice el cuaternión: el código primero crea un vector cero q de tamaño 4, que se utiliza para almacenar los elementos del cuaternión transformado.
2. Calcular la magnitud del vector de rotación: el código utiliza el primer elemento del vector de rotación como la magnitud del vector de rotación (también conocido como ángulo de rotación). Aquí se usa una declaración condicional. Si el cuadrado estándar del vector de rotación es menor que un umbral pequeño (1.0e-8), el tamaño del vector de rotación se calcula usando la expansión de la serie de Taylor; de lo contrario, el tamaño del vector de rotación es calculado por la fórmula estándar.
3. Calcular la dirección del vector de rotación: en función de la magnitud del vector de rotación, el código utiliza las funciones seno y coseno para calcular la dirección del vector de rotación. Específicamente, la dirección del vector de rotación se obtiene multiplicando la magnitud del vector de rotación por el signo del primer elemento del vector de rotación y multiplicando el resultado por los otros tres elementos del vector de rotación.
4. Construir cuaternión de transformación: según el tamaño y la dirección del vector de rotación, el código construye el cuaternión de transformación correspondiente. Específicamente, divida la magnitud del vector de rotación por 2, luego use las funciones seno y coseno para calcular los elementos individuales del cuaternión transformado.
5. Finalmente, la función devuelve el cuaternión de transformación calculado q. Este cuaternión de transformación representa la representación de la pose correspondiente al vector de rotación en el espacio del cuaternión.

Tenga en cuenta que en el proceso de cálculo, el código usa diferentes fórmulas para tratar con diferentes situaciones del tamaño del vector de rotación para mejorar la precisión del cálculo.

9. Matriz de actitud -> Vector de rotación equivalente: m2rv

function rv = m2rv(m)
% Convert transformation matrix to rotation vector.
%
% Prototype: rv = m2rv(m)
% Input: m - transformation matrix
% Output: rv - corresponding rotation vector, such that
        rv = [m(3,2)-m(2,3); m(1,3)-m(3,1); m(2,1)-m(1,2)];  % 11/10/2022
        phi = acos((m(1,1)+m(2,2)+m(3,3)-1)/2);
        if phi<1e-10, afa=1/2; else afa=phi/(2*sin(phi)); end
%         afa = phi/sqrt(rv'*rv);
        rv = afa*rv;
        return;
%     rv = iaskew(m-glv.I33);  % coarse init is ok when rv is small, otherwise may fail
%     rvx = askew(rv); % good! the following iteration due to the
    for k=1:2        % accuracy deduce of sqrt(.) in function m2qua
        xx = rv(1)*rv(1); xy = rv(1)*rv(2); xz = rv(1)*rv(3);
        yy = rv(2)*rv(2); yz = rv(2)*rv(3); zz = rv(3)*rv(3);
        n2 = xx+yy+zz;
%         n2 = rv'*rv; 
        if n2>1.0e-40
            n = sqrt(n2);
%             rvx = (m-eye(3)-(1-cos(n))/n2*rvx*rvx) * (n/sin(n));
            rvx = (m1-(1-cos(n))/n2*[-yy-zz,xy,xz; xy,-xx-zz,yz; xz,yz,-xx-yy]) * (n/sin(n));
            rv = [rvx(3,2); rvx(1,3); rvx(2,1)]; % rv = iaskew(rvx);
        else
            rv = zeros(3,1);
            break;
        end
    end

Explicación de AI:
este código es una función que convierte una matriz de transformación en un vector de rotación. Sus principales funciones son las siguientes:

1. Calcule el vector de rotación: al restar los elementos en la diagonal de los elementos de la matriz de transformación y luego aplicar un cierto paso de cálculo, se obtiene el vector de rotación.
2. Calcule el ángulo de rotación: use la función acos para calcular el ángulo de rotación en el vector de rotación.
3. Calcular el coeficiente de normalización del vector de rotación: Calcular el coeficiente de normalización del vector de rotación según el valor del ángulo de rotación. Si el ángulo de rotación es muy pequeño (menos de 1e-10), establezca el factor de normalización en 1/2; de lo contrario, calcule según la fórmula.
4. Normalizar vector de rotación: normaliza el vector de rotación utilizando un factor de normalización.
5. Calcule iterativamente el vector de rotación: calcule iterativamente el vector de rotación a través de un bucle. Primero, inicialice el vector de rotación a un vector con una pequeña diferencia de la matriz de transformación (usando inicio grueso). Luego, el vector de rotación se actualiza a través de una serie de pasos computacionales. Este proceso iterativo se realiza dos veces.

10. Vector de rotación equivalente -> matriz de actitud: rv2m

$$C_b^{}=I+\frac{\mathrm{pecado}}{\varphi }(\varphi \times )+\frac{1-\mathrm{porque}}{{\varphi }^2}(\varphi \times {)}^2$$

function m = rv2m(rv)
% Convert rotation vector to transformation matrix.
% 等效旋转矢量 -> 姿态阵
% Prototype: m = rv2m(rv)
% Input: rv - rotation vector
% Output: m - corresponding DCM, such that

	xx = rv(1)*rv(1); yy = rv(2)*rv(2); zz = rv(3)*rv(3);
	n2 = xx+yy+zz;
    if n2<1.e-8
        a = 1-n2*(1/6-n2/120); b = 0.5-n2*(1/24-n2/720);  % a->1, b->0.5
    else
        n = sqrt(n2);
        a = sin(n)/n;  b = (1-cos(n))/n2;
    end
	arvx = a*rv(1);  arvy = a*rv(2);  arvz = a*rv(3);
	bxx = b*xx;  bxy = b*rv(1)*rv(2);  bxz = b*rv(1)*rv(3);
	byy = b*yy;  byz = b*rv(2)*rv(3);  bzz = b*zz;
	m = zeros(3,3);
	% m = I + a*(rvx) + b*(rvx)^2;
	m(1)=1     -byy-bzz; m(4)= -arvz+bxy;     m(7)=  arvy+bxz;
	m(2)=  arvz+bxy;     m(5)=1     -bxx-bzz; m(8)= -arvx+byz;
	m(3)= -arvy+bxz;     m(6)=  arvx+byz;     m(9)=1     -bxx-byy;

Explicación de AI:
esta función es una función que convierte un vector de rotación en una matriz de pose. Toma un vector de rotación como entrada y devuelve la matriz de pose correspondiente como salida. El proceso es el siguiente:

1. Primero, la función calcula los tres componentes del vector de rotación (es decir, xx, yy y zz) tomando el producto escalar del vector de rotación de entrada y el vector unitario, respectivamente.
2. A continuación, la función calcula una variable n2 que es igual a la suma de los cuadrados de las tres componentes del vector de rotación. Si n2 es menor que un umbral pequeño (1.e-8), entonces la longitud del vector de rotación es muy cercana a cero, en cuyo caso se utiliza una solución aproximada para calcular los elementos de la matriz de pose.
3. Si n2 es mayor o igual a 1.e-8, significa que la longitud del vector de rotación no es 0. En este momento, se utiliza la expansión de la serie de Taylor para calcular los elementos de la matriz de actitud. En este caso, la función primero calcula la longitud n del vector de rotación y luego calcula los valores de sin(n) y (1-cos(n)) según la longitud n, que se utilizará para construir el elementos de la matriz de pose.
4. A continuación, la función construye cada elemento de la matriz de pose en función de los valores calculados anteriormente. Estos elementos incluyen a rv(1), a rv(2) y a rv(3), y b xx, b rv(1) rv(2), b rv(1) rv(3), b yy, b rv(2) rv(3) y bzz .
5. Finalmente, la función llena estos elementos en una matriz de 3x3 y devuelve esta matriz como salida.

En resumen, la función de esta función es convertir el vector de rotación en una matriz de pose. Utiliza la expansión de la serie de Taylor y soluciones aproximadas para manejar el caso en el que la longitud del vector de rotación es cercana a cero para evitar inestabilidades numéricas.

11. Matriz antisimétrica

askew: Encuentre la matriz antisimétrica del vector tridimensional

function m = askew(v)
    m = [ 0,     -v(3),   v(2); 
          v(3),   0,     -v(1); 
         -v(2),   v(1),   0     ];