

La analogía es una de nuestras formas de pensar más antiguas y juega un papel importante en inspirar a los seres humanos a hacer nuevos descubrimientos. A menudo pensamos que estamos familiarizados con el razonamiento analógico, pero a veces nos negamos a aceptar conclusiones analógicas obvias debido a nuestras propias limitaciones cognitivas.
Los seres humanos han estado mirando a la luna desde la antigüedad. Durante mucho tiempo se creyó que la luna era perfecta y el dominio de los dioses, si se rompía el equilibrio del halo de la luna y ocurría un eclipse lunar, los humanos tendríamos que usar varias acciones para corregirlo: los chinos arrojaban espejos, los incas gritaban y los romanos agitaban antorchas frenéticamente. No fue hasta que Galileo apuntó su telescopio a la luna en 1609 que descubrió que no era lisa ni perfecta, sino un revoltijo de acantilados y cráteres.
Galileo, como algunos otros astrónomos, vio en un telescopio que había puntos de luz en la parte oscura de la luna, que gradualmente se hicieron más grandes y brillantes, y finalmente se fusionaron con otras partes brillantes. Galileo sintió que este fenómeno es muy similar al sol de la mañana que brilla en una montaña. Cuanto más alto sube el sol, más pequeña se encoge la sombra del valle, y finalmente toda la montaña es bañada por la luz del sol. Creía que las sombras y otros fenómenos ópticos deberían ser iguales en la Tierra y en la Luna. Por tanto, Galileo concluyó que la superficie de la luna no debe ser lisa, sino alta y baja, como la tierra, con montañas y valles.
Este es el poder de la analogía.
Entonces, ¿qué es una analogía?
Una analogía compara dos cosas, destacando aspectos de ellas que se consideran similares, y su objetivo principal es explicar algo que no nos es familiar en términos de algo con lo que estamos familiarizados. El razonamiento por analogía es una forma de pensar basada en la analogía. Deduce que otro atributo de dos (o dos tipos) cosas es igual o similar basado en los mismos o similares atributos. Es un proceso de razonamiento especial a especial.
Una historia sobre Zou Ji está registrada en el famoso libro chino antiguo "Política de los Estados Combatientes", que puede considerarse como un excelente caso de razonamiento analógico.
Zou Ji tiene más de ocho pies, pero su apariencia es hermosa. Vestido con ropa de corte y mirándose en el espejo, le dijo a su esposa: "¿Quién soy tan hermoso como Xu Gong en el norte de la ciudad?" Su esposa dijo: "El rey es tan hermoso, ¿cómo puede Xu Gong ser tan bueno como el rey?" Evite no tener confianza, pero pregúntele a su concubina nuevamente: "¿Cuál es más hermoso que el Sr. Xu?" La concubina dijo: "¿Cómo puede el Sr. Xu ser tan bueno como el rey?" Cuando me acuesto por la noche, pienso en ello y digo: "Mi esposa, que es hermosa para mí, es egoísta; la concubina, que es hermosa para mí, me tiene miedo; el huésped que es hermoso para mí, pregunta por mí".
Entonces fue a la corte para encontrarse con el rey Wei y dijo: "Sé que no soy tan hermoso como Xu Gong. La esposa del ministro es privada, la concubina del ministro le tiene miedo al ministro y el invitado del ministro quiere preguntarle al ministro. Todos son más hermosos que Xu Gong. Hoy en día, hay miles de millas en Qi y hay cientos de ciudades. No hay damas de la corte que sean privadas del rey, y todos los funcionarios de la corte no le temen al rey, y no hay nadie en el cuatro reinos que no busca al rey. Desde este punto de vista, el rey está muy escondido".
En la historia anterior, Zou Ji analizó las razones por las que sus esposas, concubinas e invitados no le dijeron la verdad, y aplicó este conjunto de razonamientos a escenas similares (es decir, la relación entre el rey Qiwei y las damas de la corte, los cortesanos y otros estados vasallos), y llegó a la conclusión de que "la ocultación del rey es demasiado", lo que finalmente hizo que el rey Qiwei aceptara vigorosamente los consejos y lograra grandes logros.
En la historia anterior de Galileo, basada en un hecho (la sombra y los fenómenos ópticos no cambian debido a la tierra y la luna) y fenómenos de observación similares, Galileo especuló que la luna debería tener la misma montaña y el mismo valle que la tierra.
El razonamiento por analogía es la base del pensamiento humano y, posiblemente, también de algunos animales no humanos. Desde la perspectiva de la historia del desarrollo humano, como medio auxiliar para generar nuevos descubrimientos, se cree ampliamente que la analogía juega un papel heurístico importante. El pionero de la química, Joseph Priestley, creía que la analogía era la mejor guía para toda investigación, con la ayuda de la cual se hacían todos los descubrimientos no accidentales.
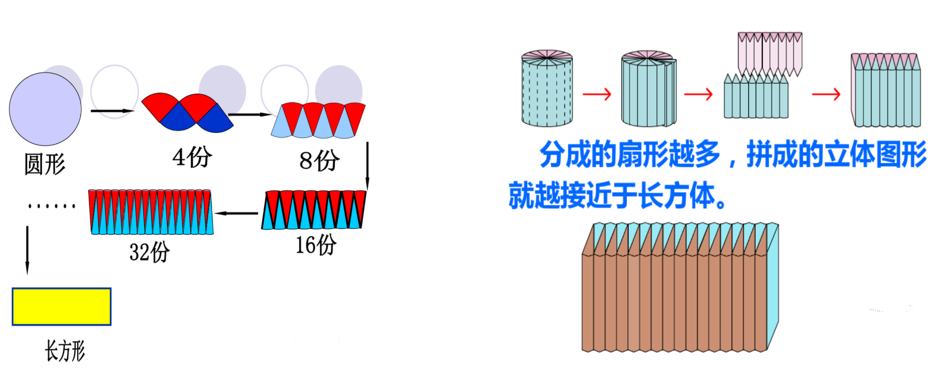
En los libros de texto de matemáticas de la escuela primaria, hay un buen caso de analogía, es decir, la analogía entre el método de derivación del área de un círculo y el método de derivación de un cilindro. Al derivar el área de un círculo, el círculo se corta en muchos sectores pequeños y finalmente se ensambla en un rectángulo aproximado. De manera similar, al derivar el volumen de un cilindro, el cilindro se corta en cilindros pequeños y finalmente se ensambla en un paralelepípedo aproximado.
A partir del objeto de la analogía, la analogía se puede dividir en: analogía de concepto y operación, analogía de conclusión, analogía de método.
Un ejemplo clásico de una analogía conceptual es la definición de un círculo y una esfera. Sabemos que la definición de un círculo es un conjunto (una curva) de todos los puntos con distancias iguales desde el centro del círculo, entonces la definición de una esfera en tres dimensiones debe ser un conjunto de puntos con distancias iguales desde el centro de la esfera (una superficie curva).
A través de la analogía, a menudo podemos descubrir algunas conclusiones nuevas.
Por ejemplo, supongamos que conocemos la siguiente proposición: De todos los rectángulos con un perímetro fijo, un cuadrado tiene el área más grande.
¿Se puede extender esta conclusión al espacio tridimensional por analogía? Para ello, primero tenemos que hacer una analogía entre los conceptos bidimensionales y tridimensionales involucrados en esta proposición, como se muestra en la siguiente tabla.
El concepto de espacio bidimensional. |
El concepto de espacio tridimensional. |
rectángulo |
cuboides |
cuadrado |
Cubo |
perímetro |
área de superficie |
área |
volumen |
De esto, ¿podemos deducir la conclusión de la analogía tridimensional de la proposición anterior: entre todos los cuboides con área de superficie fija, el cubo tiene el volumen más grande?
A continuación, daré algunos casos típicos de razonamiento por analogía.
Analogía de no decimal a decimal
Sabemos que en el sistema decimal, la característica de un número divisible por 9 es que la suma de sus dígitos puede ser divisible por 9. El proceso de razonamiento se basa en la representación del valor en bits del número, por ejemplo:
297=2×10 2 +9×10+7
=2×(99+1)+9×(9+1)+7
=2×99+9×9+2+9+7
Por lo tanto, 297 es divisible por 9 si y solo si la suma de sus dígitos, 2+9+7, es divisible por 9.
Entonces, ¿podemos extender esta conclusión y proceso de razonamiento a otros sistemas? Por ejemplo, en base 7, ¿qué conclusiones podemos sacar?
Aquí, 9 en decimal debería corresponder a 6 en base 7. Por lo tanto, podemos proponer audazmente la siguiente conclusión de analogía: En base 7, la característica de un número divisible por 6 es que la suma de los dígitos puede ser divisible por 6.
Si esta conclusión es correcta o no, también podemos verificarla por analogía con el proceso de razonamiento decimal.
435 (7) =4×100 (7) +3×10 (7) +5
=4×(66 (7) +1)+3×(6 (7) +1)+5
=4×66 (7) +3×6 (7) +4+3+5
Por tanto, 435 (7) es divisible por 6, lo que equivale a que 4+3+5 sea divisible por 6.
También sabemos que las fracciones decimales cíclicas decimales tienen las siguientes conclusiones:
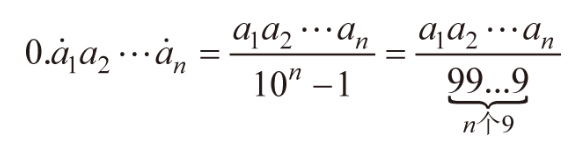
Si no se utiliza la suma de series infinitas, el proceso de derivación es el siguiente:
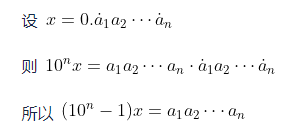
Para otras bases, como la base 7, se pueden sacar conclusiones similares por analogía:
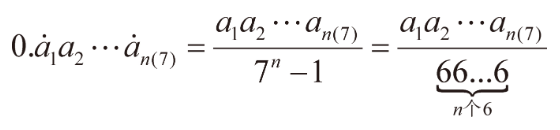
Su método de razonamiento también se puede comparar con el razonamiento decimal:
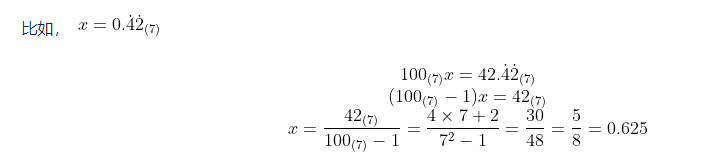
principio ancestral
El principio de Zuo es una proposición bien conocida que involucra la cuadratura geométrica. Dice esto: si el potencial de potencia es el mismo, el producto no puede ser diferente. "Potencia" es el área de la sección transversal, y "potencial" es la altura del sólido. Significa que si dos sólidos delimitados entre dos planos paralelos son cortados por cualquier plano paralelo a estos dos planos, si las áreas de las dos secciones transversales son iguales, entonces los volúmenes de los dos sólidos son iguales.

Si este principio se aplica a un plano bidimensional, ¿qué conclusiones se pueden sacar?
Para ello, primero tenemos que hacer una analogía conceptual entre 3D y 2D:
Conceptos en 3D |
Conceptos en 2D |
tridimensional |
Gráficos |
volumen |
área |
sección |
segmento de intercepción |
alto |
alto |
plano paralelo |
lineas paralelas |
departamento |
línea recta |
área |
longitud |
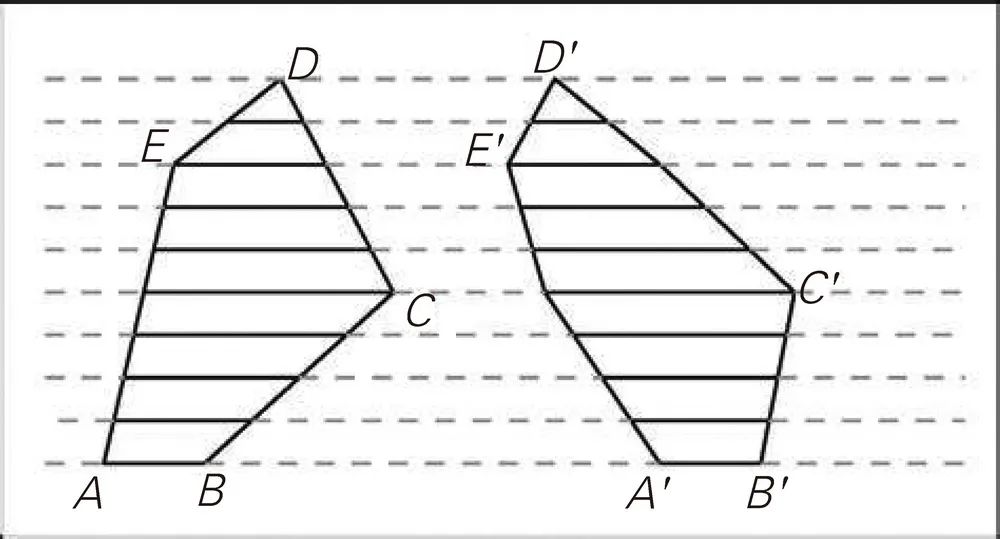
A partir de esto, podemos obtener la conclusión de analogía bidimensional del principio de Zuo: si dos figuras planas delimitadas por dos líneas paralelas son cortadas por cualquier línea recta paralela a estas dos líneas paralelas, si las longitudes de las dos secciones de las líneas cortadas son iguales, entonces las áreas de las dos figuras planas son iguales.
Centro de gravedad de triángulos y tetraedros
Podemos encontrar el centro de gravedad del triángulo de la siguiente manera: las tres líneas medias del triángulo se cruzan en un punto, que es el centro de gravedad del triángulo (punto G como se muestra en la figura a continuación).
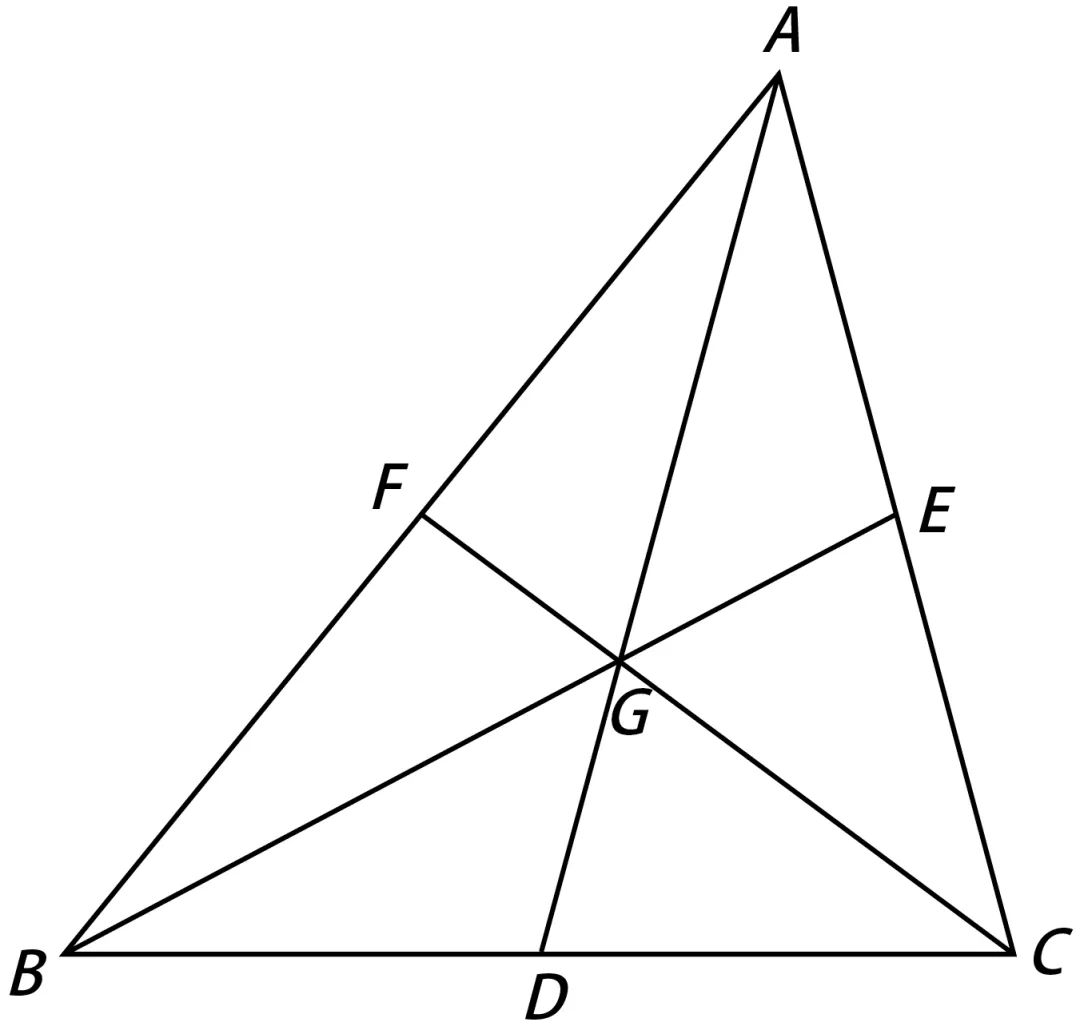
Para un tetraedro, ¿es posible encontrar su centro de gravedad de manera similar?
Para esto, también necesitamos involucrar analogías conceptuales.
Conceptos en 2D |
Conceptos en 3D |
triángulo |
tetraedro |
línea media |
cara media |
punto de intersección de la línea recta |
intersección de plano a plano |
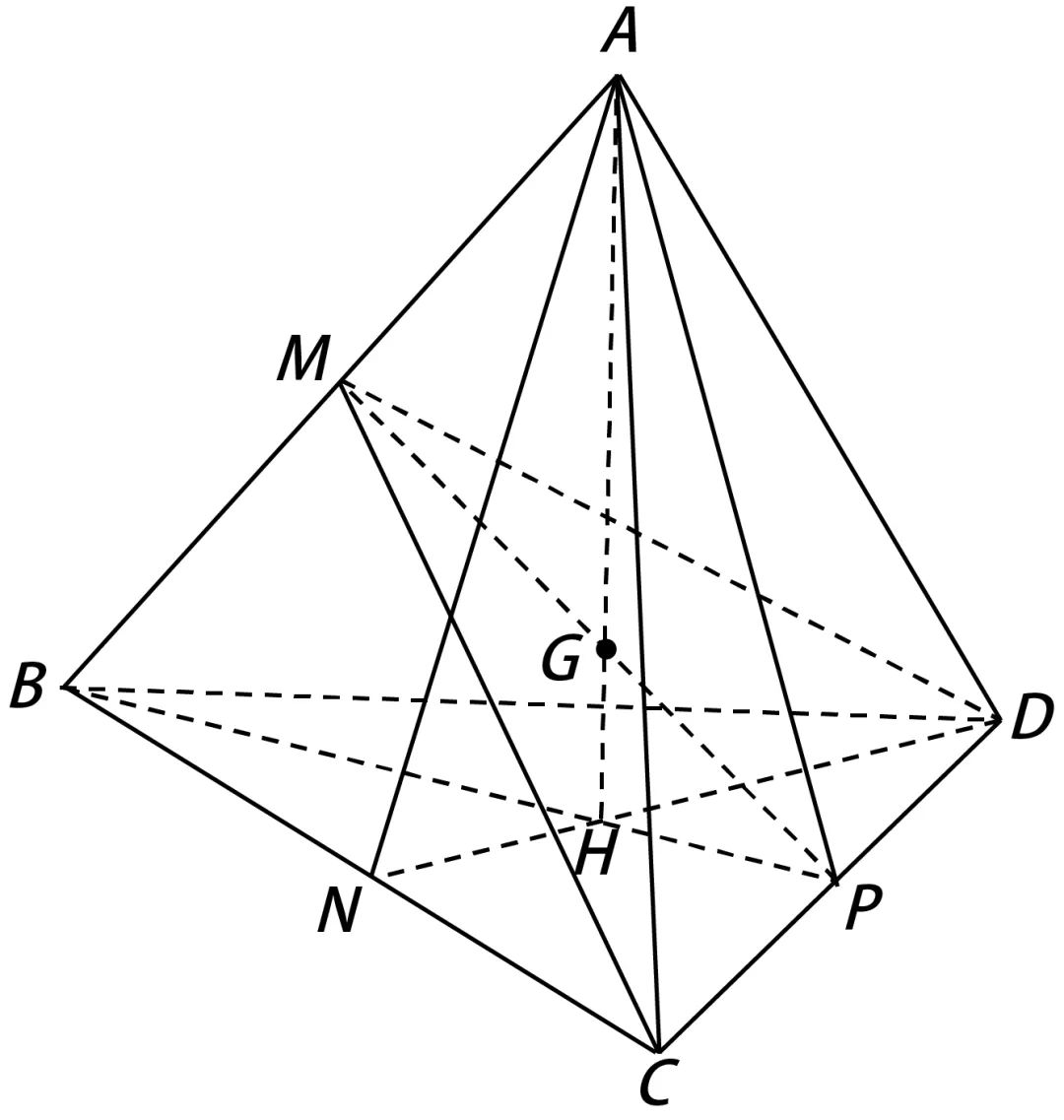
Con base en esto, podemos hacer una analogía: el triángulo que conecta una arista de un tetraedro con el punto medio de la arista opuesta se llama plano medio del tetraedro, luego hay 6 planos medios en total, y estos 6 planos medios se cruzan en un punto, que es el centro de gravedad del tetraedro.
Aunque ahora no estamos probando la conclusión de si los seis planos medios se intersecan en un punto, al menos tenemos la corazonada de que la conclusión extraída de esta analogía debería ser correcta.
Cálculo Encontrar área y volumen
Al calcular el área del cálculo, consideramos una figura plana como una figura compuesta por innumerables rectángulos pequeños. (Nota: no se deje intimidar por el nombre de cálculo. De hecho, los estudiantes de escuela primaria generalmente pueden entender los principios del cálculo. El área de un círculo se calcula usando cálculo).
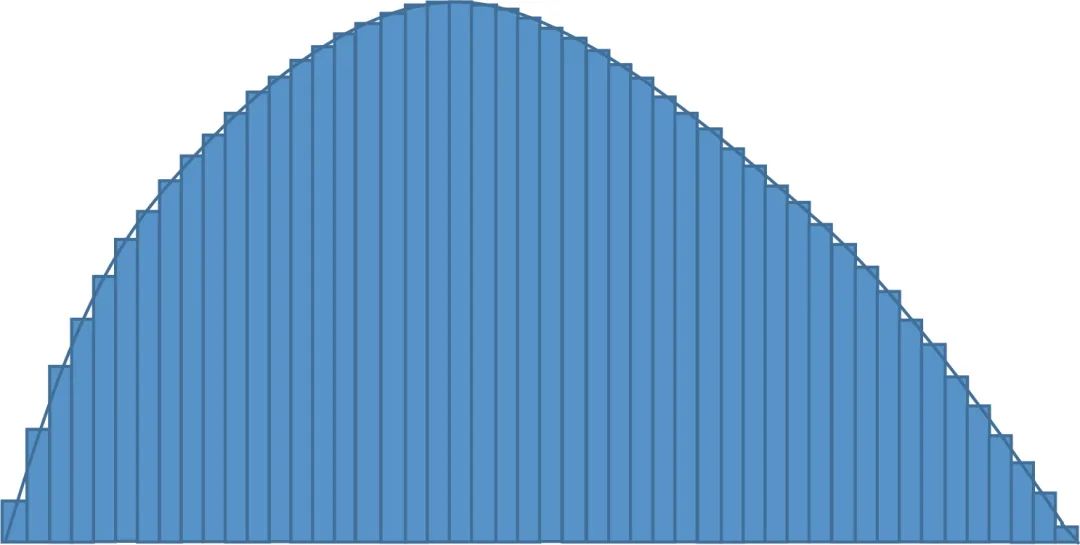
Por analogía, podemos aplicar este método para encontrar el volumen de un objeto en un espacio tridimensional. En este momento, consideramos la figura tridimensional como una figura compuesta de infinitos cilindros. Aquí, un rectángulo en dos dimensiones es análogo a un cilindro en tres dimensiones.
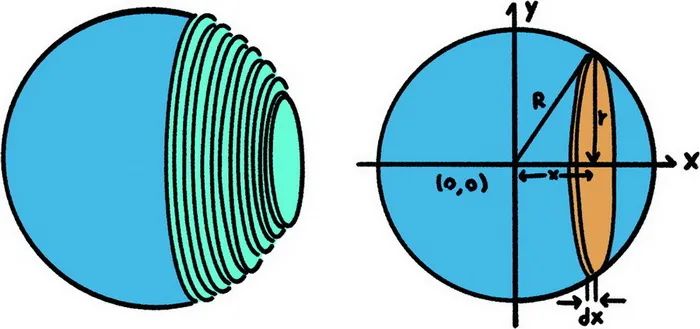
división infinita
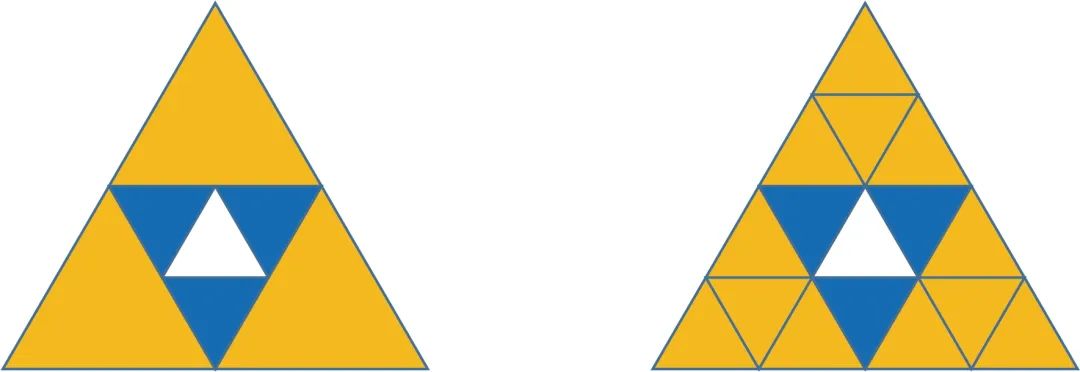
El cuadrado de la siguiente figura tiene una longitud de lado de 1. Primero, se divide en cuatro cuadrados iguales y se colorea la esquina superior izquierda. Luego, el cuadrado de la esquina inferior derecha se divide en cuatro y se colorea la esquina superior izquierda. Si continuamos con este proceso, ¿cuánto del área total es la última parte que se pinta?
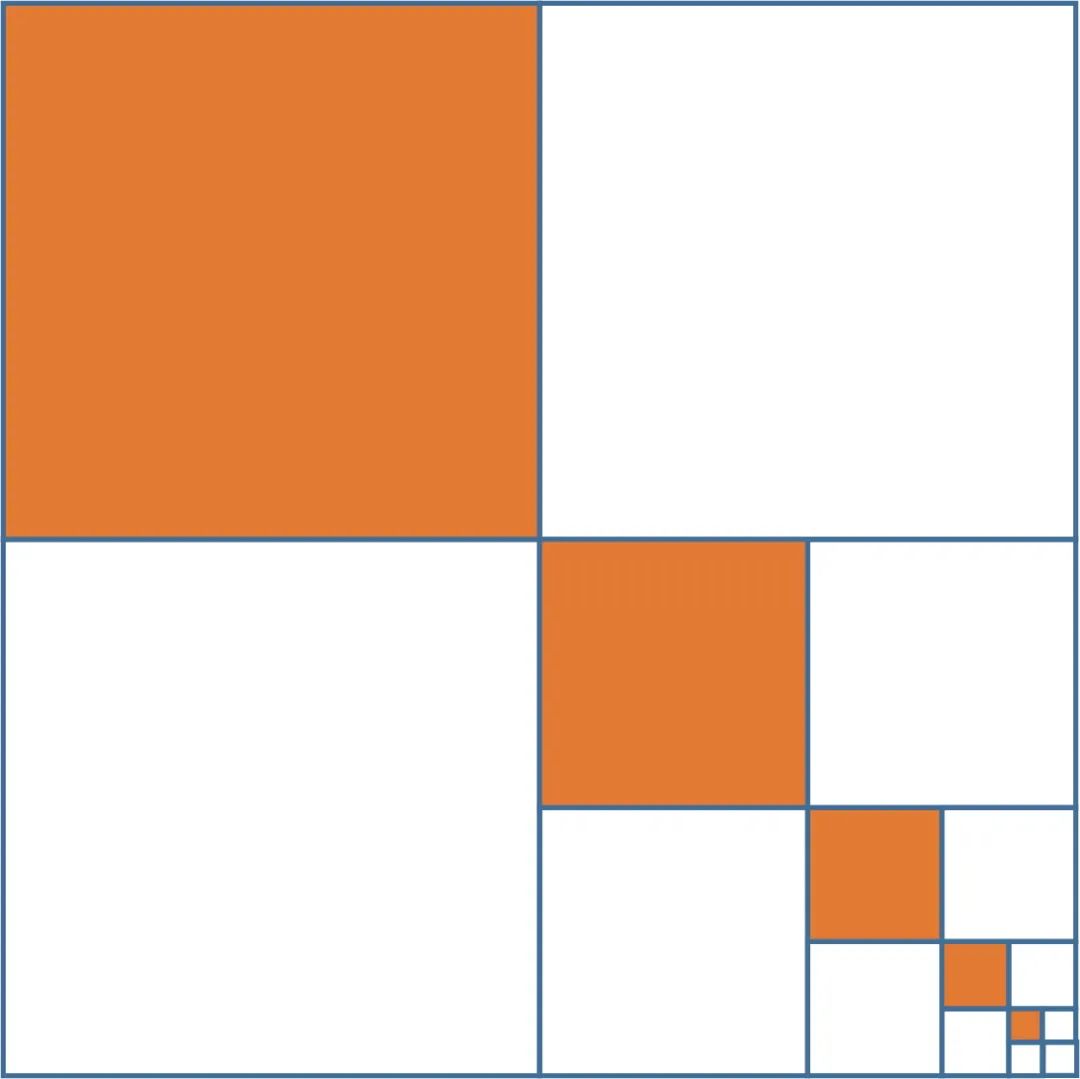
El enfoque más directo a este problema es usar sumas de series infinitas que los estudiantes de primaria no pueden entender. Si no necesita sumar la serie infinita, puede pensarlo de esta manera: después de eliminar el bloque 1/4 en la esquina inferior derecha, la parte restante es 1/3 de la cual está coloreada (como se muestra a la izquierda en la figura a continuación).
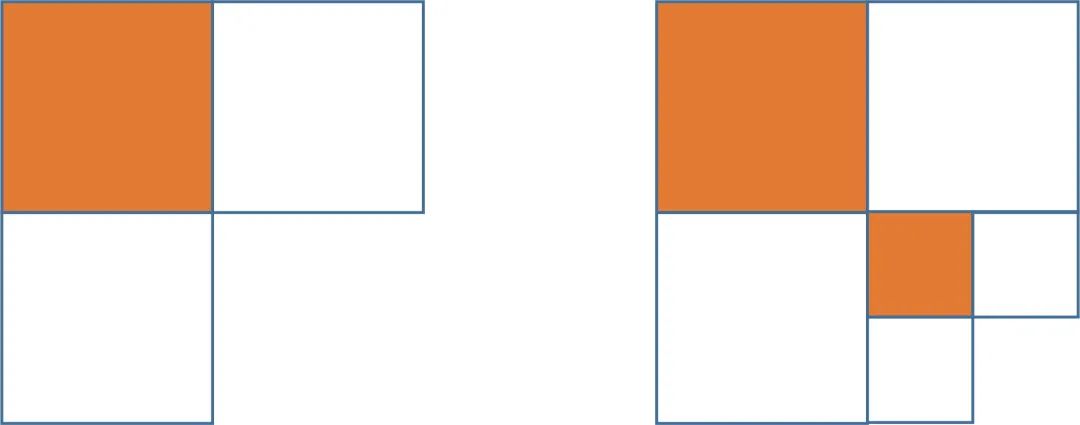
En el bloque de 1/4 restante, eliminamos la esquina inferior derecha de este bloque de 1/4, luego la parte pintada aún ocupa 1/3 de toda el área (como se muestra en la imagen de la derecha arriba). Por analogía, cada vez que se recorta una pequeña pieza en la esquina inferior derecha, el área de la parte pintada es 1/3 del área total en diferentes escalas, por lo que el área total de la parte pintada es 1/3 del área total del cuadrado.
Con base en esta idea, ¿podemos resolver el siguiente problema por analogía?
En el siguiente triángulo regular amarillo ABC, tome los puntos medios D, E y F de los tres lados y conéctelos respectivamente, luego tome los puntos medios H, I y G de los tres lados DE, EF y DF respectivamente, y pinte ΔDGH, ΔEHI y ΔGIF en azul. Luego, repita la misma operación anterior para el pequeño triángulo GHI en el medio. Si esta operación continúa para siempre, ¿qué fracción del área de todo el triángulo equilátero es el área de la parte coloreada en amarillo en la figura?
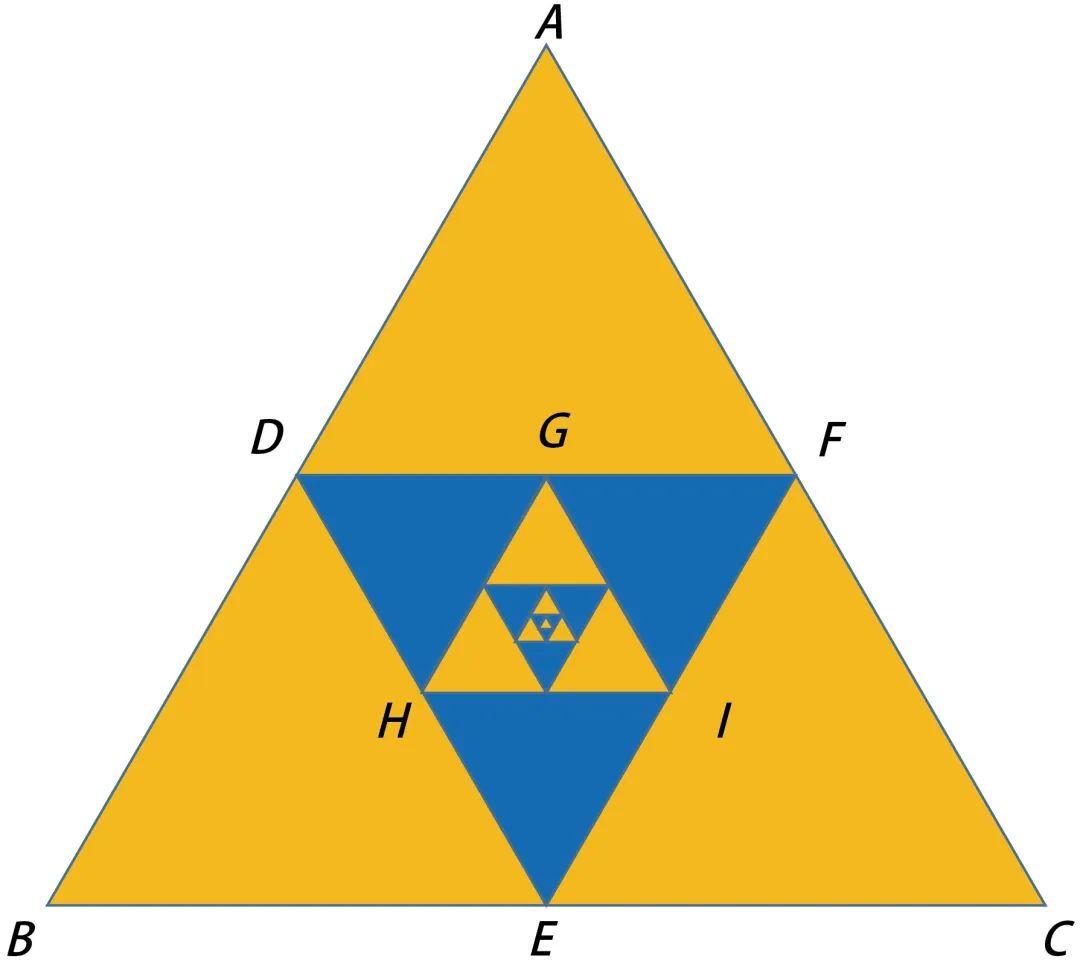
En este problema, el triángulo corresponde al cuadrado del problema anterior. En la solución del problema anterior, deducimos una parte de la parte ampliada que es igual a la figura original (es decir, el 1/4 de la esquina inferior derecha) del cuadrado. Correspondientemente, también encontramos la parte ampliada de la figura que es igual a la figura original, que obviamente es el triángulo correspondiente a GHI. Después de deducirla, la parte restante, la proporción del área amarilla es 12/15=4/5. Por lo tanto, la proporción de toda el área también es 4/5.
artículo dividido
Los términos divididos son una técnica común en las matemáticas de la escuela primaria y secundaria. En general, lo que se enseña en los libros de texto es el término dividido en fracciones más simple, y el numerador solo tiene dos términos multiplicados entre sí. Pero detrás subyace la idea básica de dividir: convertir un elemento en dos y restarlos, de modo que el anverso y el reverso puedan cancelarse.
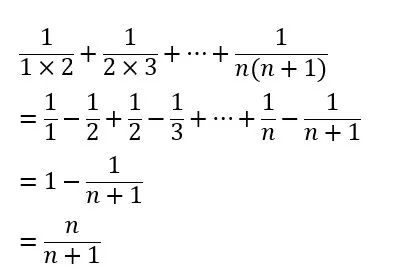
Luego, por analogía, también podemos dividir términos en fracciones cuyos denominadores se multiplican por tres, cuatro o más números aritméticamente diferentes.
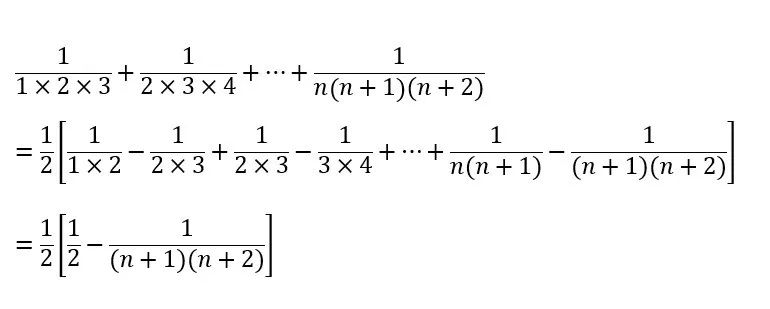
Además de los términos divididos fraccionarios, los productos enteros también pueden dividir términos:
1×2+2×3+...+n(n+1)
Podemos multiplicar dos números naturales y dividir el término en la diferencia de dos productos, cada producto es el producto de 3 números naturales, de la siguiente manera:
n(n+1)=[n(n+1)(n+2)-(n-1)n(n+1)]/3
¿Qué pasa si en lugar de multiplicar dos números naturales, se multiplican tres o más números naturales? Por ejemplo:
1×2×3+2×3×4+...+n(n+1)(n+2)
Usando la analogía del término dividido fraccionario y el término dividido entero anterior, no es difícil obtener el siguiente término dividido:
n(n+1)(n+2)=[n(n+1)(n+2)(n+3)-(n-1)n(n+1)(n+2)]/4
La línea recta divide el plano y el plano divide el espacio
Veamos una pregunta clásica de nuevo:
¿En cuántas partes pueden dividir n líneas rectas al plano?
Usando la idea de recursividad, sabemos que el número de bloques que n rectas dividen como máximo el plano es el número de bloques que n-1 rectas dividen como máximo el plano más n. Así, n rectas dividen el plano en 1+1+2+3+⋯+n=n(n+1)/2+1 bloques. Verifique el cálculo: cuando n=1, 2, 3, son 2, 4, 7 respectivamente, lo cual se cumple.
Por supuesto, resolver el problema aquí no es el final, el problema central aún no se ha resuelto.
La inducción que acabamos de hacer es solo una conjetura, y todavía tenemos que demostrar que es correcta. ¿Por qué el número máximo de bloques se divide entre n líneas rectas más n sobre la base del número máximo de bloques dividido entre n-1 líneas rectas? Se trata de la relación entre " línea-intersección-segmento de línea-plano ".
Sabemos que si hay n puntos en una línea recta, estos puntos dividirán la línea recta en n+1 segmentos.
Originalmente había n - 1 rectas. Después de agregar la n-ésima recta, la n-ésima recta tiene como máximo n-1 puntos de intersección con las n-1 rectas anteriores. Estos puntos de intersección dividirán la n-ésima recta en n segmentos. Y cada sección dividirá el área original en dos, por lo que hay n bloques más. La siguiente figura muestra un diagrama esquemático de n=3.
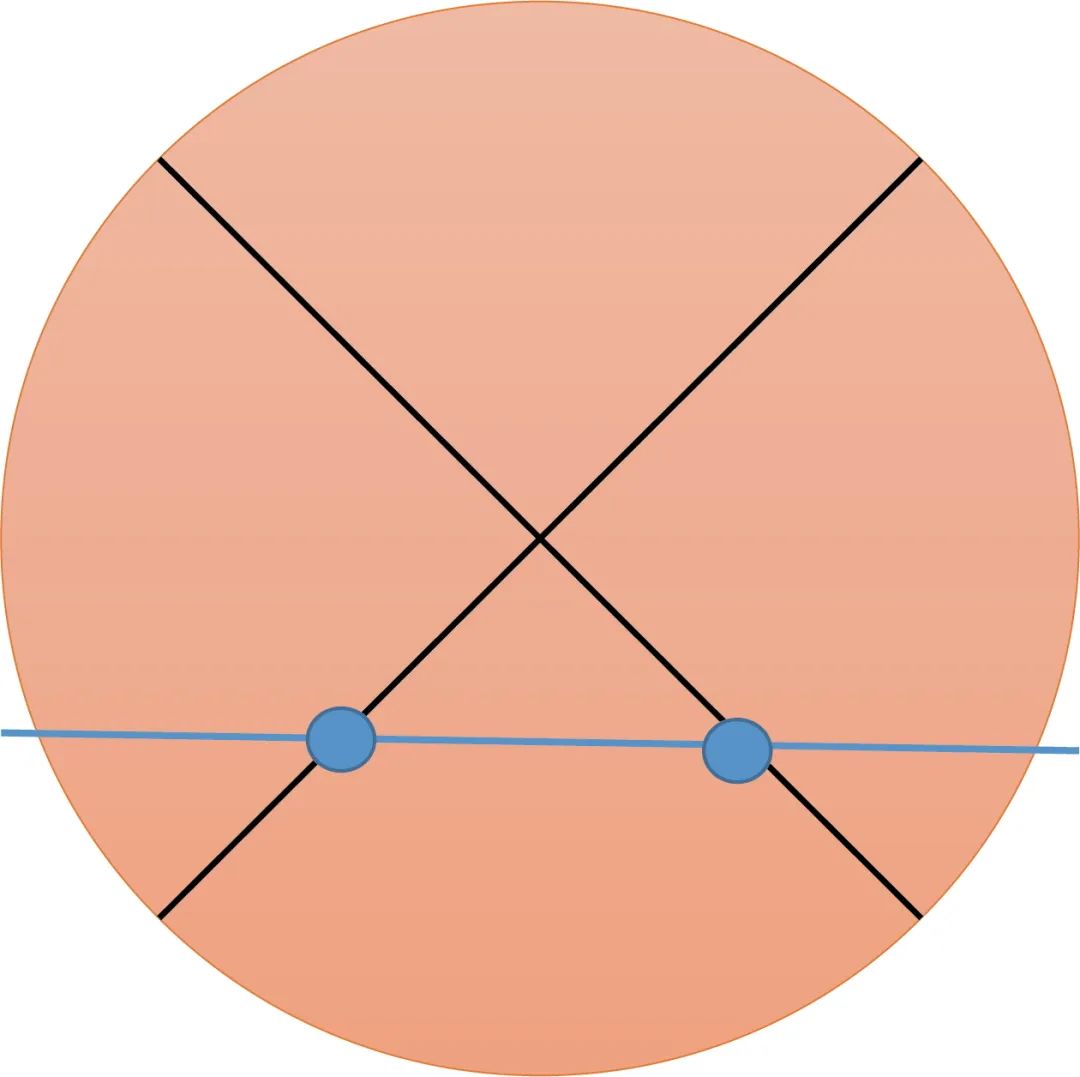
Podemos aplicar completamente este método de razonamiento al problema de dividir planos por gráficos de planos no lineales, como el siguiente problema:
¿En cuántas partes pueden n círculos dividir el plano como máximo?
Podemos seguir utilizando el pensamiento recursivo anterior y el método de análisis de "intersección-línea segmento-plano". Si se agrega un círculo sobre la base de n-1 círculos, entonces este círculo tiene como máximo 2 (n-1) puntos de intersección con los n-1 círculos anteriores (como se muestra en la figura a continuación, después de agregar el cuarto círculo rojo, se cruzará con los 3 círculos anteriores como máximo, y hay 6 puntos de intersección rojos en total).
Según esto, n círculos dividen el plano en como máximo:
1+1+2+4+…+2(n-1)=2+n(n-1) (n≥1)
Si agrega una dimensión, el problema se convierte en:
¿En cuántas partes pueden dividir n planos el espacio como máximo?
Si derivamos de la idea de que los puntos se dividen en líneas rectas en segmentos de línea, y los segmentos de línea en planos en regiones, encontraremos que la solución al problema de dividir un plano en un espacio también se puede comparar con el método de dividir una línea en un plano. Primero, tenemos que hacer algunas analogías conceptuales y operativas.
Conceptos y operaciones en 2D |
Conceptos y operaciones en 3D |
línea recta |
departamento |
Intersección |
línea de intersección |
Punto a línea en segmento de línea |
segmentos de recta en planos |
El segmento de línea divide el plano en el área del plano |
El avión divide el espacio en regiones espaciales. |
En el problema de dividir un plano por una recta, usamos el segmento de recta extra para analizar el número de planos que se dividen después de agregar una línea recta; luego, en el problema de dividir un espacio por un plano, ¿podemos usar también el plano extra para analizar el número de espacios que se dividen después de agregar un plano?
Todavía usamos el pensamiento recursivo. Sabemos que 3 planos dividen el plano en 8 partes como máximo. Añadir 1 plano sobre la base de 3 planos. Los primeros 3 planos tienen como máximo 3 líneas de intersección con este plano. Estas tres líneas de intersección dividirán el 4º plano en 7 partes como máximo (obtenidas de la conclusión de dividir el plano por una línea recta). Cada parte dividirá el espacio original en dos, por lo que se dividen 7 bloques más en base a 8 bloques.
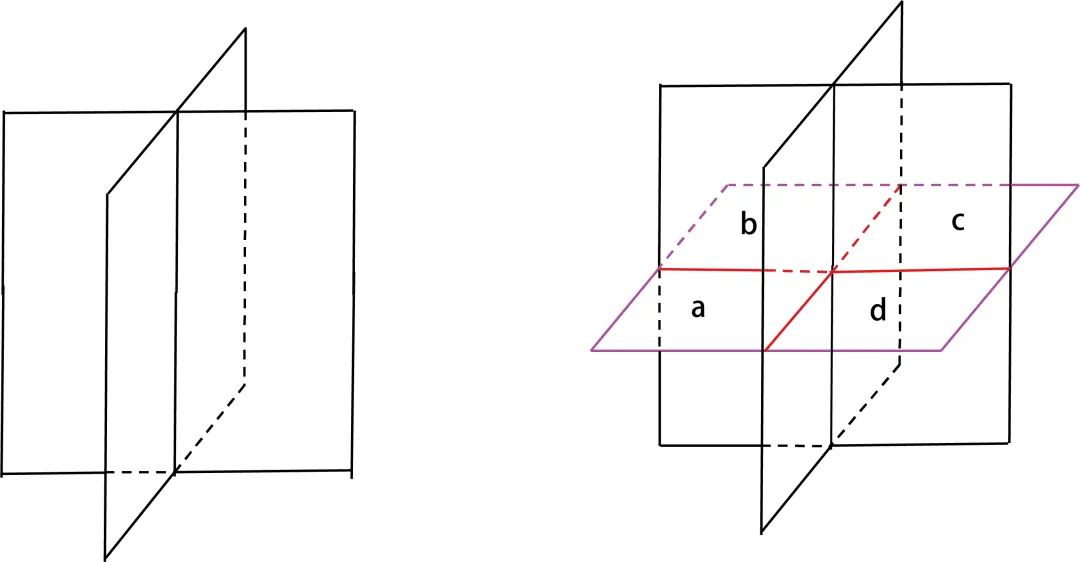
En términos generales, el n-ésimo plano tendrá n-1 líneas de intersección con los n-1 planos anteriores. Según la línea recta para dividir el plano, estas n-1 líneas de intersección pueden dividir el n-ésimo plano en n(n-1)/2+1 áreas como máximo, de modo que se pueden dividir n(n-1)/2+1 espacios más que n-1 planos.
Por tanto, el subespacio plano satisface la siguiente relación de recurrencia:
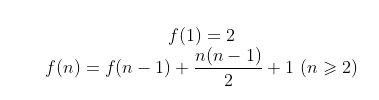
falta de analogía
Sin embargo, debido a que la base lógica del razonamiento analógico es insuficiente, probable y especulativa, sus conclusiones solo se sustentan en diversos grados y no necesariamente son completamente confiables. Por lo tanto, la analogía solo puede usarse como un medio auxiliar de descubrimiento, no como un método matemático estricto. Para las conclusiones extraídas mediante razonamiento analógico, se requieren demostraciones rigurosas para confirmar la exactitud de las conclusiones adivinadas.
Por ejemplo: "Esta novela tiene solo 1000 palabras y la escritura es fluida. Esta novela ganó un premio. La novela que escribiste también tiene 1000 palabras y la escritura es fluida, por lo que definitivamente ganarás el premio".
Históricamente, los argumentos de Thomas Reid a favor de la existencia de vida en otros planetas en el siglo XVIII también se basaron en el razonamiento por analogía. Reid señaló muchas similitudes entre la Tierra y los demás planetas del sistema solar: todos orbitan y están iluminados por el sol; varios planetas tienen lunas; todos giran sobre sus ejes. Por ello, concluye, “no es descabellado pensar que estos planetas puedan, como nuestra Tierra, ser hábitats de todo tipo de vida”. En última instancia, la ciencia moderna ha refutado esta analogía errónea. Sin embargo, aun así, los humanos todavía esperan usar analogías para encontrar planetas terrestres alienígenas adecuados para la vida.
No todo el mundo entiende realmente las analogías.
A estas alturas, muchas personas pueden pensar que la analogía ya es una forma de pensar que dominamos todos los días. ¿Pero es éste realmente el caso?
La novela "Flat Country" es una obra pionera en el siglo XIX que imagina un espacio de cuatro dimensiones. En la segunda mitad de la novela, el autor utiliza ampliamente el razonamiento analógico.
El protagonista que ha estado viviendo en el país plano una vez soñó con el país de la línea recta y trató de explicarle al rey del país de la línea recta lo que es un plano bidimensional, pero no importa cómo lo explicó, no pudo tener éxito y tuvo que darse por vencido.
Una vez, cuando el protagonista estaba explicando los conocimientos de geometría y aritmética a su nieto hexagonal, su nieto sabio le hizo una pregunta: Si mueves un punto 3 pulgadas, puedes obtener un segmento de línea de 3 pulgadas, que se puede registrar como 3; ), debes poder obtener otra figura (no sé qué figura es), la longitud de cada lado de esta figura también es de 3 pulgadas, y esta figura se debe registrar como un cubo de 3.
Aunque el nieto del protagonista ha estado viviendo en el país llano y nunca ha visto un cubo, ha previsto la existencia de un cubo a través de un razonamiento de pensamiento puro.Este método de razonamiento es el razonamiento analógico.
Es una pena que el protagonista no pueda romper el confinamiento del mundo bidimensional. A sus ojos, el cubo de 3 tiene solo un significado numérico, no un significado geométrico. Qué tonto, pensó, el chico.
Pero en ese momento llegó un visitante de un país del espacio. Así es como el visitante se describió a sí mismo: Desde cierto ángulo, soy de hecho un círculo. Soy un círculo más perfecto que cualquier otro círculo en Planilandia. Más precisamente, soy un círculo compuesto de muchos círculos.
Así es, este visitante es la pelota.
Para que el obstinado protagonista del libro comprendiera qué es la tercera dimensión, Ball también tomó la poderosa arma de la analogía.
El razonamiento analógico de Ball nos parece tan natural, es tan persuasivo:
1. Un punto se mueve hacia el norte y deja un rastro brillante.Este rastro se llama segmento de línea, y un segmento de línea tiene dos puntos finales.
2. Este segmento de línea norte-sur se mueve en paralelo en dirección este-oeste, por lo que cada punto en el segmento de línea dejará una trayectoria lineal en dirección este-oeste. Suponiendo que el segmento de línea se mueve una distancia igual a la longitud original del segmento de línea, entonces obtienes un cuadrado. Un cuadrado tiene cuatro lados y cuatro esquinas.
A este lugar, los protagonistas de Flatland pueden entender completamente.
Pero a continuación, la pelota quiere que el protagonista use su imaginación, imagine un cuadrado en el país llano moviéndose hacia arriba en paralelo, es decir, moviéndose fuera del país llano, de modo que cada punto en el cuadrado no pase por los lugares que otros puntos alguna vez ocuparon. La trayectoria dejada por cada punto es un segmento de línea que se pertenece solo a sí mismo.
Honestamente, es una muy buena analogía. Pero impotente, el protagonista que vive en el país plano no puede imaginar lo que es mudarse fuera del país plano, y está a punto de volverse loco. Pero aun así reprimió su impaciencia, y así tuvo la siguiente conversación.
Protagonista: Ya que dijiste que mover el cuadrado "hacia arriba" puede producir una nueva figura, ¿qué tipo de figura es esta figura? Supongo que siempre puedes describir esta figura en el idioma de Planilandia.
Pelota: esta forma es tan simple que solo puede deducirse por analogía estricta; solo que, dicho sea de paso, no puedes llamar a esta nueva forma "figura" porque es una forma tridimensional. Pero puedo describirte esta nueva forma. No puedo describirlo exactamente, pero la analogía les dará una idea de cómo se ve esta nueva forma.
Primero, supongamos que tenemos un punto. Como es un punto, por supuesto que solo tiene un vértice.
Al mover un punto, se puede obtener un segmento de línea. Un segmento de recta tiene 2 vértices.
Al mover un segmento de línea, se puede obtener un cuadrado y un cuadrado tiene 4 vértices.
Puedes responder las siguientes preguntas tú mismo: 1, 2, 4, esto es obviamente una progresión geométrica. Entonces, ¿cuál es el siguiente número de la serie?
Protagonista: 8.
Bola: Exacto. Entonces, al mover un cuadrado, se puede producir una nueva forma. Ahora no sabes el nombre de esta forma, pero la gente en nuestro país espacial lo llama "cubo". Un cubo tiene 8 vértices. ¿Ahora crees lo que digo?
Protagonista: Ya que dijiste que esta nueva forma tiene un "vértice", debe ser lo que llamamos una "esquina". Entonces, ¿esta cosa nueva también tiene lados?
Bola: Por supuesto que hay lados. Esto se puede deducir por analogía. Sin embargo, los lados de esta nueva forma no son lo que llamarías "lados", sino lo que llamaríamos "lados". Un lado equivale a una figura sólida en el país plano.
Protagonista: Entonces, ¿cuántas formas sólidas o cuántos lados tiene esta nueva forma?
Ball: ¿ Por qué todavía me preguntas? ¿No eres matemático? Con el debido respeto, permítanme ponerlo de esta manera: cualquier forma puede verse rodeada por algunos 'elementos laterales', y la dimensión de cada 'elemento lateral' es siempre 1 menor que la dimensión de la forma. Dado que 1 punto es de dimensión cero, los puntos no tienen 'elementos laterales'; y así sucesivamente, los segmentos de línea tienen 2 puntos laterales y los cuadrados tienen 4 lados; 0, 2, 4, ¿cómo llamas a esta serie?
Protagonista: Progresión aritmética.
Ball: Entonces, ¿cuál es el próximo número de esta serie?
Protagonista: 6.
Bola: Exacto. Verás, puedes responder esa pregunta tú mismo. El cubo creado al mover el cuadrado está delimitado por 6 lados, es decir, por 6 interiores tuyos. Ahora lo entiendes todo, ¿verdad?
Sin embargo, el protagonista no entiende. Se estaba volviendo loco, llamando "monstruo" y diciendo: "Ya seas un mentiroso, un mago, una pesadilla o un demonio, no puedo soportar más tus bromas".
Al final, la pelota no tuvo más remedio que entrar en acción, sacando al protagonista cuadrado del país plano y hacia el país del espacio. Ver para creer Después de experimentar un gran shock, el protagonista finalmente comprende que el país del espacio existe. En este momento, el protagonista que ha adquirido nuevos conocimientos parece estar en el cielo. Su mente estaba completamente encendida y ya no podía tolerar que algunas personas dictatoriales restringieran la dimensión a dos, tres o cualquier dimensión menos que infinita.
Por lo tanto, justo cuando la pelota quería continuar impartiendo el conocimiento de las reglas y las formas tridimensionales al protagonista, el protagonista se armó de valor para interrumpir la pelota y comenzó el siguiente diálogo.
Protagonista: Señor, es su sabiduría la que abre mi mente y enciende mi deseo. Me haces pensar que más allá de ti hay algo más grande, más hermoso, más perfecto. Eres una forma compuesta de muchos círculos, y eres más alto que todos los habitantes de nuestro país llano; entonces no hay duda de que por encima de ti, hay un ser supremo compuesto de muchas esferas, que será más alto que cualquier forma tridimensional del país del espacio. Ahora estamos mirando todo en el país plano en el país espacial, y podemos tener una vista panorámica del interior de todas las figuras planas; dado que este es el caso, debe haber un espacio más alto y más puro sobre nosotros; también debes planear llevarme allí para verlo. Ah, no importa en qué dimensión te encuentres, siempre serás mi maestro filosófico y mi amigo. Vayamos juntos a un lugar más alto, y pasemos por alto todo esto desde un espacio más amplio y una dimensión más profunda. Desde allí, podemos ver el interior del cubo, e incluso tu tripa, y las tripas de otras esferas como tú, no estarán obstruidas.
Inesperadamente, esta vez fue el turno de Qiu de quedarse estupefacto.
Ball: Pero, ¿dónde está el espacio de cuatro dimensiones que mencionaste?
Protagonista: No lo sé. Pero mentor, usted debe saber.
Bola: No lo sé. No existe tal lugar en absoluto. Tu idea es completamente inimaginable.
Protagonista : Podemos usar la analogía para demostrar la existencia de formas de cuatro dimensiones.
Pelota: ¡Analogía! ¡Disparates! ¡Qué analogía!
Protagonista: Su Excelencia debe estar probándome para ver si todavía recuerdo el apocalipsis que me transmitió.
En un espacio unidimensional, ¿el movimiento de un punto no produciría un segmento de línea con dos extremos?
En un espacio bidimensional, ¿no produciría un cuadrado con 4 vértices al mover un segmento de línea?
En el espacio tridimensional, ¿no produciría el movimiento de un cuadrado una criatura divina con 8 vértices, un cubo?
Entonces, en cuatro dimensiones, si mueves un cubo, ¿no produciría una criatura más divina con 16 vértices?
Verás, la ley de la secuencia nunca puede fallar: 2, 4, 8, 16, ¿no es una progresión geométrica? ¿No es ésta la conclusión de que 'sólo puede deducirse por estricta analogía'?
Un segmento de recta tiene 2 extremos, y un cuadrado tiene 4 lados, entonces un cubo debe tener 6 lados, ¿No es esto lo que me enseñó Vuestra Excelencia? Mira la ley de esta secuencia numérica: 2, 4, 6, ¿no es una progresión aritmética? Luego, en el siguiente paso, debemos ser capaces de sacar tal conclusión: en el espacio de cuatro dimensiones, la descendencia más sagrada nacida del cubo sagrado debe tener 8 lados, ¿no es así? ¿No es esto lo que me enseñaste, la conclusión de que "sólo se puede deducir por estricta analogía"?
En el espacio de cuatro dimensiones, un cubo se mueve en una nueva dirección. Por estricta analogía, cada punto del cubo pasa a través de un nuevo espacio, dejando trayectorias que no se superponen; esto crea una forma más perfecta que un cubo. Esta forma tiene 16 vértices, 16 ángulos sólidos y está rodeada por 8 lados del cubo.
La siguiente tabla resume las conclusiones de la analogía del protagonista.
dimensión |
nombre |
vértice |
forma de elemento lateral |
Número de elementos laterales |
1 |
segmento de línea |
2 |
punto |
2 |
2 |
cuadrado |
4 |
segmento de línea |
4 |
3 |
cubo |
8 |
cuadrado |
6 |
4 |
hipercubo |
dieciséis |
Cubo |
8 |
El protagonista no esperaba que esta vez la pelota fuera completamente inaceptable, y gritó una y otra vez para decirle al protagonista que se callara. Al final, pateó al protagonista de regreso a Flatland.
Después de leer esto, recordé una frase: los insectos de verano no pueden hablar hielo y las ranas no pueden hablar mar.
Nos reímos de las ranas de pozo, pero en realidad cada uno de nosotros es una rana de pozo. Si bien todos conocemos las analogías, no todos realmente las entienden y las usan. Podemos usar analogías para explicar lo que entendemos a un recién llegado dentro del alcance de nuestra propia cognición, pero es difícil aceptar conclusiones de analogías más allá de los límites de nuestra propia cognición o del entorno.
Lectura recomendada

Autor: 昍 papá, 昍 mamá
¿Cuál es la belleza de las matemáticas? ¿Dónde está la belleza de las matemáticas? Solo aprendiendo a apreciar la belleza de las matemáticas podemos realmente entender las matemáticas.
Muestra la belleza del pensamiento matemático equilibrado y ordenado, la belleza de la lógica concisa y precisa, la belleza intuitiva de medir todas las cosas y la belleza de la creación que explora los misterios.

