Esta columna contiene el conocimiento básico de la teoría y la codificación de la información, organizado por puntos de conocimiento, y se puede utilizar como referencia para la enseñanza o el aprendizaje. La versión de descuento se ha archivado en [repositorio de Github: https://github.com/timerring/information-theory ] o cuenta pública [AIShareLab] para responder a Information Theory .
Directorio de artículos
secuencia m (secuencia de registro de desplazamiento de retroalimentación lineal más larga)
Polinomios característicos de registros de desplazamiento de retroalimentación lineal
Relación de recurrencia del registro de desplazamiento de retroalimentación lineal
La relación de recurrencia también se denomina función lógica de retroalimentación o ecuación de recurrencia. Sea el estado inicial del registro de desplazamiento de retroalimentación lineal que se muestra en la Figura 2 ( a 0 a 1 … an − 2 an − 1 ) (a_{0} a_{1} \ldots a_{n-2} a_{n-1 })( un0a1…anorte - 2an − 1) , después de una retroalimentación lineal de desplazamiento, la entrada de la primera etapa en el extremo izquierdo del registro de desplazamiento es
an = c 1 an − 1 + c 2 an − 2 + ⋯ + cn − 1 a 1 + cna 0 = ∑ i = 1 nciano − i a_{n}=c_{1} a_{n-1}+c_{2} a_{n-2}+\cdots+c_{n-1} a_{1}+c_{n} a_{0} =\sum_{i=1}^{n} c_{i} a_{ni}an=C1an − 1+C2anorte - 2+⋯+Cn − 1a1+Cna0=yo = 1∑nCyoanorte - yo

Si por k \boldsymbol{k}K cambia, entonces la entrada de la primera etapa es
al = ∑ i = 1 ncial − i a_{l}=\sum_{i=1}^{n} c_{i} a_{li}ayo=yo = 1∑nCyoal - yo
Entre ellos, l = n + k − 1 ≥ n , k = 1 , 2 , 3 , … l=n+k-1 \geq n, k=1,2,3, \ldotsyo=norte+k−1≥n ,k=1 ,2 ,3 ,...
Se puede ver que la entrada de la primera etapa del registro de desplazamiento está determinada por la lógica de retroalimentación y el estado original del registro de desplazamiento. La fórmula anterior se llama relación de recurrencia.
Polinomios característicos de registros de desplazamiento de retroalimentación lineal
Utilice el polinomio f(x) para describir el estado de conexión de retroalimentación del registro de desplazamiento de retroalimentación lineal:
f ( x ) = c 0 + c 1 x + ⋯ + cnxn = ∑ i = 0 ncixif(x)=c_{0}+ c_{ 1} x+\cdots+c_{n} x^{n}=\sum_{i=0}^{n} c_{i} x^{i}f ( x )=C0+C1X+⋯+CnXnorte=yo = 0∑nCyoXi
se llama polinomio característico o ecuación característica. Entre ellos,xix^{i}Xi existe, indicando queci = 1 c_{i}=\mathbf{1}Cyo=1 , de lo contrarioci = 0 c_{i}=\mathbf{0}Cyo=0 , el valor de x en sí mismo no tiene significado práctico. ci c_{i}CyoEl valor de determina la conexión de retroalimentación del registro de desplazamiento. Dado que c 0 = cn = 1 c_{0}=c_{n}=1C0=Cn=1 , por lo tanto, f(x) es un polinomio de grado n con un término constante de 1, y n es el número de etapas del registro de desplazamiento.
Una condición necesaria y suficiente para que un registro de desplazamiento de realimentación lineal de n niveles genere m secuencias es que su polinomio característico sea un polinomio primitivo de grado n. Si un polinomio f(x) de grado n satisface las siguientes condiciones:
(1) f(x) es un polinomio reducido (es decir, un polinomio que no se puede factorizar);
(2) f(x) es divisible por ( xp + 1 ) , pn − 1 (x^{p}+1), p^{n}-1( Xpag+1 ) ,pagnorte−1 ;
(3) f(x) es indivisible ( xq + 1 ) , q < p (x^{q+1}), q \lt p( Xq + 1 ),q<pag _
Entonces f(x) se llama polinomio primitivo. Lo anterior proporciona una base teórica para que formemos la secuencia m.
generador de secuencia m
El generador de secuencias m se compone de un registro de desplazamiento de retroalimentación lineal, la clave es determinar el estado de la línea de retroalimentación mediante el polinomio característico f(x), y el polinomio característico f(x) debe ser un polinomio primitivo.
Ahora tome n=4 como ejemplo para ilustrar la composición del generador de secuencia m. La secuencia m generada por el registro de desplazamiento de retroalimentación lineal de 4 etapas tiene un período de p = 2 4 − 1 = 15 p=2^{4}-1=15pag=24−1=15 , su polinomio característico f(x) es un polinomio primitivo de grado 4, que puede ser divisible por( x 15 + 1 ) (x^{15}+1)( X15+1 ) . Primero ponga( x 15 + 1 ) (x^{15}+1)( X15+1 ) Descomponga los factores para que cada factor sea un polinomio reducido y luego encuentre f(x).
x 15 + 1 = ( x + 1 ) ( x 2 + x + 1 ) ( x 4 + x + 1 ) ⋅ ( x 4 + x 3 + 1 ) ( x 4 + x 3 + x 2 + x + 1 ) \begin{alineado} x^{15}+1 & =(x+1)(x^{2}+x+1)(x^{4}+x+1) \\ & \cdot(x^{ 4}+x^{3}+1)(x^{4}+x^{3}+x^{2}+x+1) \end{alineado}X15+1=( X+1 ) ( X2+X+1 ) ( X4+X+1 )⋅( X4+X3+1 ) ( X4+X3+X2+X+1 )
Entre ellos, hay 3 polinomios de grado 4, pero ( x 4 + x 3 + x 2 + x + 1 ) (x^{4}+x^{3}+x^{2}+x+1)( X4+X3+X2+X+1 ) es divisible por( x 5 + 1 ) (x^{5}+1)( X5+1 ) , por lo que no es un polinomio primitivo. Así que encuentra dos polinomios primitivos de grado 4( x 4 + x + 1 ) (x^{4}+x+1)( X4+X+1 ) y(x4 + x3 + 1) (x^{4}+x^{3}+1)( X4+X3+1 ) . Cualquiera de ellos puede generar m-secuencias. Usaf ( x ) = ( x 4 + x + 1 ) \mathrm{f}(\mathrm{x})=(\mathrm{x}^{4}+\mathrm{x}+\mathbf{1})f ( x )=( X4+X+1 ) m \mathrm{m}formadoEl generador de secuencia m se muestra en la figura.

Sea el estado inicial del registro de desplazamiento de 4 etapas 1000, c 4 = c 1 = c 0 = 1 , c 3 = c 2 = 0 c_{4}=c_{1}=c_{0}=1, c_ {3}=c_{2}=0C4=C1=C0=1 ,C3=C2=0 _ secuencia de salida{ ak } \{a_{k}\}{ unk} tiene una longitud de ciclo de 15.

Propiedades de las secuencias m
Características de equilibrio (balance)
El número de 1 en cada ciclo de la secuencia m es 1 más que el número de 0. Dado que p = 2 n − 1 p=2^{n}-1pag=2norte−1 es un número impar, por lo que el número de 1 en cada ciclo es( p + 1 ) / 2 = 2 n − 1 (p+1) / 2=2^{n-1}( pag+1 ) /2=2n − 1 (número par), y el número de 0 es( p − 1 ) / 2 = 2 n − 1 − 1 (p-1) / 2=2^{n-1}-1( pag−1 ) /2=2norte - 1−1 (número impar). En el ejemplo anterior, p=15, el número 1 es 8 y el número 0 es 7. Cuando p es lo suficientemente grande, el número de ocurrencias de 1 y 0 en un ciclo es básicamente igual.
Propiedades de longitud de ejecución (aleatoriedad de la distribución de longitud de ejecución)
Llamamos elementos en una secuencia que tienen el mismo valor (1 o 0) conectados entre sí como una ejecución. El número de elementos en una ejecución se denomina longitud de ejecución. Por ejemplo, m \boldsymbol{m} dado en la figurasecuencia m
Entre los 15 elementos de un ciclo, hay 8 longitudes de ejecución en total
: 1 longitud de ejecución con longitud 4, es decir, 1111;
1 longitud de ejecución con longitud 3, es decir, 000;
2 longitudes de ejecución con longitud 2, es decir, 11 y 00
; Hay 4 corridas de 1, es decir, 2 1s y 2 0s.
Un período de secuencia m ( p = 2 n − 1 ) (p=2^{n-1})( pag=2n − 1 ), el número total de carreras es2 n − 1 2^{n-1}2norte - 1 _
El número de ejecuciones de longitud 1 representa 1/2 del número total de ejecuciones; el número de ejecuciones de longitud 2 representa 1/2 del número total de ejecuciones 2 = 1/4 1/2^{2} = 1 / 41/ 22=1/4 ; El número de carreras con longitud 3 representa 1 / 2 del número total de carreras3 = 1 / 8 1 / 2^{3}=1 / 81/ 23=1/8 y así sucesivamente.
Generalmente, el número de corridas de longitud k representa 1/2 del número total de corridas k = 2 − k 1/2^{k}=2^{-k}1/ 2k=2− k , donde 11≤k≤( n−2 ) . Además, en las ejecuciones de longitud k, las ejecuciones con 1 y las ejecuciones con 0 representan cada una la mitad, la ejecución con longitud (n-1) es la ejecución con 0 y la ejecución con longitud n es la ejecución con 1.
Función Shift-add (superposición lineal)
m \boldsymbol{m}La secuencia obtenida después de sumar la secuencia m y su secuencia de desplazamiento módulo 2 sigue siendo lam \boldsymbol{m}Una secuencia de desplazamiento de la secuencia m . Deja queel señor m_{r}metrores la secuencia m mp m_{p} con periodo pmetropagLa secuencia después de r veces el cambio de retraso, entonces
mp ⊕ mr = ms m_{p} \oplus m_{r}=m_{s}metropag⊕metror=metros
Entre ellos, ms m_{s}metrospara mp m_{p}metropagSecuencia después de un cierto cambio de retraso. Por ejemplo,
mp = 000111101011001, … m_{p}=000111101011001, \ldotsmetropag=000111101011001 ,…
MP m_{p}metropagmr m_{r} después de un retraso de dos dígitosmetror, 再模二相加
mr = 010001111010 ms = mp ⊕ mr = 010110 , … \begin{array}{l} m_{r}=\mathbf{0} 10001111010 \\ m_{\mathrm{s}}=\boldsymbol {m}_{\mathrm{p}} \oplus \boldsymbol{m}_{r}=\mathbf{0} 10110, \ldots \end{matriz}metror=0 10001111010metros=metropag⊕metror=0 10110 ,…
Visible, ms = mp ⊕ mr m_{\mathrm{s}}=m_{\mathrm{p}} \oplus m_{r}metros=metropag⊕metrorpara mp m_{p}metropagSecuencia tras retardo de 8 bits.
propiedades de autocorrelación
m \boldsymbol{m}La secuencia m tiene propiedades de autocorrelación muy importantes. enm \boldsymbol{m}En la secuencia m , +1 se usa a menudo para representar 0 y -1 se usa para representar 1. Defina en este momento: m \boldsymbol{m}cuya longitud es pm序列, 记作
a 1 , a 2 , a 3 , … , ap ( p = 2 n − 1 ) a_{1}, a_{2}, a_{3}, \ldots, a_{p}(p= 2^{n-1})a1,a2,a3,…,apag( pag=2n − 1 )
a través dej \boldsymbol{j}Después de j cambios, m \boldsymbol{m}m序列为
aj + 1 , aj + 2 , aj + 3 , … , aj + p a_{j+1}, a_{j+2}, a_{j+3}, \ldots, a_{j+p}aj + 1,aj + 2,aj + 3,…,aj + pa
Entre ellos, ai + p = ai a_{i+p}=a_{i}ayo + pa=ayo(con p como el período), los elementos correspondientes de las dos secuencias anteriores se multiplican y luego se suman, y la suma resultante es
a 1 ⋅ aj + 1 + a 2 ⋅ aj + 2 + a 3 ⋅ aj + 3 + ⋯ + ap ⋅ aj + p = ∑ i = 1 paiaj + i a_{1} \cdot a_{j+1}+a_{2} \cdot a_{j+2}+a_{3} \cdot a_{j+3 }+\cdots +a_{p} \cdot a_{j+p}=\sum_{i=1}^{p} a_{i} a_{j+i}a1⋅aj + 1+a2⋅aj + 2+a3⋅aj + 3+⋯+apag⋅aj + pa=yo = 1∑pagayoaj + yo
Para medir el grado de correlación entre una secuencia m y su secuencia de desplazamiento j, y llamarlo m \boldsymbol{m}m序列( a 1 , a 2 , a 3 , … , ap ) (a_{1}, a_{2}, a_{3}, \ldots, a_{p})( un1,a2,a3,…,apag) función de autocorrelación. Escribe
R ( j ) = ∑ i = 1 paiaj + i R(j)=\sum_{i=1}^{p} a_{i} a_{j+i}R ( j )=yo = 1∑pagayoaj + yo
Cuando los números binarios 0 y 1 se utilizan para representar posibles valores de símbolos, la fórmula anterior se puede expresar como
R ( j ) = A − DA + D = A − D p R(j)=\frac{AD}{ A+D }=\frac{AD}{p}R ( j )=A+DA−D=pagA−D
En la fórmula, A y D son respectivamente m \boldsymbol{m}El número de elementos correspondientes a elementos iguales o diferentes de la secuencia m
y su secuencia desplazada en el tiempo j en un período también se puede reescribir como el número de R ( j ) = [ ai ⊕ ai + j = 0 ] − [ ai ⊕ ai + j = 1 ] el número p R(j)=\frac{[a_{i} \oplus a_{i+j}=0] \text {el número}-[a_{i} \oplus a_ {i+j}= 1] \text { número de }}{p}R ( j )=pag[ unyo⊕ayo + j=0 ] número de −[ unyo⊕ayo + j=1 ] número
De acuerdo con la función shift-and-add, ai ⊕ ai + j a_{i} \oplus a_{i+j}ayo⊕ayo + jTodavía es un elemento en la secuencia m, por lo que el numerador de la fórmula es igual a la diferencia entre el número 0 y el número 1 en un período de la secuencia m. También por m \boldsymbol{m}El balance de la secuencia m muestra que el número 0 es uno menos que el número 1 en un período, por lo queA − D = − 1 AD=- 1A−D=− 1 (cuando j es un número entero distinto de cero) o p (cuando j es cero). Entonces
R ( j ) = { 1 j = 0 − 1 pj = ± 1 , ± 2 , ... , ± ( pag − 1 ) . R(j)=\{\begin{array}{ll} 1 & j= 0 \\ \frac{-1}{p} & j=\pm 1, \pm 2, \ldots, \pm(p-1) \end{matriz}.R ( j )={
1pag− 1j=0j=± 1 ,± 2 ,…,± ( pag−1 ).
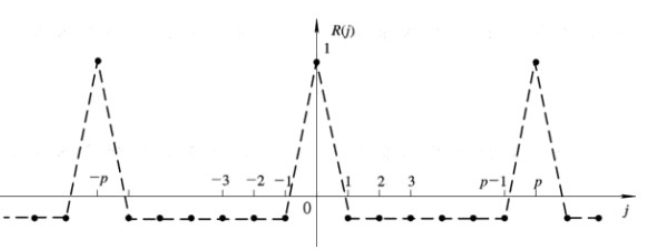
m \mathrm{m}La función de autocorrelación de la secuencia m tiene solo dos valores (1 y -1/p). R(j) es una función periódica, es decir,
R ( j ) = R ( j + kp ) \boldsymbol{R}(j)=\boldsymbol{R}(j+kp)R ( j )=R (j+k pag )
dondek = 1 , 2 , ... , pag = ( 2 norte - 1 ) k=1,2, \ldots, p=(2^{n}-1)k=1 ,2 ,…,pag=( 2norte−1 ) es el período. YR ( j ) R ( j )R ( j ) es una función par, es decir,
R ( j ) = R ( − j ) j = entero R(j)=R(-j) \quad j=\text { entero}R ( j )=R ( -j ) _j= entero
Características de pseudo-ruido
Si muestreamos una distribución normal de ruido blanco, si el valor muestreado es positivo, se registra como +1,
Si el valor de muestreo es negativo, regístrelo como -1 y organice la polaridad de cada muestreo en una secuencia, que se puede escribir como...+1,-1,+1,+1,+1,-1, -1,+1,- 1,…
Esta es una secuencia aleatoria, que tiene las siguientes propiedades básicas: (1) La probabilidad de que aparezcan +1 y -1 en la secuencia es igual;
Las series de longitud 1 en la secuencia representan aproximadamente 1 / 2 , las series de longitud 2 representan aproximadamente 1 / 4 , las series de longitud 3 representan aproximadamente 1 / 8, … \ ldots… Generalmente, la longitud esk \mathrm{k}La ejecución de k toma alrededor de 1/2 k 1/2^{k}1/ 2k , y el número de ejecuciones +1 y -1 es igual a la mitad;
Dado que el espectro de potencia del ruido blanco es constante, su función de autocorrelación es una función de impulso δ ( τ ) \delta(\tau)δ ( τ )。 把m \boldsymbol{m}La secuencia m se compara con la secuencia aleatoria anterior, cuando la duración del ciclop \boldsymbol{p}Cuando p es lo suficientemente grande,m \boldsymbol{m}Las propiedades de la secuencia m y la secuencia aleatoria son muy similares. Visible,m \boldsymbol{m}La secuencia m es una secuencia pseudoaleatoria con buenas características pseudoacústicas y es fácil de generar, por lo que es ampliamente utilizada.
referencias:
- Proakis, John G., et al. Ingeniería de sistemas de comunicación . vol. 2. Nueva Jersey: Prentice Hall, 1994.
- Proakis, John G., et al. MANUAL DE SOLUCIONES Ingeniería de Sistemas de Comunicación . vol. 2. Nueva Jersey: Prentice Hall, 1994.
- Zhou Jiongpan. Principios de la comunicación (3.ª edición) [M]. Beijing: Prensa de la Universidad de Correos y Telecomunicaciones de Beijing, 2008.
- Fan Changxin, Cao Lina. Principios de comunicación (7.ª edición) [M]. Beijing: National Defense Industry Press, 2012.