El método de suavizado tomó casi un mes para explicar y simular el algoritmo. La explicación es muy detallada en mi opinión, y el código y el principio son relativamente simples de entender, y el código casi no es difícil de implementar. Si no tiene ninguna sugerencia para comprender o dominar en detalle los algoritmos de análisis de series temporales, puede suscribirse a mi columna: Aprendizaje rápido de un texto: modelos comunes para el modelado matemático . Los modelos de análisis y predicción involucrados en cada escena están básicamente disponibles, y todos los métodos del método de suavizado son:

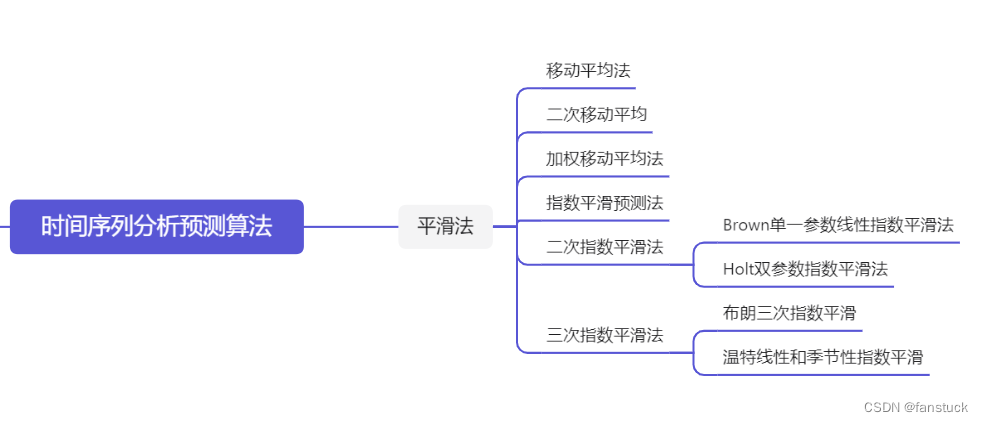
están incluidos. A continuación, estudiaremos y derivaremos el algoritmo de pronóstico de series temporales estacionarias. Sin embargo, la teoría básica del algoritmo de pronóstico de series temporales estacionarias es bastante compleja y necesitamos tener una cierta comprensión de la teoría básica para dominar el algoritmo más fácilmente. Por lo tanto, en el primer capítulo de nuestra apertura, primero comprenderemos todo el conocimiento teórico.

Espero que los lectores puedan cometer errores u opiniones en el área de comentarios después de leer, y los bloggers mantendrán el blog durante mucho tiempo y lo actualizarán a tiempo.

1. Algoritmo de pronóstico de series temporales estacionarias

La estacionariedad aquí se refiere a la estacionariedad amplia , que se caracteriza por el hecho de que las propiedades estadísticas de la secuencia no cambian con la traducción del tiempo, es decir, la media y la covarianza no cambian con la traducción del tiempo . La serie de tiempo se refiere a una secuencia formada por la disposición de los valores de un determinado indicador estadístico de un determinado fenómeno en diferentes momentos en orden cronológico. Serie de tiempo estacionaria En términos generales, se dice que una serie de tiempo es estacionaria si no hay un cambio sistemático en la media (sin tendencia), ningún cambio sistemático en la varianza y los cambios periódicos se eliminan estrictamente.

Las series de tiempo estacionarias son el tipo especial más importante de análisis de series de tiempo. Hasta el momento, el análisis de series temporales se basa básicamente en series temporales estacionarias, y sus métodos y teorías se limitan al análisis estadístico de series temporales no estacionarias.

Aquí necesitamos entender las propiedades básicas sobre la serie de tiempo y la distribución de los puntos correspondientes:

1. Funciones de distribución, media y covarianza de series temporales

Distribuciones de probabilidad

Dado que generalmente es imposible determinar la función de distribución de las series temporales, las personas prestan más atención a la descripción de varias cantidades características de las series temporales, como la función media, la función de covarianza, la función de autocorrelación, la función de autocorrelación parcial, etc. Estas cantidades características pueden a menudo representan al azar Las principales características de la variable.

función media

$\izquierda \{ X_{t},t=0,t=(-1,1),t=(-2,2),..., \derecha \}$ La función media de una serie de tiempo es:

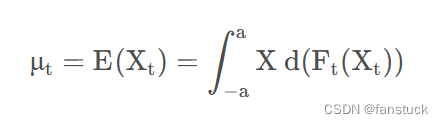
$\mu _{t}$ es la $\izquierda \{X_{t} \derecha \}$ función media, que es esencialmente una serie de números reales, y la media representa el centro oscilante del proceso aleatorio en cada momento.

función de autocovarianza

simetría: $\gamma (t,s)=\gamma (s,t)$

función de autocorrelación

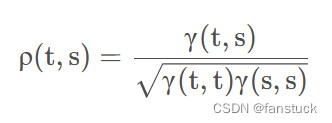
La función de autocorrelación describe la $\izquierda \{X_{t} \derecha \}$ estructura de correlación de la propia serie temporal. La función de autocorrelación de la serie de tiempo es simétrica y tiene $p(t,t)=1$

2. Funciones de autocovarianza y autocorrelación de series estacionarias

función de autocovarianza

Si $\izquierda \{X_{t} \derecha \}$ se trata de una sucesión estacionaria, suponiendo $EX_{t}=0$ que podemos usar la siguiente notación para representar la función de autocovarianza de una sucesión estacionaria:

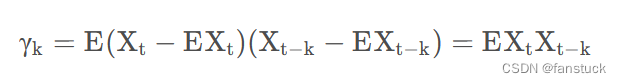
función de autocorrelación

En consecuencia, la función de autocorrelación de series estrictamente estacionarias se escribe como:

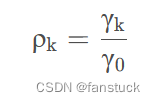
Propiedades de secuencias de autocovarianza y secuencias de función de autocorrelación para secuencias estacionarias

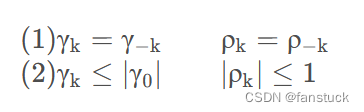
Las series de tiempo estacionarias se pueden dividir en series de tiempo estrictamente estacionarias y series de tiempo estacionarias amplias.

3. Series de tiempo estrictamente estacionarias

Si para cualesquiera n valores del tiempo t , la distribución conjunta $t_{1}<t_{2}<...<t_{n}$ de variables aleatorias en la secuencia es independiente del entero S, es decir: $X_{t_{1}+S},X_{t_{2}+S}...,X_{t_{n}+S}$

Se $X_{t}$ denomina serie temporal estrictamente estacionaria/estrechamente estacionaria/fuertemente estacionaria. Una distribución de probabilidad estrictamente estacionaria es independiente del tiempo.

4. Amplia serie temporal estacionaria

Por ejemplo, la serie temporal tiene una matriz finita de segundo orden y $X_{t}$ se cumplen las dos condiciones siguientes:

La serie de tiempo se denomina proceso ampliamente estacionario.
La media de cada variable aleatoria en un proceso ampliamente estacionario es constante y la covarianza de dos variables cualesquiera solo está relacionada con el intervalo de tiempo $(t)$ .

5. Contacto y distinción

conectar

Si una sucesión es estrictamente estacionaria y tiene una matriz de segundo orden finita, entonces la sucesión también debe ser ampliamente estacionaria.
Si la serie de tiempo es una serie normal (es decir, cualquier distribución de dimensión finita es una distribución normal), entonces la serie es una secuencia estrictamente estacionaria y una secuencia ampliamente estacionaria es equivalente entre sí.

la diferencia

Una distribución de probabilidad estrictamente estacionaria es invariable en el tiempo, y la media y la autocovarianza de una serie ampliamente estacionaria son invariantes en el tiempo.
Una secuencia estrictamente estacionaria no es necesariamente una secuencia ampliamente estacionaria; una secuencia ampliamente estacionaria no es necesariamente estrictamente estacionaria.

La serie de tiempo estacionaria discutida en la práctica es una serie de tiempo estacionaria amplia, lo que significa que en cualquier momento, la media y la varianza de la secuencia existen y son constantes, y la función de autocovarianza y el coeficiente de autocorrelación solo están relacionados con el intervalo de tiempo k. Solo las series de tiempo estacionarias se pueden usar para el análisis estadístico, porque la estacionariedad garantiza que los datos de la serie de tiempo sean todos de la misma distribución. Se puede usar una prueba de raíz unitaria para probar la estacionariedad de una serie de tiempo.

Si no hay correlación entre los valores de secuencia de una serie de tiempo estacionaria, significa que no hay regularidad en los datos antes y después, y no se puede extraer información efectiva.Este tipo de secuencia se denomina secuencia aleatoria pura. Entre las secuencias aleatorias puras, existe una secuencia denominada secuencia de ruido blanco, que es aleatoria y la varianza de cada periodo es constante. El análisis de series de tiempo estacionarias consiste en extraer completamente la relación entre las series de tiempo. Después de extraer la relación en la serie de tiempo, la secuencia restante debe ser una secuencia de ruido blanco .

6. Secuencia de ruido blanco

definición

Si la serie temporal $\izquierda \{X_{t} \derecha \}$ cumple las siguientes propiedades:

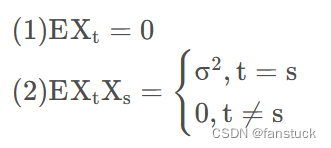
Entonces esta secuencia se llama secuencia de ruido blanco.
La secuencia de ruido blanco es un tipo especial de secuencia estacionaria amplia y también es la secuencia estacionaria más simple.

7. Secuencias IID

definición

Si $\izquierda \{X_{t} \derecha \}$ las variables aleatorias en la serie de tiempo $X_{t}$ son variables aleatorias independientes y $X_{t}$ tienen la misma distribución (cuando $X_{t}$ hay un primer momento, a menudo se asume $EX_{t}=0$ ), entonces se $\izquierda \{X_{t} \derecha \}$ llama secuencia independiente e idénticamente distribuida.

La secuencia IID $\izquierda \{X_{t} \derecha \}$ es una secuencia estrictamente estacionaria
En términos generales, la secuencia de ruido blanco y la secuencia IID son dos secuencias diferentes.
Pero cuando la secuencia de ruido blanco es una secuencia normal, también es una secuencia independiente e idénticamente distribuida, en este momento la llamamos secuencia de ruido blanco normal.

En segundo lugar, el modelo autorregresivo (Modelo autorregresivo , denominado AR)

definición

Un modelo autorregresivo es un método estadístico para manejar series de tiempo.Utiliza la misma variable, como los períodos anteriores de x, $x_{1}$ para $x_{t-1}$ predecir $x_{t}$ el desempeño del período actual, y asume una relación lineal entre ellos. Debido a que esto se desarrolla a partir de la regresión lineal en el análisis de regresión, pero en lugar de predecir y a partir de x, use x para predecir x (auto), por lo que se llama autorregresión .

Se sigue el coeficiente de autocorrelación del modelo autorregresivo de orden p y se trunca el coeficiente de autocorrelación parcial de orden p.

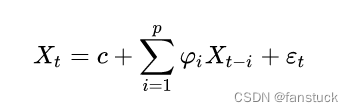
donde: c es un término constante; se supone que es un valor de error aleatorio $\varepsilon _{t}$ con media igual a 0 y desviación estándar igual a ; se supone que es constante para cualquier t. $\sigma$ $\sigma$

La descripción del texto es: el valor esperado de X es igual a una combinación lineal de uno o más períodos de retraso, más un término constante, más errores aleatorios.

Pasos de modelado

primer paso:

La detección de ruido blanco se realiza en la acumulación de tiempo. Si se determina que la secuencia es ruido blanco después de la inspección, no hay regularidad en los datos antes y después, y no se puede extraer información efectiva. Continúe solo si la detección no es una secuencia de ruido blanco.

Paso 2:

Verifique la estacionariedad de la secuencia, si la prueba considera que no es estacionaria, luego realice el procesamiento estacionario de la secuencia y vaya al primer paso; de lo contrario, vaya al tercer paso;

tercer paso:

Identifique el modelo, estime sus parámetros y vaya al cuarto paso;

el cuarto paso:

Probar la aplicabilidad del modelo, si pasa la prueba se puede obtener el modelo ajustado y se puede predecir la secuencia, de lo contrario pasar al tercer paso;

Decisión modelo

Para la serie de tiempo observada, si se determina que no es ruido blanco a través de la detección de ruido blanco y se determina que es estacionario después de la prueba de estacionariedad, el modelo a menudo se identifica de acuerdo con el coeficiente de correlación y el coeficiente de correlación parcial. Determine si el problema es adecuado para el modelado de modelos AR y determine aproximadamente el orden p.

Calculando el coeficiente de autocorrelación SAF , y el coeficiente de correlación parcial PACF .

Si una serie temporal cumple las dos condiciones siguientes:

ACF está siguiendo, es decir, ACF(k) no se convierte en 0 después de que k es mayor que alguna constante.
PACF se trunca, es decir, PACF(k) se convierte en 0 cuando k>p. ( Utilizado para determinar el orden, PACF no es estrictamente 0 después del retraso del pedido p, pero fluctúa en un rango pequeño alrededor de 0 )

Entonces puedes probar el modelo AR.

Realización de casos

La autorregresión se implementa en Python usando AutoReg en el paquete statsmodels.tsa.ar_model.

from statsmodels.tsa.ar_model import AutoReg

Los parámetros de esta función son:

ar_model = AutoReg(endog,
                   lags,
                   trend='c',
                   seasonal=False,
                   exog=None,
                   hold_back=None,
                   period=None,
                   missing='none',
                   *,
                   deterministic=None,
                   old_names=False)

No los explicaré uno por uno aquí, si quieres saber más al respecto, puedes ir a la explicación oficial:

modelos de estados.tsa.ar_model.AutoReg — modelos de estados

Por lo general, solo es necesario ingresar la secuencia endog y los retrasos de orden:

endog: acepta un tipo de matriz, una serie de tiempo unidimensional.

rezagos: orden del modelo, si es un número entero, el número de rezagos que se incluirán en el modelo o una lista de índices de rezagos que se incluirán. Por ejemplo, [1, 4] solo incluirá los retrasos 1 y 4, mientras que lags=4 incluirá los retrasos 1, 2, 3 y 4.

from statsmodels.tsa.ar_model import AutoReg
import numpy as np
 
# 生成N(0,1)随机正态分布（白噪声）
noise = np.random.randn(200)
wnoise = (noise-np.mean(noise))/np.std(noise)
 
# 生成AR(2)线性序列 X(t)=0.5X(t-1)+0.1X(t-2)
X = [20,10]  # 初值
for i in range(200):
    x2 = 0.5*X[i+1]+0.1*X[i]+wnoise[i]
    X.append(x2)
 
# 2阶AR模型拟合（OLS）
AR2_model = AutoReg(X, 2).fit()  
# 模型预测第3到第202个时间点的数据
predict = AR2_model.predict(2,201)  
# 计算残差
residual = X[2:]-predict

Después de simular y generar la carga lineal AR, realizamos un ajuste de orden AR2 para obtener el valor predicho y luego usamos matplotlib para mostrar:

import matplotlib.pyplot as plt
plt.figure()
plt.subplot(311)
plt.plot(X[2:])
plt.subplot(312)
plt.plot(predict)
plt.subplot(313)
plt.plot(residual)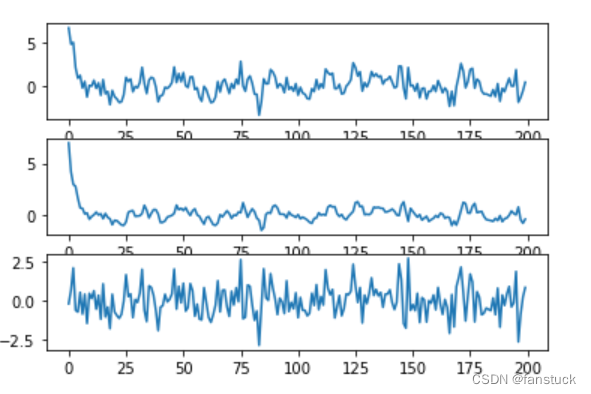

Preste atención, evite perderse, si hay algún error, deje un mensaje para recibir asesoramiento, muchas gracias.

Eso es todo por este tema. Estoy atascado. Si tiene alguna pregunta, no dude en dejar un mensaje para discutir. Nos vemos en la próxima edición.

ver

Conceptos relacionados de series temporales estacionarias

(51) Análisis de series temporales II: Análisis de series temporales estacionarias (ARMA)
Modelos MA y ARMA

Implementación en Python del modelo autorregresivo AR(p) [caso]_Noema_pku's blog-CSDN blog_python modelo autorregresivo

Análisis de series temporales: autorregresión (AR)

Creación de simios Convocatoria de ponencias｜Análisis de series temporales Algoritmos para predicción de series temporales estacionarias Algoritmos y modelos autorregresivos (AR) Explicación detallada + Implementación de código Python

prefacio

1. Algoritmo de pronóstico de series temporales estacionarias

1. Funciones de distribución, media y covarianza de series temporales

Distribuciones de probabilidad

función media

función de autocovarianza

función de autocorrelación

2. Funciones de autocovarianza y autocorrelación de series estacionarias

función de autocovarianza

función de autocorrelación

Propiedades de secuencias de autocovarianza y secuencias de función de autocorrelación para secuencias estacionarias

3. Series de tiempo estrictamente estacionarias

4. Amplia serie temporal estacionaria

5. Contacto y distinción

conectar

la diferencia

6. Secuencia de ruido blanco

definición

7. Secuencias IID

definición

En segundo lugar, el modelo autorregresivo (Modelo autorregresivo , denominado AR)

definición

Pasos de modelado

primer paso:

Paso 2:

tercer paso:

el cuarto paso:

Decisión modelo

Realización de casos

Preste atención, evite perderse, si hay algún error, deje un mensaje para recibir asesoramiento, muchas gracias.

ver

Supongo que te gusta