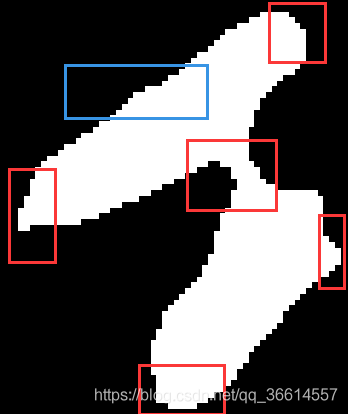
Dada una imagen de una región conectada, como se muestra en la figura a continuación, quiero solicitar la curvatura de sus píxeles de contorno.

En teoría, la curvatura de los píxeles de contorno en el cuadro rojo en la figura siguiente debería ser lo más grande posible, mientras que la curvatura del cuadro azul debería ser relativamente pequeña.
1. En primer lugar, la imagen se binariza y el contorno inicial (píxeles blancos) se obtiene mediante la extracción de bordes de cualquier operador:
I=im2bw(I);
eg=edge(I,'canny');
2. Pero puede haber un área determinada donde el "grosor" del contorno sea mayor que 1, lo que afectará la extracción de píxeles del punto del contorno posterior en orden, así que use bwmorph para refinar la imagen del contorno, por ejemplo:
eg=bwmorph(eg,'thin',Inf);Obtenga el esquema refinado:

3. El contorno refinado asegura que dentro de 8 vecindarios de un determinado píxel, haya y sólo otros dos puntos de contorno (uno es el píxel anterior a atravesar y el otro es el siguiente píxel a atravesar). Así que partimos de cualquier punto del contorno (sx, sy) y seguimos a lo largo de los píxeles no recorridos en la vecindad de 8 hasta que regresemos al punto de partida. Además del punto inicial, hay un solo píxel de vecindad para otros puntos , lo que asegura que el programa pueda comenzar desde el punto inicial correctamente y regresar al punto inicial después de atravesar todos los puntos.
Por lo tanto, definimos las matrices xey para almacenar las coordenadas xey de todos los píxeles atravesados en orden, y sx y sy son las coordenadas del punto atravesado actual. dir es la dirección de 8 vecindarios. Para el i-ésimo vecindario de (sx, sy), sus coordenadas son (sx + dir (i, 1), sy + dir (i, 2)). Defina un punto de búsqueda de función para averiguar si se ha atravesado el píxel de vecindad actual. Si el valor del píxel de vecindad es 1 (blanco) y no se ha atravesado, entonces sx, xy se actualizan a las coordenadas del píxel de vecindad y se almacenan en x, y. Para evitar entrar en un bucle infinito, se establece el estado f. Si los ocho píxeles vecinos no pueden cumplir la condición, significa que el final está roto, entonces se rompe directamente.
x=[];
y=[];
[sx,sy]=find(eg==1,1);%find the first point
x=[x,sx];
y=[y,sy];
dir=[[-1,-1];[-1,0];[-1,1];[0,1];[1,1];[1,0];[1,-1];[0,-1]];
while(true)
f=0;
for i=1:8
if eg(sx+dir(i,1),sy+dir(i,2))==1 && findpoint(x,y,sx+dir(i,1),sy+dir(i,2))
sx=sx+dir(i,1);
sy=sy+dir(i,2);
f=1;
break
end
end
if (f==0)%结束条件1:走到断头路 一般情况下不会满足
break
end
if(sx==x(1) && sy==y(1)) %结束条件2:走到起始点
break
end
x=[x,sx];
y=[y,sy];
endLa función findpoint devuelve 0 solo cuando sx y sy aparecen en el mismo índice de xy al mismo tiempo, lo que indica que el punto ha sido atravesado; de lo contrario, devuelve 1.
function f=findpoint(x,y,sx,sy)
n=length(x);
f=1;
for i=1:n
if x(i)==sx && y(i)==sy
f=0;
break;
end
end
end4. Las xey obtenidas de esta manera están conectadas a una matriz (lista / vector), y cada punto de las coordenadas x (i), y (i) será igual ax (i-1), y (i- 1) y x (i + 1) y y (i + 1) son adyacentes, por lo que la diferencia entre x (i) yx (i + 1) adyacentes se usa para aproximar la derivada en la dirección x, y y es la mismo. Por lo tanto, se obtiene la matriz de diferencias de primer orden (derivada) dfx1, dfy1; la diferencia de segundo orden (derivada) se puede operar sobre la base de la diferencia de primer orden (derivada) para obtener dfx2, dfy2.
dfx1=[diff(x,1),x(1)-x(end)];
dfy1=[diff(y,1),y(1)-y(end)];
dfx2=[diff(dfx1,1),dfx1(1)-dfx1(end)];
dfy2=[diff(dfy1,1),dfy1(1)-dfy1(end)];La diferencia adyacente se puede obtener directamente con diff, pero la diferencia del último punto se perderá y se puede complementar con x (1) -x (end).
5. La matriz de diferencias dfx1 (i), dfy (i) ahora obtenida representa la "derivada" de x (i) y y (i). Para mostrar visualmente la curvatura de cada punto en la imagen, mapeamos dfx1, etc. Para la matriz bidimensional dx1, etc., dfx1 (i, j), dfy (i, j) representan las "derivadas" de los puntos i, j.
dx1=zeros(m,n);
dx2=zeros(m,n);
dy1=zeros(m,n);
dy2=zeros(m,n);
for i=1:length(x)
dx1(x(i),y(i))=dfx1(i);
dy1(x(i),y(i))=dfy1(i);
dx2(x(i),y(i))=dfx2(i);
dy2(x(i),y(i))=dfy2(i);
end6. Calcule la matriz de curvatura K de acuerdo con la fórmula de curvatura:

K=zeros(m,n);
K=abs(dx1.*dx2-dx2.*dy1)./((dx1.^2+dy1.^2+0.1).^(3/2));Para evitar que el denominador sea 0, agregue 0.1 al denominador.
Dibuja la imagen de K directamente:

Cuanto más blanco sea el color, mayor será la curvatura, pero este resultado es muy insatisfactorio. La razón es que la diferencia entre puntos discretos se usa para aproximar la derivada de la curva continua y el error es demasiado grande (por ejemplo, usando (sin (1) -sin (0)) / (1-0) aproxima la derivada de sinx en x = 0, y obtiene 0.017, que es demasiado grande para la derivada real de 1). Por lo tanto, no es bueno calcular la derivada o la curvatura por el método de la diferencia adyacente.
Por lo tanto, intentamos usar x (i + 1) -x (i-1) en lugar de x (i + 1) -x (i) para aproximar la derivada de x (i) y y (i) en la dirección x :
dfx1=([diff(x,1),x(1)-x(end)]+[x(1)-x(end),diff(x,1)])/2;
dfy1=([diff(y,1),y(1)-y(end)]+[y(1)-y(end),diff(y,1)])/2;
dfx2=([diff(dfx1,1),dfx1(1)-dfx1(end)]+[dfx1(1)-dfx1(end),diff(dfx1,1)])/2;
dfy2=([diff(dfy1,1),dfy1(1)-dfy1(end)]+[dfy1(1)-dfy1(end),diff(dfy1,1)])/2;
Pero el resultado sigue siendo inobservable Parece que es imposible aproximar con precisión la derivada en puntos discretos (¿o intentar encontrar la diferencia de n puntos cercanos?), Especialmente en imágenes muy pequeñas. Imagine que la definición de curvatura parece ser lo opuesto a "rectitud", es decir, cuanto más cerca esté el punto cerca de este punto de píxel (aquí se refiere a continuo) a una línea recta, menor será la curvatura. Por el contrario, si se produce un giro, la curvatura debería ser mayor ¿No es un poco como una regresión lineal?
Por lo tanto, se adopta la idea de regresión lineal para calcular el grado de curvatura del segmento de línea compuesto por puntos cercanos a cada punto. Suponiendo que los puntos x (i) y y (i) son pre y el punto anterior, y hay un total de puntos siguientes después, entonces el segmento de línea se compone de puntos pre + siguiente + 1, y sus coordenadas son x ( i-pre: i + siguiente), y (i-pre: i + siguiente).
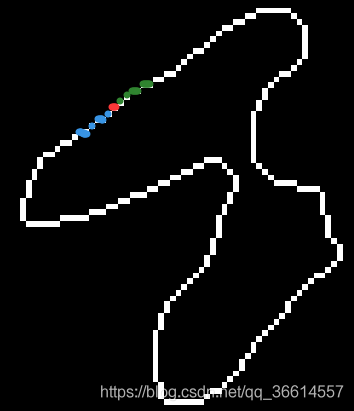
Por ejemplo, el punto actual está representado por rojo, el punto anterior está representado por verde y el siguiente punto está representado por azul. Después de la regresión lineal sobre ellos, la probabilidad de que no estén en línea recta, o el error de regresión y se pueden utilizar otros parámetros como valor de este punto. Tome las estadísticas (1) devueltas por la regresión como ejemplo. Cuanto más recta es la línea recta, más cerca están estas estadísticas (1) de 1, y viceversa. Por lo tanto, las estadísticas 1 (1) se utilizan aquí para indicar el grado de curvatura. La K obtenida tras sucesivos cálculos es:
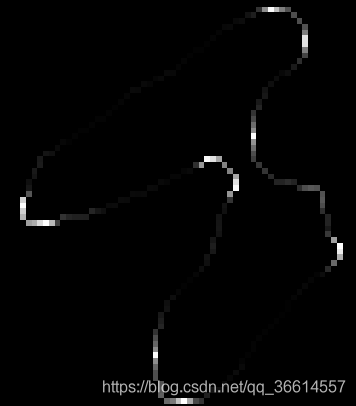
Los puntos blancos brillantes se distribuyen en las esquinas, lo que está bastante en línea con nuestros requisitos, OVER.
Código completo:
(Para evitar discutir el problema del valor crítico, el límite de xey se expande antes y después en la regresión lineal)
I=imread('平滑.jpg');
I=im2bw(I);
[m,n]=size(I);
eg=edge(I,'canny');
eg=bwmorph(eg,'thin',Inf);
x=[];
y=[];
[sx,sy]=find(eg==1,1);%find the first point
x=[x,sx];
y=[y,sy];
dir=[[-1,-1];[-1,0];[-1,1];[0,1];[1,1];[1,0];[1,-1];[0,-1]];
while(true)
f=0;
for i=1:8
if eg(sx+dir(i,1),sy+dir(i,2))==1 && findpoint(x,y,sx+dir(i,1),sy+dir(i,2))
sx=sx+dir(i,1);
sy=sy+dir(i,2);
f=1;
break
end
end
if (f==0)
break
end
if(sx==x(1) && sy==y(1))
break
end
x=[x,sx];
y=[y,sy];
end
%用线性回归类比曲率
pre=5;
next=5;
x=[x(end-pre+1:end),x,x(1:next)];
y=[y(end-pre+1:end),y,y(1:next)];
K=zeros(m,n);
for i=pre+1:length(x)-next
X=x(i-pre:i+next);
X=[ones(size(X')),X'];
Y=y(i-pre:i+next);
[b,bint,r,rint,stats]=regress(Y',X,0.05);
K(x(i),y(i))=1-stats(1);
end
%传统方式计算曲率的代码
% dx1=zeros(m,n);
% dx2=zeros(m,n);
% dy1=zeros(m,n);
% dy2=zeros(m,n);
% dfx1=[diff(x,1),x(1)-x(end)];
% dfy1=[diff(y,1),y(1)-y(end)];
% dfx2=[diff(dfx1,1),dfx1(1)-dfx1(end)];
% dfy2=[diff(dfy1,1),dfy1(1)-dfy1(end)];
%
% dfx1=([diff(x,1),x(1)-x(end)]+[x(1)-x(end),diff(x,1)])/2;
% dfy1=([diff(y,1),y(1)-y(end)]+[y(1)-y(end),diff(y,1)])/2;
% dfx2=([diff(dfx1,1),dfx1(1)-dfx1(end)]+[dfx1(1)-dfx1(end),diff(dfx1,1)])/2;
% dfy2=([diff(dfy1,1),dfy1(1)-dfy1(end)]+[dfy1(1)-dfy1(end),diff(dfy1,1)])/2;
%
% for i=1:length(x)
% dx1(x(i),y(i))=dfx1(i);
% dy1(x(i),y(i))=dfy1(i);
% dx2(x(i),y(i))=dfx2(i);
% dy2(x(i),y(i))=dfy2(i);
% end
%
% K=zeros(m,n);
% K=abs(dx1.*dx2-dx2.*dy1)./((dx1.^2+dy1.^2+0.1).^(3/2));
function f=findpoint(x,y,sx,sy)
n=length(x);
f=1;
for i=1:n
if x(i)==sx && y(i)==sy
f=0;
break;
end
end
end