Notas de lectura de "Principios de la red neuronal artificial" (4) - Red neuronal de propagación hacia atrás de error

Resumen de todas las notas: "Principios de las redes neuronales artificiales" -Resumen de las notas de lectura

1. La propuesta de red neuronal de retropropagación de error

Se utiliza una función de transformación continua no lineal para hacer que las neuronas de la capa oculta tengan capacidad de aprendizaje.

2. Estructura de la red neuronal de retropropagación de errores

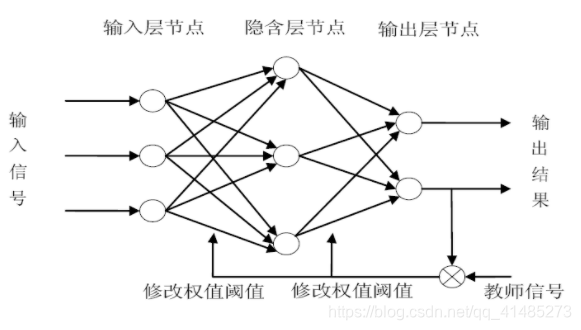
Estructura de interconexión

• La red neuronal de BP es una red directa con tres o más capas sin retroalimentación y sin interconexión en las capas. Las neuronas entre las capas están completamente conectadas y no hay conexión entre las neuronas en cada capa.

La red neuronal de BP utiliza un método de aprendizaje guiado para la formación y el aprendizaje.

El "algoritmo de aprendizaje de retropropagación de error" adoptado por la red neuronal BP es un método de aprendizaje en el que la función de error desciende según el gradiente.

3. Estructura de la unidad de procesamiento de la red neuronal de retropropagación de errores

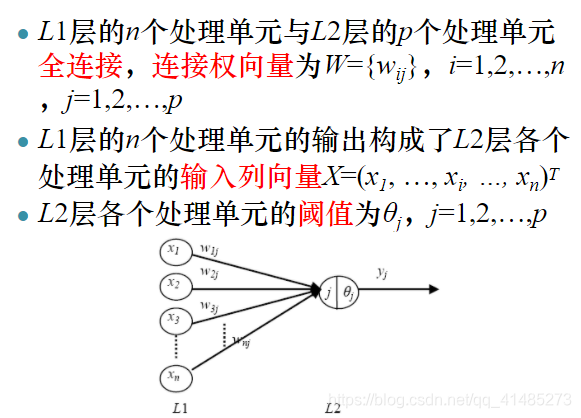
Cuatro, algoritmo de aprendizaje de retropropagación de errores

El proceso de aprendizaje de la red neuronal BP

• Extensión de modo
• Error de retropropagación
• Entrenamiento de la memoria
• Convergencia de aprendizaje

El problema mínimo local del algoritmo de aprendizaje de BP estándar Algoritmo de aprendizaje de BP

• Fenómeno
  Después de que el aprendizaje se ha llevado a cabo un cierto número de veces, aunque la salida real de la red y la salida esperada todavía tienen un gran error, no importa cómo se realice el aprendizaje, el error global de la red cambia lentamente, o ya no cambia en absoluto.
• La razón es que el
  algoritmo de aprendizaje de BP usa la función de error para aprender el algoritmo de acuerdo con el gradiente.
  
• Solución
  Cambie correctamente el número de unidades en la capa oculta de la red neuronal BP;
  agregue un pequeño número aleatorio a cada peso de conexión inicial.

Cinco, la base matemática del algoritmo de aprendizaje de propagación de la dirección del error

• Descenso de gradiente

En sexto lugar, la mejora del algoritmo de aprendizaje de retropropagación de errores.

Problemas con el algoritmo de BP

La velocidad de convergencia del algoritmo de aprendizaje es lenta.

• La tasa de aprendizaje afecta la velocidad de convergencia: si la tasa de aprendizaje es demasiado pequeña, la red convergerá lentamente; si la tasa de aprendizaje es demasiado grande, la red oscilará y no convergerá.
• Por lo general, el rango de valores de la tasa de aprendizaje es $0.01\sim 1$。

Mínimos locales

• Este problema se puede evitar en la medida de lo posible estableciendo un valor inicial más pequeño del peso de la conexión.

La selección del número de capas ocultas y el número de nodos carece de orientación teórica.

Existe una tendencia a olvidar muestras antiguas cuando se aprenden nuevas muestras durante el entrenamiento.

Algoritmo de corrección de errores acumulativos

Idea básica

• Calcular mmSuma de errores acumulativos de$m$ pares de modos de aprendizaje$mi={\sum }_{k=1}^m{mi}^k$

Comparación del algoritmo BP y el algoritmo BP para la corrección de errores acumulativos

• En el algoritmo BP de corrección de errores acumulativos, el número de correcciones para cada peso y umbral de conexión se reduce significativamente (cada aprendizaje reduce $metro-1$ corrección de tiempo), lo que reduce el tiempo de aprendizaje, especialmente cuando el modo de aprendizaje es menor, la velocidad de convergencia del error acumulativo del algoritmo BP es más rápida que el algoritmo BP.
• El algoritmo de BP de error acumulativo se basa en mmEl error acumulativo de los pares de modos de aprendizaje$m$ y el ajuste de los pesos de conexión pueden promediar fácilmente los errores de cada modo de aprendizaje y causar fácilmente oscilaciones de la red.

Salida de función sigmoidea que limita el algoritmo de PA

Idea básica

• El ajuste del peso de la conexión está relacionado con la salida de la capa oculta. Cuando la salida de la capa oculta es 0 o 1, la cantidad de corrección del peso de conexión $\Delta w_{ij}$Y $\Delta v_{jt}$Si es 0, no hay efecto de corrección.
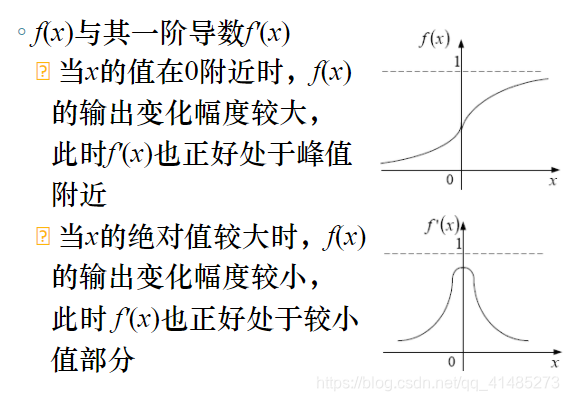
• La salida de la capa oculta está determinada por la salida de la función Sigmoide.
• La función sigmoidea tiene características de salida no lineales saturadas
  cuando $X<-5$ ,$f(x)\; está$ cerca de 0;
  cuando$X>+5$ ,$f(x)\; está$ cerca de 1;
  cuando$Cuando\; x$ está cerca de 0 ($-5\le X\le 5$） ，$f\left(x\right)$ realmente juega el papel de transferencia.

Algoritmo de limitación de la función sigmoidea

IF f(x)<=0.01
THEN
	f(x)=0.01
else
	IF f(x)>=0.99
	THEN
		f(x)=0.99
	ELSE
		f(x)保持不变

Algoritmo de BP para aumentar el plazo de impulso

Cuando el algoritmo de PA estándar ajusta los pesos de conexión, solo considera la dirección del descenso del gradiente de error durante este ajuste, pero no considera la dirección del gradiente de error durante el ajuste anterior, por lo que el proceso de entrenamiento a menudo oscila y la convergencia es lenta.

Idea básica

• Cuando se ajusta el peso de conexión, la cantidad de ajuste del aprendizaje anterior, es decir, el término de impulso, se suma de acuerdo con una cierta proporción, en un esfuerzo por hacer que el ajuste del peso de conexión se realice en la misma dirección.
• El elemento variable hace que el ajuste del peso de conexión cambie gradualmente a lo largo de la dirección promedio a medida que cambia el proceso de entrenamiento. $$\Delta W_{ij}\left(n\right)=-\beta \cdot \frac{\partial E}{\partial W_{ij}}+\eta \left(n\right)\cdot \Delta W_{ij}(n-1)$$

Algoritmo de PA de ajuste adaptativo de la tasa de aprendizaje

Idea básica

• La tasa de aprendizaje es uno de los factores clave que afectan el algoritmo de aprendizaje de BP y debe ajustarse constantemente durante el proceso de entrenamiento.
• Si el error sigue disminuyendo y tiende al objetivo, significa que la dirección de corrección del error es correcta y la tasa de aprendizaje se puede aumentar; si el error sigue aumentando y excede el valor preestablecido, significa que la dirección de corrección del error es incorrecta, y el La tasa de aprendizaje debe reducirse en este momento.
• $K_{inc}$Es el factor de incremento de la tasa de aprendizaje, $K_{dec}$¿Es el factor de disminución de la tasa de aprendizaje $$\alpha (n+1)=\{\begin{array}{l}{K}_{inc}\cdot \alpha \left(n\right)E(n+1)<E\left(n\right)\\ \\ K_{dec}\cdot \alpha \left(n\right)E(n+1)\ge E\left(n\right)\end{array}$$

Siete, la función de extracción de características de la capa oculta

La capa oculta también se denomina capa de extracción de características.

Cada neurona de la capa oculta tiene la capacidad de extraer características de diferentes patrones de entrada y transferir las características extraídas a la capa de salida.

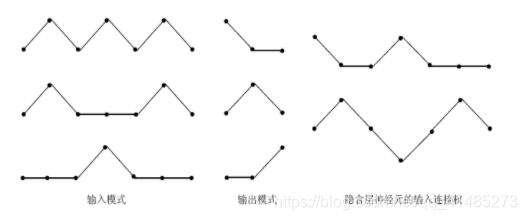
Ocho, la principal capacidad de la red neuronal de retropropagación de errores.

• Capacidad de mapeo no lineal
• Generalización
• Tolerancia a fallos

El próximo capítulo Portal: "Principios de las redes neuronales artificiales" Notas de lectura (5) -Red neuronal Hopfield