Tabla de contenido
El blog anterior implementó un paquete aritmético de enteros grandes (Java) (1): suma, resta, multiplicación, división, modo módulo, suma modular (considerada negativa) , nos dimos cuenta de la gran cantidad de suma básica, resta, multiplicación, Dividir, tomar el resto. Este blog se basará en ellos para lograr módulo de potencia rápido , máximo común divisor , elemento inverso multiplicativo , determinación de números primos y generación de números primos grandes .
1. Módulo de potencia rápido
Si queremos calcular 2100 mod 19, la forma más sencilla es hacer 99 multiplicaciones y luego módulo 19.
Pero esto tendrá dos problemas: 1. Llevará mucho tiempo multiplicar todo el tiempo; 2. El número eventualmente se volverá muy grande y difícil de almacenar,
por lo que usaremos una exponenciación rápida (similar al método binario), por lo que contamos 7 Eso es.
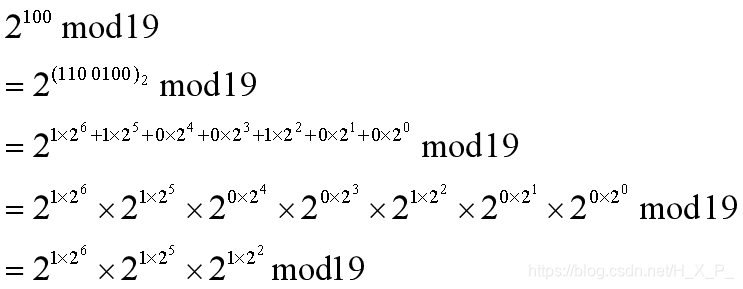
Entre ellos, también usaremos las siguientes dos fórmulas, para que el número que obtengamos no sea muy grande.
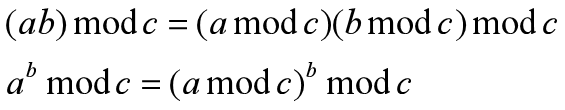
/**
* 快速幂取模
* @param one 底数
* @param two 指数
* @param mod 模
* @return 结果
*/
public static String Power(String one,String two,String mod) {
if(two.equals("0")) {
//0次幂结果为1
//System.out.println("Power result=1");
return "1";
}else if(two.equals("1")){
//1次幂结果为它本身
return Mod(one, mod);
}
String count=two,result="1",temp=one;
while(!count.equals("0")){
if(Mod(count, "2").equals("1")) //看它二进制最后一位是不是1
result=Multiply(result, temp, mod);
if(!count.equals("1")) //这里避免最后一次做没用的乘法
temp=Multiply(temp, temp, mod);
count=Division(count, "2"); //次数减1,相当于二进制右移一位
}
//System.out.println(result);
return result;
}
Resultado de la operación:
2 5 mod 7 = 4
2 10 mod 13 = 10
2 100 mod 19 = 17
2 1000 mod 1777 = 1,775
2 10,000 mod 49999 = 100
2 100 000 mod 998 111 = 802 658
En segundo lugar, el máximo común divisor (algoritmo euclidiano)
Puede usar el algoritmo de Euclides para encontrar el máximo común divisor, también conocido como método de lanzar y dividir.
Ahora encuentre el máximo común divisor de 52 y 36:
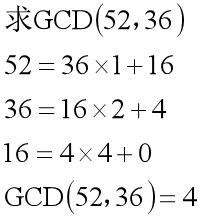
cuando el resto es 0, el divisor de la fórmula actual es el máximo común divisor.
/**
* 最大公约数
* @param one
* @param two
* @return 结果
*/
public static String GCD(String one,String two) {
if(one.equals(two)) {
//相等则GCD=任意一个
//System.out.println("GCD="+one);
return one;
}
int length1=one.length();
int length2=two.length();
String first=null,second=null,temp=null;
if(length1>length2) {
//保证第一个数大于第二个,当然也可以不用这么做
first=one;
second=two;
}else if(length1<length2) {
first=two;
second=one;
}else {
for (int i = 0; i < length1; i++) {
if(one.charAt(i)>two.charAt(i)) {
first=one;
second=two;
break;
}
else if(one.charAt(i)<two.charAt(i)) {
first=two;
second=one;
break;
}
}
}
while(!second.equals("0")) {
temp=Mod(first, second);
first=second;
second=temp;
}
//System.out.println("GCD="+first);
return first;
}
Tres, elemento inverso multiplicativo (algoritmo euclidiano extendido)
Si ab≡1 mod p y MCD (a, p) = 1 (a y p son primos relativos), entonces el inverso multiplicativo de a con respecto al módulo p se llama b.
Ahora use el algoritmo euclidiano extendido para encontrar el inverso multiplicativo de 15 módulo 41:

/**
* 扩展欧几里得算法
*/
static String x= "0",y= "0";
public static String ExtendGCD(String a,String b) {
if(b.equals("0")) {
Operation.x="1";
Operation.y="0";
return a;
}
String d=ExtendGCD(b, Mod(a, b));
String temp=Operation.x;
Operation.x=Operation.y;
Operation.y=Subtract(temp, Multiply(Division(a, b), Operation.y));
//System.out.println(" "+Operation.x);
//System.out.println(" "+Operation.y);
return d;
}
/**
* 乘法逆
* @param a
* @param mod
* @return
*/
public static String MultiplicativeInverse(String a,String mod) {
String d=ExtendGCD(a,mod);
if(d.equals("1"))
return Add(Mod(Operation.x, mod), mod, mod);
return "-1"; //没有逆元
}
Resultado de la operación:
5 módulo 23 elemento inverso multiplicativo = 14
28 módulo 75 elemento inverso multiplicativo = 67
83 módulo 108 elemento
inverso multiplicativo =
95119 módulo 4399 elemento inverso multiplicativo = 1109 49999 módulo 1234567 elemento inverso multiplicativo = 1078243
Cuarto, la determinación de números primos (algoritmo de Miller Robin)
Descripción del algoritmo de Miller-Robin: el algoritmo para

juzgar si un número es primo o no es aproximadamente el siguiente:


aquí quiero decir que si el algoritmo de módulo de potencia en el algoritmo no se selecciona correctamente, todo el algoritmo de Miller-Robin tomará un tiempo aterrador ...
/**
* 米勒罗宾算法
* @param one
* @return
*/
public static boolean MillerRabin(String one) {
if(one.equals("0")||one.equals("1")) //0和1不是素数
return false;
if(one.equals("2")) //2是素数
return true;
if((one.charAt(one.length()-1)-48)%2==0) //偶数不是素数
return false;
String number=Subtract(one, "1"); //计算n-1
String number1=number;
int count=0;
while((number1.charAt(number1.length()-1)-48)%2==0) {
//n-1=m*2^t
number1=Division(number1, "2");
count++;
}
for(int i=1;i<=5;i++) {
//(a^(n-1))%n=(a^(m*2^t))%n
String random=String.valueOf(i+2);
String x=Power(random, number, one); //(a^m)%n
String y="";
for(int j=1;j<=count;j++) {
//((a^m)^(2^t))%n
y=Multiply(x, x, one);
if(y.equals("1")&&!x.equals("1")&&!x.equals(number)) //如果不满足二次探测定理,则不是素数
return false;
x=y;
}
if(!y.equals("1")) //如果不满足费马小定理,则不是素数
return false;
}
return true;
}
Resultado de la operación:
111561511 es un número compuesto
564765326677 es un número primo
49841516591656517 es un número compuesto
555469971929450687843 es un número primo
262314699260834231863164359738235486290658375509 es un número primo
89220925196820658375509 es un número primo
Cinco, gran número primo generado

/**
* 生成素数算法
* @return 素数
*/
public static String PrimeGeneration() {
//一般来说,整除100以内的所有素数可排除76%不是素数的可能性,整除256以内的所有素数可排除80%
//不是素数的可能性,所以创建小素数表,可以大幅加快速度,当然这个表可以手动生成
String[] table= {
"3","7","11","13","17","19","23","29","31","37","41","43","47",
"53","59","61","67","71","73","79","83","89","97","101","103","107","109",
"113","127","131","137","139","149","151","157","163","167","173","179",
"181","191","193","197","199","211","223","227","229","233","239","241",
"251","257","263","269","271","277","281","283","293","307","311","313",
"317","331","337","347","349","353","359","367","373","379","383","389",
"397","401","409","419","421","431","433","439","443","449","457",
"461","463","467","479","487","491","499"};
Random random=new Random();
int flag;
long time1=System.currentTimeMillis();
while(true) {
String number="";
for(int i=1;i<=33;i++) //生成一个随机的大奇数,这个位数任意取
number+=String.valueOf(random.nextInt(899999998)+100000001);
System.out.println(number);
int num=random.nextInt(800)+101; //后三位
if(num%2==0) //跳过偶数
num++;
for(int i=1;i<=50;i++,num+=2) {
//搜索附近的50个奇数
String temp="";
if(num%5==0) //跳过5的倍数
num+=2;
temp=temp+number+String.valueOf(num);
flag=0;
for(int j=0;j<table.length;j++) {
if(Mod(temp, table[j]).equals("0")) {
//看能不能被小整数整除
flag=1;
break;
}
}
if(flag==1)
continue;
else
if(MillerRabin(temp)) {
//米勒罗宾算法
System.out.println("素数: "+temp);
System.out.println("时间差="+(System.currentTimeMillis()-time1)+"ms");
return temp;
}
}
}
}
Resultados de la operación (300 decimal generar grandes números primos):
955042930633410289133616296687431777269353980956568253574985061454859846383784618868936295454149058329055354262839296541908590329891268218404276396709186373481902442299599349413886590143757678944807286223232776732690994758060943148907454012806238319657554857310557054678934303822406793932126613431907 es primo
369529ms de diferencias de tiempo =
886561163228838664750509032768759020351470065461506216295171421466522603290150530199373404129571069480539452635354057998985307892246327624821492158196842621382357442511837684610582698182410676560942977011624164506742932167839443913503332061016760221262755081522835308001246894308971214499396769460513 es primo
Diferencia de tiempo = 29439ms
214870052980815367577291784627902708719802277128149369356311939236596853366271103968812931332145864571367016263259506949201985903708991330657005820918132219051420306215369688007649436101361885347977415827831904465125972681277283243530766501893543832374257674319643447978284232131374047798140761172317 es primo
143827ms de diferencia horaria
Para los números primos grandes generados, podemos usar el algoritmo Miller Robin que escribimos anteriormente para detectar. Por supuesto, también puede usar la clase BigInteger de Java para juzgar (use esta clase para generar números primos grandes muy rápidamente, si está interesado, puede estudiarlo)
String string="955042930633410289133616296687431777269353980956568253574985061454859846383784618868936295454149058329055354262839296541908590329891268218404276396709186373481902442299599349413886590143757678944807286223232776732690994758060943148907454012806238319657554857310557054678934303822406793932126613431907";
BigInteger a=new BigInteger(string);
if(a.isProbablePrime(1024)) a是素数的概率为1 - 1 / 2^1024
System.out.println("素数");
else
System.out.println("合数");
Resultado de la operación: número primo