1. Definición:
enGráfico conectado no dirigidoG(V,E)Encuentre un Esubconjunto acíclico de aristas en T, de modo que pueda conectar todos los nodos y tenga el menor peso.
una)Dado que T es acíclico, puede considerarse como un árbol;
B)Dado que es generado por el gráfico G, se llama (gráfico G) árbol de expansión;
C)Dado que T tiene el peso más pequeño, se llama árbol de expansión mínimo.
Como T es acíclico, los vértices V deben tener aristas V-1.
2. Estrategia codiciosa:
cada vez que se cultiva un borde del árbol de expansión mínimo, se realizan ciclos V-1 para completar la construcción del árbol. Los bordes de crecimiento deben ser bordes livianos (peso mínimo) y no formar un anillo.
Método: algoritmo kruskal (Kruskal) o algoritmo prim (primo)
3. Algoritmo prim (primo):
Este algoritmo puede denominarse método de suma de puntos, cada iteración selecciona el punto correspondiente a la arista con el menor costo y lo agrega al árbol de expansión mínimo. El algoritmo comienza desde cualquier vértice sy crece gradualmente hasta cubrir todos los vértices de todo el gráfico conectado.
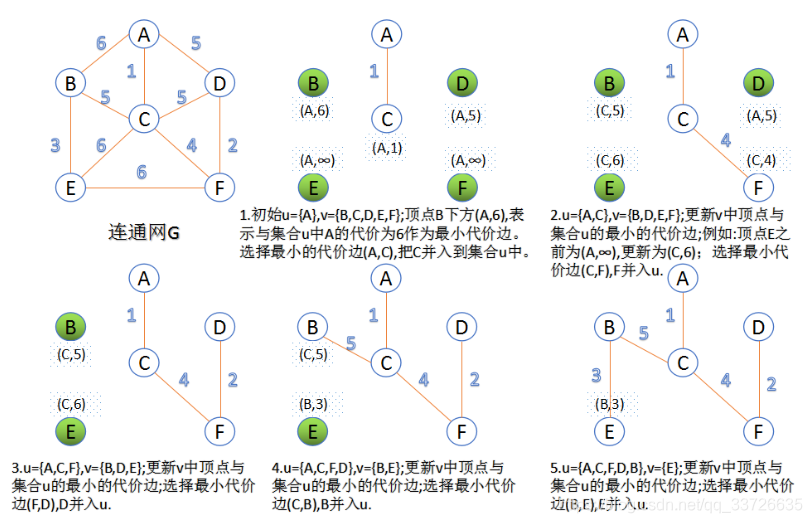
3.1. Flujo y gráfico del algoritmo:
Entrada: gráfico G(V,E)y cualquier nodo ucomo punto de partida; salida: conjunto de bordes P
- El nodo se
uune a la colección de nodosU; - Seleccione el
Uborde de menor costo conectado a los nodos en el conjunto para unir el conjuntoP(como los bordes<u,v>) yvuna los nodos conectados (como ) al conjuntoU;
(si hay varios bordes con el mismo peso, puede elegir uno de ellos a voluntad); - Repita el paso 2 hasta que todos los nodos se unan al conjunto
U.
3.2. Código C ++:
#include <queue>
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
struct edge {
// 边的定义
int start;
int end;
int weight;
edge(int x, int y, int z) :start(x), end(y), weight(z) {
}
bool operator< (const edge& tmp) const {
//用于优先队列的比较函数
return weight > tmp.weight;
}
};
const int NUM = 6;
int G[NUM][NUM]; //假设图已经定义好了,如G[0][2] = 5; 5为权重
void MiniSpanTree_prim(int(*G)[NUM], int root)
{
vector<int> V; //记录MST已经包含的点;
V.push_back(root);
priority_queue<edge> edge_all; // 放入权重边,自动排序
for (int i = 0; i < NUM; i++) {
// 放入与起点连接的边
if (G[root][i] != 0) {
// 0 代表没有路
edge tmp(root, i, G[root][i]);
edge_all.push(tmp);
}
}
cout << "Prim :" << endl;
for (int i = 0; i < NUM - 1; i++) {
//共N-1条边
edge curr = edge_all.top(); //取得代价最小边
edge_all.pop();
while (find(V.begin(), V.end(), curr.end) != V.end()) {
//边终点若已包含,则丢弃后换一条边
curr = edge_all.top();
edge_all.pop();
}
V.push_back(curr.end); //放入这条边的终点v
cout << curr.start << " --> " << curr.end << " " << curr.weight << endl; // 输出MST的边
for (int j = 0; j < NUM; j++) {
// 加入终点v连接的边
if (G[curr.end][j] != 0 && find(V.begin(), V.end(), j) == V.end()) {
edge tmp(curr.end, j, G[curr.end][j]);
edge_all.push(tmp);
}
}
}
}
4. Algoritmo de Kruskal (Kruskal):
este algoritmo se puede llamar el método de borde aditivo . El número de borde del árbol de expansión mínimo inicial es 0. Cada iteración selecciona un borde de costo mínimo que satisface la condición y lo agrega al conjunto de bordes del árbol de expansión mínimo en.
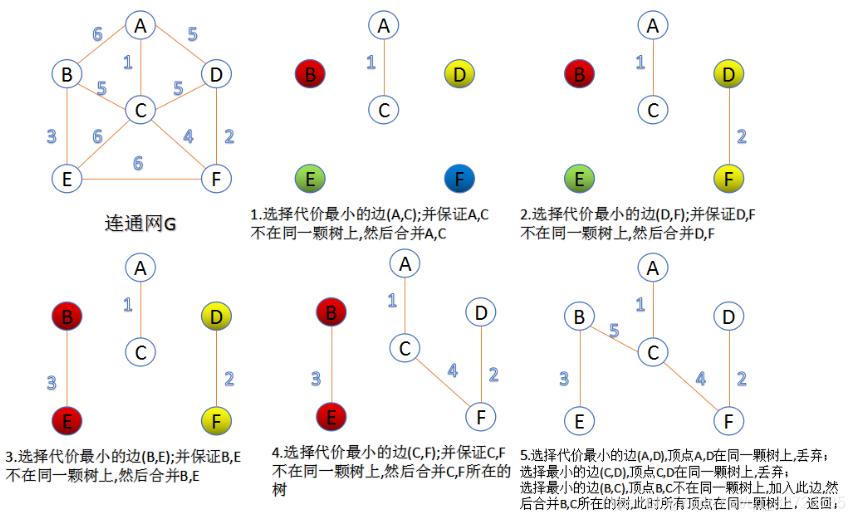
4.1. Diagrama y flujo del algoritmo:
entrada: gráfico G(V,E); salida: conjunto de bordes P.
- Ordene todas las aristas en el gráfico de menor a mayor costo;
- Considere los n vértices del gráfico como un bosque de n árboles independientes;
- Seleccione los bordes de menor a mayor peso,
u,vSi los dos vértices del borde seleccionado pertenecen a dos árboles diferentes, se convierten en un borde del árbol de expansión mínimo y los dos árboles se fusionan en un árbol al mismo tiempo. De lo contrario, tome el borde con el peso más pequeño y vuelva a intentarlo. - Repita (3) hasta que todos los vértices estén en un árbol o haya n-1 aristas.
4.2. Código C ++:
#include <queue>
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
struct edge {
// 边的定义
int start;
int end;
int weight;
edge(int x, int y, int z) :start(x), end(y), weight(z) {
}
bool operator< (const edge& tmp) const {
//用于优先队列的比较函数
return weight > tmp.weight;
}
};
const int NUM = 6;
int G[NUM][NUM]; //假设图已经定义好了,如G[0][2] = 5; 5为权重
void MiniSpanTree_kruskal(int(*G)[NUM])
{
int node_coll[NUM] = {
0 }; //判断节点是否属于一棵树
int count = 1; // 用于不同树的标记
priority_queue<edge> edge_all; // 放入权重边,自动排序
for (int i = 0; i<NUM; i++) {
//放入所有边,并自动排序
for (int j = 0; j<NUM; j++) {
if (G[i][j] != 0) {
edge tmp(i, j, G[i][j]);
edge_all.push(tmp);
}
}
}
for (int i = 0; i<NUM - 1; i++) {
//共N-1条边
edge tmp = edge_all.top(); // 取代价最小边
edge_all.pop();
while (node_coll[tmp.start] == node_coll[tmp.end] && node_coll[tmp.start] != 0 && node_coll[tmp.end] != 0) {
// 找到属于不同树的边
tmp = edge_all.top();
edge_all.pop();
}
cout << tmp.start << " --> " << tmp.end << " " << tmp.weight << endl; // 输出MST的边
if (node_coll[tmp.start] == 0 && node_coll[tmp.end] == 0) {
//不同树的边的情况1
node_coll[tmp.start] = count;
node_coll[tmp.end] = count;
count++;
}
else if (node_coll[tmp.start] == 0 && node_coll[tmp.end] != 0) {
//不同树的边的情况2
node_coll[tmp.start] = count;
node_coll[tmp.start] = node_coll[tmp.end];
}
else if (node_coll[tmp.start] != 0 && node_coll[tmp.end] == 0) {
//不同树的边的情况3
node_coll[tmp.start] = count;
node_coll[tmp.end] = node_coll[tmp.start];
}
else if (node_coll[tmp.start] != 0 && node_coll[tmp.end] != 0) {
//不同树的边的情况4
node_coll[tmp.start] = count;
for (int i = 0; i<NUM; i++) {
if (node_coll[i] = node_coll[tmp.end]) {
node_coll[i] = node_coll[tmp.start];
}
}
}
}
}
Material de referencia: Dos métodos de árbol de expansión mínimo (algoritmo de Kruskal y algoritmo Prim)
Introducción al algoritmo 23.2 Algoritmo de Kruskal y algoritmo de Prim
para resumir:
1. El algoritmo kruskal es el método de suma, el algoritmo prim es el método de suma y la idea del algoritmo de memoria es buena.